Негізгі түсініктер және анықтамалар

ЛЕКЦИЯ. Негізгі түсініктер және анықтамалар. Айнымалылары ажыратылатын теңдеулер

Лекция мақсаты: Дифференциалдық теңдеулердің негізгі түсініктерімен студенттерді таныстыру.

Негізгі сөздер: теңдеу реті, интегралдық қисық, векторлар өрісі, изоклина, шешімдер.

Ысқаша мазмұны

Негізгі түсініктер және анықтамалар

Дифференциалдық теңдеу деп тәуелсіз айнымалыны, белгісіз функцияны және оның туындыларын байланыстыратын теңдікті атайды. Егер белгісіз функция тек бір ғана тәуелсіз айнымалыдан тәуелді болса, ондай теңдеуді жәй дифференциалдық теңдеу деп, ал бірнеше аргументтен тәуелді болса, ондай теңдеуді дербес туындылы дифференциалдық теңдеу деп атайды. Теңдеуге кіретін туындылардың ең жоғарғы реті дифференциалдық теңдеудің реті деп саналады.

Жәй дифференциалдық теңдеудің туынды бойынша шешілмеген түрі мынадай қатынаспен беріледі:

(1)

Мұндағы, 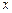-тәуелсіз айнымалы, 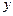-белгісіз функция, ал - оның туындылары.

Әдетте, теңдеудің ең жоғарғы реттегі туындысы бойынша шешілген түрі қарастырылады. Ол былай жазылады:

(2)

Дербес туындылы дифференциалдық теңдеулерді тәуелсіз айнымалылардың санына байланысты әртүрлі етіп жаза беруге болады. Солардың ішінен екі тәуелсіз айнымалыға байланысты түрін мына түрде жазуға болады:

(3)

Мұндағы, – тәуелсіз айнымалылар, 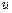- белгісіз функция, ал - дербес туындылар.

Егер белгісіз функциялар бірнешеу болса, онда сол функциялар санына байланысты дифференциалдық теңдеулер жүйесі қарастырылады.

Дифференциалдық теңдеулердің шешімін табуды интегралдау деп атайды.

Жәй дифференциалдық теңдеудің шешімінің жазықтықтағы графигін интегралдық қисық деп атайды. Дербес туындылы дифференциалдық теңдеудің шешімінің кеңістіктегі геометриялық кескінін интегралдық бет деп атайды.

1.2. Біз бұл тарауда бірінші ретті жәй дифференциалдық теңдеулерді қарастырамыз және осы теңдеудегі тәуелсіз айнымалыны нақты деп есептейміз. Мұндай теңдеудің туынды бойынша шешілмеген түрі төмендегі қатынаспен жазылады:

(4)

Мұнда х -тәуелсіз айнымалы, –белгісіз функция, -туынды, ал F -берілген функция. Осы теңдеудің туынды бойынша шешілген түрі былай жазылады:

(5)

Мұндағы, -жазықтықтағы кейбір D облысында үздіксіз бірмәнді анықталған функция деп есептелінеді.

Нақты сандар осінде -аралығын қарастырайық. Бұл аралық тұйық та, ашық та, ақырлы немесе ақырсыз да болуы мүмкін. Соңғы жағдайда болуы мүмкін.

Анықтама-1. аралығында анықталған функциясы (5) теңдеудің шешімі деп аталады, егер ол мынандай үш шартты қанағаттандырса:

1) функциясы аралығының барлық нүктесінде

дифференциалданатын болса;

2) ;

3) .

Ескерту-1. Егер аралығы тұйық немесе жартылай тұйық

болса, онда шешімнің сәйкес оңжақтық немесе солжақтық туындылары бар болуы шарт.

Ескерту-2. функциясы D облысында үздіксіз болғандықтан, функциясы аралығында үздіксіз болады.

Ескерту-3. Шешімнің анықталу облысының байланысты жиын

болуы қажетті шарт.

Мысалы, функциясы теңдеуінің шешімі бола алмайды, өйткені болғанда анықталмаған. Бұл жерде D облысы бүкіл ХОУ жазықтығы бола тұрып, екінші шарт орындалмайды. Бірақ, функциясы және аралықтарында шешім болады.

Кейбір жағдайларда (5) теңдеумен қатар оның аударылған түрі де қарастырылады:

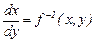(6)

Бұл теңдеу функциясы D облысының кейбір нүктесінің жақын аймағында шексіздікке айналып жататын жағдайда қарастырылады.

Егер шексіздікке ешқандай нүктеде жақындамаса, онда (5) және (6) теңдеулердің шешімдері, яғни олардың интегралдық қисықтары бір болады. Бұдан шығатын қорытынды: (5) теңдеудегі айнымалы х және у -тің кез келгенін тәуелсіз айнымалы деп қарастыруға болады да, екіншісін соған тәуелді функция деп алуға болады.

Сондықтан көп жағдайда (5) теңдеуді оның симметриялық түрінде жазады:

M(x,y)dx+N(x,y)dy=0 (7)

Мұндағы M(x,y) және N(x,y) функцияларын кейбір D облысында анықталған және үздіксіз деп есептейміз. Егер D облысындағы бір (х₀,у₀) нүктесінде

M(х₀,у₀)=N(х₀,у₀)=0 (8)

болса, онда ол нүктені ерекше нүкте деп атайды.

(7) теңдеуді (5) және (6) түрге келтірсек:

немесе (9)

түрінде жазамыз. Ал соңғы (9) қатынасты мына түрде жазуға болады:

. (10)

Осы (10) теңдеуді де дифференциалдық теңдеудің симметриялық түрі деп атайды.

1.3. Дифференциалдық теңдеудің шешімдері әдетте кез келген тұрақты санға байланысты болады. Сондықтан да дифференциалдық теңдеудің шешімдері шексіз жиын құрайды. Мысалы, теңдеуінің шешімін түрде жазуға болады. Мұндағы, С – кез келген тұрақты сан. Осы С санын өзгерте отырып, әртүрлі параболалар жиынын аламыз.

Практикалық есептерді шешкенде теңдеудің барлық шешімдерін табу емес, белгілі бір шарттарды қанағаттандыратын шешімді табу талап етіледі. Осындай есептің бір түрі Коши есебі деп аталады. Ол былай қойылады: берілген (5) теңдеудің барлық шешімдерінің арасынан тәуелсіз айнымалының берілген мәнінде берілген у₀ мәнін қабылдайтын, яғни

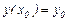(12)

шартын қанағаттандыратын шешімін табу керек. Қысқаша бұл есепті былай жазады:

(13)

Мұндағы, сандарын бастапқы мәндер, ал (12) теңдікті бастапқы шарт деп атайды. Осыған байланысты Коши есебін бастапқы есеп дейді.

Коши есебіне геометриялық түсініктеме беруге болады: (5) теңдеудің барлық интегралдық қисықтарының ішінен белгілі бір нүктесі арқылы өтетінін табу керек.

Егер (5) теңдеудегі тәуелсіз айнымалы 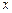-ты уақыт деп есептесек, ал теңдеудің шешімі кейбір М нүктесінің қозғалыс заңын өрнектейді десек, онда Коши есебіне механикалық түсінік беруге де болады: барлық қозғалыстардың ішінен бастапқы уақытта белгілі бір қалыпта тұрған нүктенің кейінгі қозғалысын табу керек.

Коши есебінің мақсаты берілген шартты қанағаттандыратын бір шешімді табу болғандықтан, ол есептің шешімі қай кезде бар және жалғыз болады деген сұрақтың тууы орынды. Бұл сұраққа жауап беретін теоремаларды келесі бір бөлімде келтіреміз.

Жоғарыда айтылғандай, дифференциалдық теңдеуді интегралдау нәтижесінде кез келген тұрақты саннан тәуелді функция аламыз:

(14)

Мұндай шешімдер жиынтығын жалпы шешім деп атайды. Жалпы алғанда (14) қатынастан кез келген Коши есебінің шешімін таба аламыз. Ол үшін бастапқы мәндерге сәйкес келетін С санын табу керек болады. Осы мақсатпен жалпы шешімнің төмендегідей анықтамасы қабылданған.

Анықтама-2. Айталық, 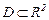облысы (5) теңдеудің Коши есебі шешімінің жалғыздық шарты орындалатын облыс болсын. Өзінің аргументтерінің кейбір облысында анықталған және х бойынша үздіксіз дифференциалданатын (14) функция (5) теңдеудің жалпы шешімі деп аталады, егер ол төмендегідей екі шартты қанағаттандырса:

1) D облысында (14) теңдік С саны бойынша шешілсе, яғни

(15)

2) тұрақты санның (15) өрнекпен анықталған кез келген мәнінде (14) функция (5) теңдеудің шешімі болса.

Бұл анықтамадан Коши есебінің кез келген бастапқы мәнді қанағаттандыратын шешімін табуға болады. Шынында да, жалпы шешім (14) өрнекке бастапқы және сандарын қойсақ, онда

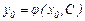
теңдігін аламыз. Анықтама бойынша бұл өрнек С саны бойынша шешіледі: . Осы табылған мәнді бастапқы (14) қатынасқа қойсақ,

өрнегін аламыз. Бұл іздеген шешіміміз болады.

Егер (14) өрнектің орнына мынадай қатынасты

(16)

алсақ, мұндағы - берілген тұрақты сан деп, ал -ты кез келген сан деп ұйғарсақ, онда (16) қатынасты Коши түріндегі жалпы шешім деп атайды.

Кез келген нүктесінде Коши есебінің жалғыздық шарты орындалатын шешім дербес шешім деп аталады да, кез келген нүктесінде жалғыздық шарты орындалмайтын шешім ерекше шешім деп аталады. Ерекше шешімнің кез келген нүктесі арқылы кем дегенде екі шешім өтеді. Дербес және ерекше шешімдерді басқаша да анықтауға болады: жалпы шешімдегі кез келген тұрақты С санының белгілі бір мәніндегі шешімді дербес шешім деп, ал сол санның кез келген шектелген немесе шексіз мәндерінде алынбайтын шешімді ерекше шешім деп атайды.

Дифференциалдық теңдеуді интегралдағандағы жалпы шешім айқындалмаған түрде алынатын болса, яғни

(17)

түрінде берілсе, онда осы (17) өрнекті теңдеудің жалпы интегралы деп атайды.

Егер соңғы қатынас

(18)

түрінде берілсе, ондағы функциясы теңдеудің интегралы деп аталады да, (18) қатынас теңдеудің бірінші интегралы деп аталады. Осындағы функциясының бір қасиетін айта кету керек: белгісіз у -тің орнына берілген (5) теңдеудің кез келген шешімін қойғанда ол тұрақты санға айналады. Әдетте, интегралды осы қасиет бойынша да анықтайды: D облысында анықталған және дифференциалданатын, тұрақтыға өздігінен келтірілмейтін, ал (5) теңдеудің кез келген шешімінің бойымен алынғанда тұрақты санға тепе-тең функциясын (5) теңдеудің интегралы деп атайды.

Кейде дифференциалдық теңдеудің интегралының басқаша анықтамасы да қолданылады: функциясы берілген (5) теңдеудің интегралы деп аталады, егер оның осы теңдеу бойынша алынған толық дифференциалы нөлге тең болса, яғни

(19)

Бұл анықтамалар бір-біріне мағыналас түсініктер. Сондықтан оларды алмастырып қолдана беруге болады.