Методом наименьших квадратов

Для оценки вектора неизвестных параметров 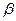применим метод наименьших квадратов. Так как произведение транспонированной матрицы 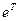на саму матрицу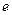

,

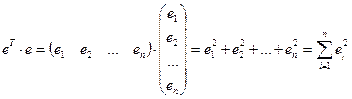то условие минимизации остаточной суммы квадратов запишется в виде:

.

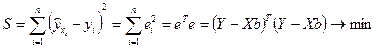Учитывая, что при транспонировании произведения матриц получается произведение транспонированных матриц, взятых в обратном порядке, т.е. 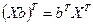, после раскрытия скобок получим:

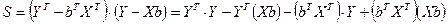
Произведение 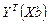есть матрица размерности 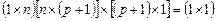, т.е. величина скалярная, следовательно, оно не меняется при транспонировании, т.е.

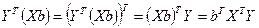
Поэтому условие минимизации примет вид:

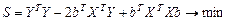
На основании необходимого условия экстремума функции нескольких переменных S 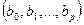, необходимо приравнять к нулю частные производные по этим переменным 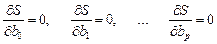или в матричной форме – вектор частных производных 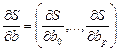должен быть ноль-вектором 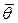, т.е. .

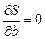Известно (из алгебры матриц) для векторов: , , .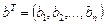

.

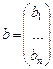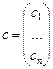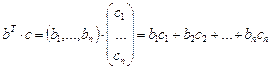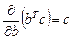
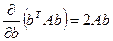, где 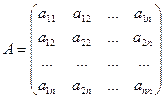– симметрическая матрица, в которой элементы, расположенные симметрично главной диагонали, равны.

Поэтому, полагая 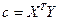, а матрица 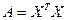(она является симметрической), найдем

,

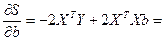
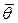откуда получаем систему нормальных уравнений в матричной форме для определения вектора :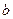

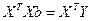. (3.4)

Найдем матрицы, входящие в это уравнение.

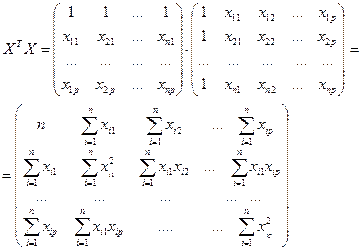
Матрица 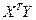есть вектор произведений n наблюдений объясняющих и зависимой переменных:

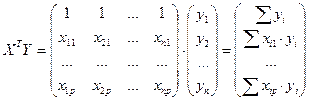
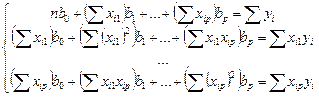(3.5)

При 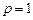получим систему нормальных уравнений:

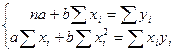
Для решения системы (3.5) или матричного уравнения (3.4) нужна еще одна предпосылка: 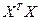- невырожденная матрица, т.е. 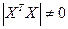. Тогда решение имеет вид:

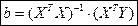. (3.6)

В модели (3.2) 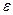- случайный вектор, Х – неслучайная матрица.