 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Основные положения регрессионного анализа
|
|
Теорема Гаусса – Маркова
В силу воздействия неучтенных случайных факторов и причин отдельные наблюдения переменной 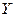 будут в большей или меньшей мере отклоняться от функции регрессии
будут в большей или меньшей мере отклоняться от функции регрессии 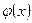 .
.
Рассмотрим линейный регрессионный анализ, для которого линейная парная регрессионная модель имеет вид:
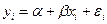 . (2.18)
. (2.18)
Отметим основные предпосылки регрессионного анализа.
1. В модели 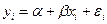 возмущение
возмущение 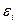 (или зависимая переменная
(или зависимая переменная  ) есть величина случайная, а объясняющая переменная
) есть величина случайная, а объясняющая переменная 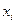 - величина неслучайная.
- величина неслучайная.
2. Математическое ожидание возмущения 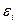 равно нулю:
равно нулю:
 (2.19)
(2.19)
(или математическое ожидание зависимой переменной  равно линейной функции регрессии:
равно линейной функции регрессии:  ).
).
3. Дисперсия возмущения 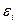 (или зависимой переменной
(или зависимой переменной  ) постоянна для любого
) постоянна для любого 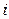
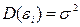 (2.20)
(2.20)
(или 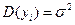 ) – условие гомоскедастичности или равноизменчивости возмущения (зависимой переменной)).
) – условие гомоскедастичности или равноизменчивости возмущения (зависимой переменной)).
4. Возмущения 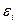 и
и 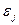 (или переменные
(или переменные 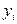 и
и 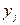 ) не коррелированы:
) не коррелированы:
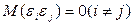 (2.21)
(2.21)
5. Возмущение 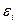 (или зависимая переменная
(или зависимая переменная  ) есть нормально распределенная случайная величина.
) есть нормально распределенная случайная величина.
В этом случае модель 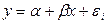 называется классической нормальной линейной регрессионной моделью.
называется классической нормальной линейной регрессионной моделью.
Для получения уравнения регрессии достаточно предпосылок 1 – 4. Требование выполнения предпосылки 5 (т.е. рассмотрение «нормальной регрессии») необходимо для оценки точности уравнения регрессии и его параметров.
Оценкой модели 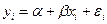 по выборке является уравнение регрессии
по выборке является уравнение регрессии  . Параметры этого уравнения
. Параметры этого уравнения 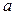 и
и 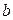 определяются на основе метода наименьших квадратов.
определяются на основе метода наименьших квадратов.
Воздействие неучтенных случайных факторов и ошибок наблюдений в модели 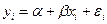 определяется с помощью дисперсии возмущений (ошибок) или остаточной дисперсии
определяется с помощью дисперсии возмущений (ошибок) или остаточной дисперсии  . Несмещенной оценкой этой дисперсии является выборочная остаточная дисперсия.
. Несмещенной оценкой этой дисперсии является выборочная остаточная дисперсия.
S 2 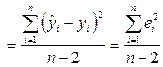 , (2.22)
, (2.22)
где 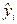 – групповая средняя, найденная по уравнению регрессии;
– групповая средняя, найденная по уравнению регрессии;  – выборочная оценка возмущения
– выборочная оценка возмущения 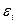 или остаток регрессии.
или остаток регрессии.
Возникает вопрос, являются ли оценки 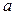 ,
, 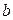 и
и 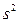 параметров
параметров 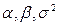 «наилучшими»? Ответ на этот вопрос дает следующая теорема.
«наилучшими»? Ответ на этот вопрос дает следующая теорема.
Теорема Гаусса – Маркова. Если регрессионная модель 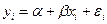 удовлетворяет предпосылкам 1 – 4, то оценки
удовлетворяет предпосылкам 1 – 4, то оценки 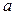 ,
, 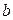 имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.
имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.
Таким образом, оценки 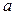 ,
, 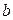 в определенном смысле являются наиболее эффективными линейными оценками параметров
в определенном смысле являются наиболее эффективными линейными оценками параметров 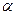 ,
, 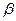 .
.
Дата публикования: 2014-11-18; Прочитано: 2066 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
