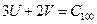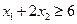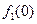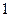|
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Модели развития хозяйственной организации 2 страница
|
|
Итальянский экономист Парето в первой половине ХХ века математически сформулировал один из самых распространенных критериев оптимальности для проверки следующего предположения: улучшает ли предложенное изменение в экономике общий уровень благосостояния?
Критерий Парето формулируется так: «Следует считать, что любое изменение, которое никому не причиняет убытков и которое некоторым приносит пользу, является улучшением».
Условие эффективности по Парето звучит так: Точка с координатами (U; V) из области D эффективна, если для любой точки 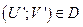 , такой, что
, такой, что 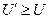 и
и 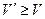 выполняется условие
выполняется условие 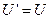 и
и 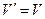 , т.е. точка
, т.е. точка 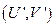 совпадает с точкой (U, V), следовательно, выбор исхода следует производить из множества эффективных точек.
совпадает с точкой (U, V), следовательно, выбор исхода следует производить из множества эффективных точек.
Отсюда следует и другое: принимаемое решение не может быть улучшено в интересах ни одного из партнеров, если оно ухудшает положение хотя бы одного из других.
Такое решение и отвечает оптимуму по Парето, потому, что в данных условиях лучшего получить не представляется возможным.
Однако какую именно эффективную точку следует признать оптимальной?
Сравним две эффективные точки 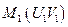 и
и  , представленные на рис. 5
, представленные на рис. 5
V
 M 2
M 2


 V2
V2

 V1 M1
V1 M1
 |
U2 U1 U
Рис. 5
Из рисунка видно, что 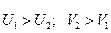 - для точки
- для точки 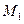 больше срок службы, а для
больше срок службы, а для  - скорость.
- скорость.
Для эффективных точек такая ситуация является типичной. Из определения ясно, что если для одной из точек области  оба показателя являются большими, чем для другой (или, по крайней мере, один показатель строго больше), то эта другая точка не будет эффективной.
оба показателя являются большими, чем для другой (или, по крайней мере, один показатель строго больше), то эта другая точка не будет эффективной.
Итак, считая для двух точек области D лучшей ту, для которой все показатели лучше, получаем, что для любых двух эффективных точек ни одна не является лучше другой.
Иначе говоря, эффективные точки являются несравнимыми между собой по предпочтению. Если мы все же хотим сравнивать эффективные точки, то для этого потребуется дополнительная информация. Чаще всего речь идет о том, чем именно может «пожертвовать» ЛПР ради того, чтобы получить единственное решение, а не множество эффективных точек. Точнее, нужно знать: сколькими единицами выигрыша по одному показателю можно компенсировать проигрыш единицы по другому показателю.
Аналогично строится множество эффективных решений и в случае, когда показателей не два, а больше (при их числе больше трех, геометрическая интерпретация теряет наглядность, но суть дела сохраняется).
Вывод: Одним из методов решения многокритериальных задач принятия решений является выбор оптимума по Парето (нахождение множества эффективных точек).
Для построения множества эффективных точек в каждой конкретной ЗПР используется так называемые «процедуры принятия решений». Они выполняются с применением численных методов и основаны на принципе отсечения ненужных исходов из всего множества возможных исходов.
Оставшееся в результате такого отсечения множества эффективных точек и есть решение ЗПР. Это множество называется кривая Эджворта. Каждая из множества этих точек не хуже другой, при этом выбрать какую-то одну из них в качестве решения можно только при наличии дополнительной информации, предоставленной ЛПР. Средствами математики выбрать единственное решение невозможно.
Что касается окончательного выбора решения, то он по-прежнему остается прерогативой человека. Только человек, с его непревзойденным умением решать неформальные задачи, принимать так называемые «компромиссные решения» (не строго оптимальные, но приемлемые по ряду критериев) может взять на себя ответственность за окончательный выбор.
Таким образом, для многокритериальных задач, как правило, не существует исхода наилучшего по всем показателям одновременно, поэтому для таких задач оптимальное решение называют компромиссным.
МЕТОДЫ НАХОЖДЕНИЯ КОМПРОМИССНОГО РЕШЕНИЯ
Поиск компромиссного решения осуществляется различными методами в зависимости от вида дополнительной информации.
Метод 1.
Каждому показателю, который оптимизируется, приписывается коэффициент важности или удельный вес. Например, в рассмотренной ранее задаче срок службы автомобиля (U) в 1,5 раза важнее для заказчика, чем его скорость (V) (в данном случае 1,5 означает отношение 3:2).
При таком подходе критерии «взвешиваются» по важности и им приписывается некий вес.
Записываем соотношение: 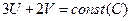 , где С – важность.
, где С – важность.
Выберем 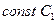 . Построим прямую
. Построим прямую 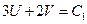 .
.
Будем двигать эту прямую вправо и вверх параллельно самой себе, пока не дойдем до северо-восточной части границы множества D. Точка пересечения этой прямой с границей множества D, и будет оптимальной (U *, V *).
 V
V 


 V*
V*
 |
|
D
 U*
U*
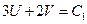 U
U
Рис. 6
Метод 2. «свертки критериев».
Пусть имеется набор критериев 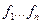 . С помощью дополнительной информации строится один собирательный критерий f (т.е. проводим процесс «свертки»), и далее решается задача для этого критерия.
. С помощью дополнительной информации строится один собирательный критерий f (т.е. проводим процесс «свертки»), и далее решается задача для этого критерия.
Фирме требуется выбрать оптимальную стратегию по обеспечению нового производства оборудованием. С помощью экспериментальных наблюдений были определены значения различных критериев функционирования соответствующего оборудования, которое выпускается тремя заводами-изготовителями. Соответствующие критерии приведены в таблице.
Таблица
| Варианты оборудования (Альтернативы или решения) | Частные критерии эффективности оборудования | |||
| Производитель-ность (Денежные единицы) | Стоимость оборудования (Денежные единицы) | Энергоем-кость (Условные единицы) | Надежность (Условные единицы) | |
| 1. Оборудование завода 1 (решение или альтернатива X 1) | 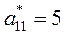
| 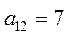
| 
| 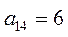
|
| 2. Оборудование завода 2 (X 2) | 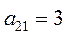
| 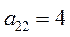
| 
| 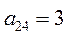
|
| 3. Оборудование завода 3 (Х 3) | 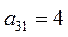
| 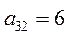
| 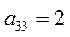
| 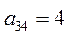
|
Примечание: * 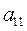 - критерий 1 для оборудования завода 1.
- критерий 1 для оборудования завода 1.
На основе экспертных оценок были определены веса каждого из критериев. Вес обозначим 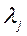 (еще его можно назвать уровень значимости или важность)
(еще его можно назвать уровень значимости или важность)
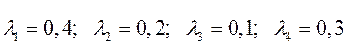
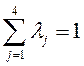
Так, например 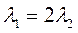 , следовательно, производительность для фирмы в 2 раза важнее.
, следовательно, производительность для фирмы в 2 раза важнее.
Если бы перед нами стояла задача выбора оборудования только по одному критерию, то проблемы бы не возникло. Например, если бы мы выбирали по производительности, то выбрали бы завод 1.
Но выбор оптимального решения по нескольким критериям является многокритериальной задачей.
На данном примере и рассмотрим метод «сверки критериев», который еще называют методом аддитивной оптимизации.
Найдем функцию
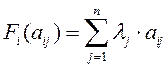 , где
, где 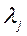 - важность критерия
- важность критерия
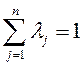
Для начала рассмотрим упрощенный вариант нашей задачи, а именно, будем считать, что в нашем распоряжении есть только два однородных критерия, т.е. критерии, имеющие одинаковую размерность. Выберем производительность и стоимость.
Теперь будем решать двухкритериальную задачу.
Пусть 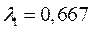 и
и 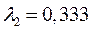 .
.
Рассчитаем значения 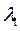 и
и 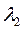 из системы уравнений
из системы уравнений
|
|
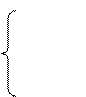
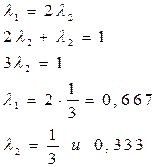
Найдем значения аддитивных функций для упрощенного примера.
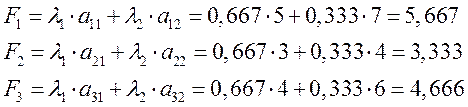
Из полученных значений аддитивных функций, выбираем максимальное 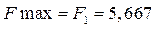 , следовательно, первый вариант оборудования является предпочтительным по двум первым критериям.
, следовательно, первый вариант оборудования является предпочтительным по двум первым критериям.
Эту же задачу можно решать по энергоемкости и надежности.
Пусть 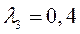 и
и 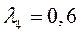
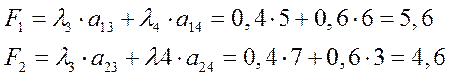
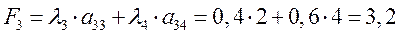
Вывод: по энергоемкости и надежности также предпочтительным является оборудование завода 1.
Если же все критерии имеют разную размерность. То пред решением необходимо провести процедуру нормализации критериев, т.е. привести критерии к безразмерному виду.
Нормализация – процесс пересчета критериев.
Для этого определим max и min по каждому критерию (максимальное и минимальное в каждом столбце):

Затем по экономическому смыслу выделим группу критериев, которые максимизируются, и пронумеруем их 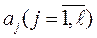 , и группу критериев которые минимизируются
, и группу критериев которые минимизируются 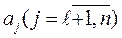 .
.
Критерии производительность и надежность попадут в первую группу, а во вторую стоимость и энергоемкость.
Значения нормализованных критериев определяются из следующих соотношений:
 , для
, для 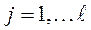 (для критериев, которые максимизируются)
(для критериев, которые максимизируются)
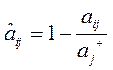 , для
, для 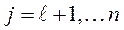 (для критериев, которые
(для критериев, которые
минимизируются)
Оптимальным будет тот вариант, который обеспечит максимальное значение аддитивной функции
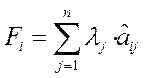
1. Найдем 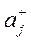
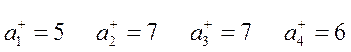
2. Найдем 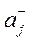
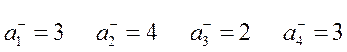
3. Максимизируются два критерия: производительность 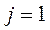 и надежность
и надежность 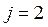 , следовательно,
, следовательно, 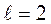 .
.
Тогда критерии, которые минимализируются имеют номера 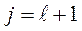 , и это – стоимость
, и это – стоимость 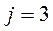 и надежность
и надежность 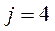 .
.
Находим нормализованные критерии:
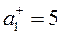
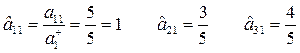
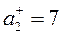
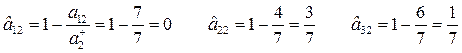
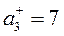
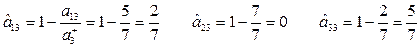
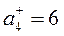
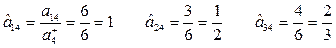
Затем найдем аддитивные функции
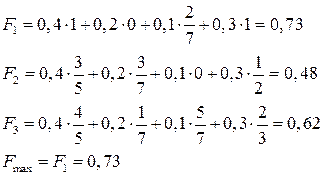
Вывод: необходимо приобрести оборудование завода 1.
Метод 3. метод уступок решения задач многокритериальной оптимизации
Пусть в задаче многокритериальной оптимизации есть несколько критериев
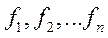
В таких задачах критерий – это синоним целевой функции.
Расположим их по значимости, причем самый важный будет иметь номер 1 и т.д.
I этап: Решаем задачу по первому критерию на области допустимых решений (ОДР) D, при этом получим оптимальное значение первого критерия f 1.
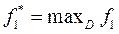
II этап: Делаем «уступку» по первому критерию, т.е. уменьшаем величину 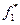 до значения
до значения 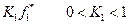 , где К 1 – уступка по первому критерию.
, где К 1 – уступка по первому критерию.
III этап: Вводим в задачу дополнительное ограничение
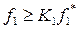 (*)
(*)
IV этап: Решаем задачу по второму критерию с новой системой ограничений, а именно, к ОДР добавляется еще одно условие:
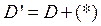 , т.е.
, т.е. 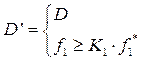
скорее всего, ОДР сузится, и т.д. последовательно по всем критериям.
В результате решения по второму критерию получим

Будем действовать так последовательно по всем критериям.
Процесс заканчивается, когда будет получено решение по всем критериям. Окончательный план и будет эффективным. При этом получим экстремальное значение критерия наименьшей важности (fm) при условии гарантированных значений предшествующих критериев.
Пример 1. Решение с помощью графического метода.
Рассмотрим задачу о выпуске продуктов двух видов, при условии максимизации прибыли и минимизации затрат на хранение в условиях ограниченности ресурсов
 (прибыль)
(прибыль)
 (затраты на хранение)
(затраты на хранение)
Область допустимых значений
D 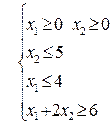 ,
,
где x 1 и x 2 - количество выпускаемой продукции первого и второго вида.
Уступка по первому критерию 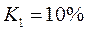 , что означает, что можно уменьшить
, что означает, что можно уменьшить 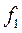 на 10%, т.е. оставить 90% или 0,9.
на 10%, т.е. оставить 90% или 0,9.
Самым важным критерием будет прибыль, следовательно, начинаем решать задачу по первому критерию на область D.

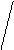
|

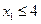
 | |||
| |||
|


|
|
|
|
|


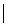
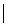
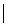
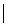
Рис. 7
1) Построим прямую
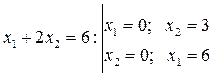
2) И еще две прямые 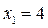 и
и 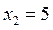
3) Затем определяем положение ОДР. Например, для прямой 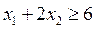 , подставляем точку с координатами
, подставляем точку с координатами 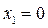 и
и  в формулу неравенства, и получаем
в формулу неравенства, и получаем 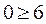 . Это неравенство неверно, следовательно, ОДР будет направлена от точки (0;0), ставим стрелку в сторону от нуля.
. Это неравенство неверно, следовательно, ОДР будет направлена от точки (0;0), ставим стрелку в сторону от нуля.
4) Определяем координаты конца вектора нормали из критерия 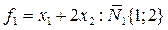 , и строим этот вектор.
, и строим этот вектор.
5) Перпендикулярно вектору нормали строим линию уровня 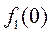 . Двигаем линию уровня параллельно самой себе в направлении вектора нормали
. Двигаем линию уровня параллельно самой себе в направлении вектора нормали  , до тех пор пока линия уровня не станет опорной к ОДР (т.е. не будет касаться ее в одной точке) и находим
, до тех пор пока линия уровня не станет опорной к ОДР (т.е. не будет касаться ее в одной точке) и находим 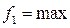 в точке А с координатами
в точке А с координатами 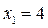 и
и 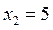 . Отсюда
. Отсюда 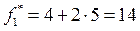 .
.
6) Выводим уступку на 10%.
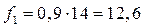 .
.
Теперь решаем задачу с добавлением ограничения в области 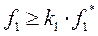 , т.е.
, т.е. 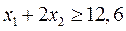 и получаем область
и получаем область 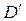
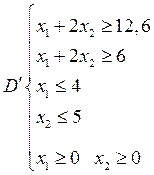
Задачу решаем по векторному критерию
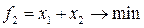
7) Строим область 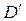 . Добавляем прямую:
. Добавляем прямую:
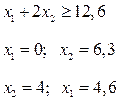
Определяем конец вектора нормали 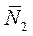 из второго критерия
из второго критерия
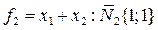
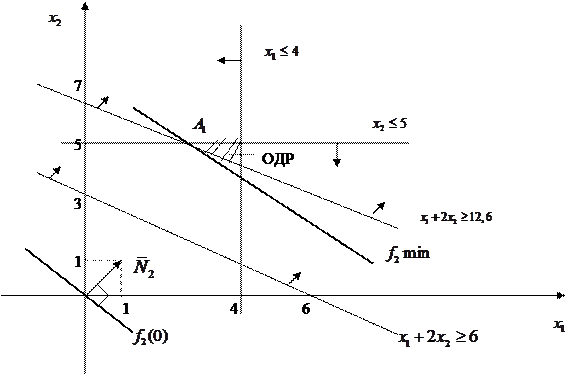 |
Рис. 8
Строим линию уровня 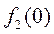 перпендикулярно вектору
перпендикулярно вектору 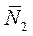 и находим точку А1, которая является точкой пересечения прямых
и находим точку А1, которая является точкой пересечения прямых 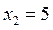 и
и 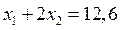 .
.
Отсюда получаем 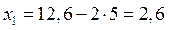 .
.
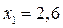 и
и 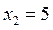 .
.
Тогда 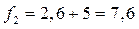
Ответ:
Компромиссным планом будет выпуск 2,6 ед. одного продукта, 5 ед. второго продукта, при этом max прибыли = 12,6, а min затрат = 7,6. Субоптимальные планы (т.е. оптимальные планы на каждом этапе), приводящие к компромиссному решению образуют цепочку (точка А  точка А 1 и т.д.).
точка А 1 и т.д.).
Пример 2. Решение с помощью симплексного метода.
Найдем компромиссное решение следующей задачи:
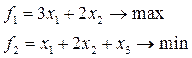
при ограничениях
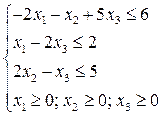
При условии, что уступка по первому критерию составляет 50 %.
Уступка 50 % означает, что можно отклониться от максимального значения первой целевой функции ровно на половину.
Решение:
1. Решаем задачу по первому критерию, т.е. решаем следующую задачу линейного программирования с помощью симплексного метода:
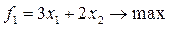
при ограничениях
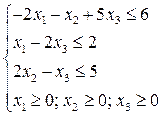
1.1. Приводим задачу к каноническому виду, для этого вводим дополнительные переменные 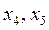 и
и 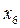 .
.
Дата публикования: 2014-11-02; Прочитано: 255 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!