 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Временные ряды и их структура
|
|
Большинство эконометрических моделей строится как динамические эконометрические модели. Это означает, что моделирование причинно-следственных связей между переменными осуществляется во времени, а исходные данные представлены в форме временных рядов.
Временной ряд х t (t=1; n) – ряд значений какого-либо показателя за несколько последовательных промежутков времени.
Каждый временной ряд хt складывается из следующих основных составляющих (компонентов):
1. Тенденции, характеризующей общее направление динамики изучаемого явления. Аналитически тенденция выражается некоторой функцией времени, называемой трендом (Т).
2. Циклической или периодической составляющей, характеризующей циклические или периодические колебания изучаемого явления. Колебания представляют собой отклонения фактических уровней ряда от тренда. Объем продаж некоторых товаров подвержен сезонным колебаниям. Сезонные колебания (S) – периодические колебания, которые имеют определенный и постоянный период равный годовому промежутку. Конъюнктурные колебания (К) связаны с большими экономическими циклами, период таких колебаний – несколько лет.
3. Случайной составляющей, которая является результатом воздействия множества случайных факторов (Е).
Тогда уровень ряда можно представить как функцию от этих составляющих (компонентов): 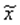 =f(T, K, S, E).
=f(T, K, S, E).
В зависимости от взаимосвязи между составляющими может быть построена либо аддитивная модель: 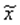 =T+K+S+E, либо мультипликативная модель:
=T+K+S+E, либо мультипликативная модель: 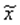 =T·K·S·E ряда динамики.
=T·K·S·E ряда динамики.
Для определения состава компонентов (структуры временного ряда) в модели временного ряда строят автокорреляционную функцию.
Автокорреляция– корреляционная связь между последовательными уровнями одного и того же ряда динамики (сдвинутыми на определенный промежуток времени L - лаг). То есть, автокорреляция - это связь между рядом: x1, x2,... xn-l и рядом x1+l, x2+l,...,xn, где L - положительное целое число. Автокорреляция может быть измерена коэффициентом автокорреляции:
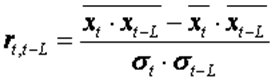 ,
где
,
где 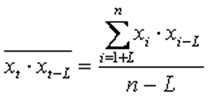 ,
,
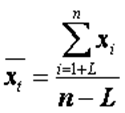 – средний уровень ряда (x1+L, x2+L,...,xn),
– средний уровень ряда (x1+L, x2+L,...,xn),
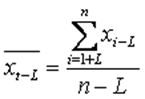 средний уровень ряда (x1, x2,..., xn-L),
s t, s t-L – средние квадратические отклонения, для рядов (x1+L, x2+L,..., xn) и (x1, x2,..., xn-L) соответственно.
средний уровень ряда (x1, x2,..., xn-L),
s t, s t-L – средние квадратические отклонения, для рядов (x1+L, x2+L,..., xn) и (x1, x2,..., xn-L) соответственно.
Лаг (сдвиг во времени) определяет порядок коэффициента автокорреляции. Если L =1, то имеем коэффициент автокорреляции 1-ого порядка rt,t-1, если L =2, то коэффициент автокорреляции 2-ого порядка rt,t- 2 и т.д. Следует учитывать, что с увеличением лага на единицу, число пар значений, по которым рассчитывается коэффициент автокорреляции уменьшается на 1. Поэтому обычно рекомендуют максимальный порядок коэффициента автокорреляции равный n /4.
Рассчитав несколько коэффициентов автокорреляции, можно определить лаг (L), при котором автокорреляция (rt,t-L) наиболее высокая, выявив тем самым структуру временного ряда.
1. Если наиболее высоким оказывается значение коэффициента автокорреляции первого порядка rt,t- 1, то исследуемый ряд содержит только тенденцию.
2. Если наиболее высоким оказался коэффициент автокорреляции rt,t-L порядка L, то ряд содержит колебания периодом L.
3. Если ни один из rt,t-L не является значимым, можно сделать одно из двух предположений:
◦ либо ряд не содержит тенденции и циклических колебаний, а его уровень определяется только случайной компонентой;
◦ либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.
Последовательность коэффициентов автокорреляции 1, 2 и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости значений коэффициентов автокорреляции от величины лага (порядка коэффициента автокорреляции) называют коррелограммой.
Дата публикования: 2015-11-01; Прочитано: 1193 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
