Анализ влияния дохода и цен на спрос

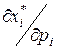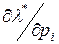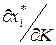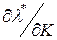Как мы видели в предыдущих параграфах, для оценки различных ситуаций в сфере потребления применяются предельный спрос и предельная полезность денег по ценам ( и ) и доходу ( и ). Поэтому желательно иметь формулы для их вычисления. Если общее решение задачи (3.4.1) - (3.4.2) для конкретной функции полезности u найдено в виде функций

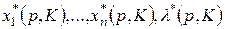(3.6.1)

от 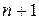параметра 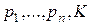, то требуемые предельные величины можно найти, вычисляя частные производные функций (3.6.1) по 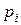и К. Но эти же предельные величины можно найти не решая задачу (3.4.1) - (3.4.2), а сразу из системы необходимых и достаточных условий оптимальности (3.4.5) - (3.4.8).

Зная теперь, что оптимальное решение 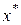задачи (3.4.1) - (3.4.2) лежит на бюджетной линии (см. рис. 3.7), мы можем априори считать, что доход К будет использован полностью. Тогда в (3.4.2) будет строгое равенство, и система (3.4.5) - (3.4.8) примет вид:

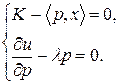(3.6.2)

Так как эта система зависит от параметров р, К и содержит неизвестные 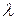, x, то нам удобно ввести обозначения:

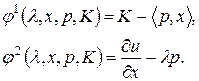(3.6.3)

Как и ранее, будем предполагать, что функция u дважды непрерывно дифференцируема и удовлетворяет условиям (1) - (2).

Система (3.6.2) будет разрешимой относительно 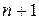переменных 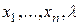, если определитель матрицы Якоби (матрица первых производных системы (3.6.2))

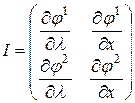
отличен от нуля. Покажем, что это так и есть. С учетом обозначений (3.6.3) получаем:

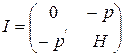
где 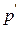- транспонированный вектор 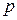, H - матрица Гессе (матрица вторых производных системы (3.6.2)). В координатной форме

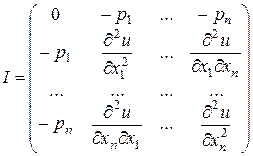
- есть "окаймляющая" ценами товаров матрица Гессе. По условию (2) матрица Гессе отрицательно определена и поэтому невырожденна. Следовательно, определитель матрицы Якоби не равен нулю, и система (3.6.2) имеет решение (по 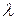и x).

Перейдем к вычислению требуемых предельных величин.

1. Вычисление предельных величин 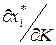и 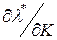(влияние дохода на 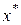и .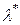

Подставим (3.6.1) в систему (3.6.2):

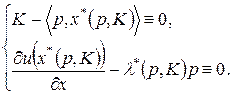(3.6.4)

и продифференцируем ее по K:

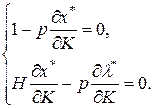
Перепишем эту систему в форме, удобной для перехода к матричной записи:

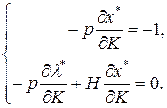
В матричной форме эта система имеет вид:

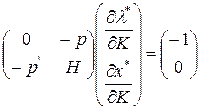(3.6.5)

где

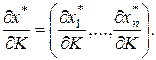
Решая систему (3.6.5), можно найти искомые предельные величины по доходу.

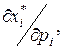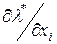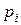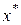2. Вычисление предельных величин и (влияние цены на и 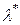при условии постоянства остальных цен 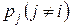и дохода К).

Дифференцируя систему (3.6.4) по 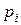, получаем (в координатной форме):

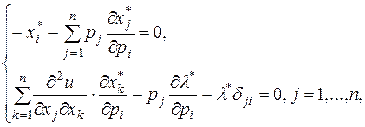(3.6.6)

где

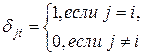
- символ Кронекера. Запишем систему (3.6.6) сначала в векторной, затем в матричной форме:

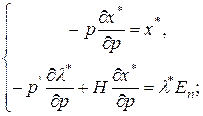
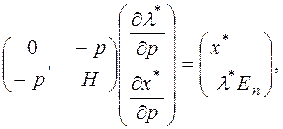(3.6.7)

где

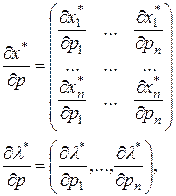
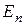- единичная 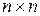-матрица ( 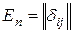- матрица с нулевыми элементами за исключением диагональных, равных 1).

Решая систему (3.6.7), можно найти искомые предельные величины по цене i -го товара.

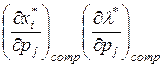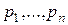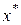3. Вычисление предельных величин (влияние цен на и 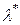при условии компенсации дохода так, чтобы полезность была неизменной).

Используя систему (3.6.2), найдем полные дифференциалы функций u и К:

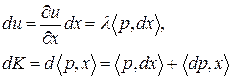
Для того, чтобы полезность оставалась неизменной, т.е. чтобы 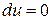, необходимо, чтобы 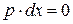(так как 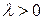), а это справедливо, если 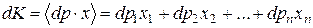. Содержательно это означает, что при возрастании, например, цены 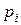до 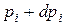приращение дохода, обеспечивающее неизменность полезности, равно .

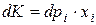Дифференцируя (3.6.4) по 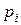, когда 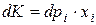, получаем:

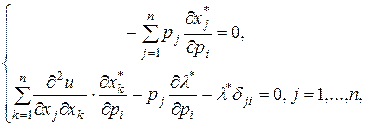
Поясним, что первое уравнение этой системы получается из (3.6.6) при условии

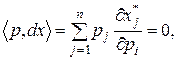
так как в этом случае из (3.6.6) следует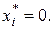

В векторной форме эта система имеет вид:

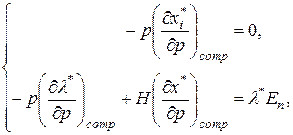
где 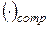- означает компенсированное изменение цен.

Запишем теперь в матричную форму:

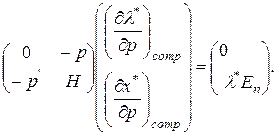(3.6.8)

Решая систему (3.6.8), можно найти искомые предельные величины при компенсированном изменении цен.

Все три матричных (3.6.5), (3.6.7) и (3.6.8) могут быть объединены в одно матричное уравнение:

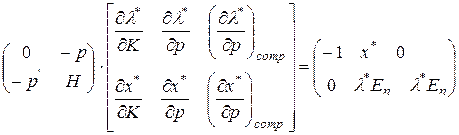(3.6.9)

Это уравнение называется основным матричным уравнением теории потребления. Матрица

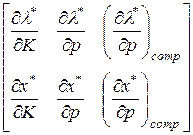
называется матрицей сравнительной статики, а ее элементы - показателями сравнительной статики. Такое название объясняется тем, что эти показатели характеризуют чувствительность 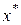и 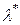к изменениям параметров р и К путем сравнения положения оптимума в статике до и после того, как эти параметры изменились.

Поскольку левая часть уравнения (3.6.9) есть невырожденная матрица (ибо такой является Якобиан), то оно может быть разрешено относительно показателей сравнительной статики. Решение уравнения (3.6.9) связано с понятием уравнения Слуцкого, чему и будет посвящен следующий параграф.