Оптимизационная модель задачи потребительского выбора

В этом параграфе мы приведем и исследуем классическую математическую модель задачи индивидуального потребительского выбора. Содержательно эту задачу можно сформулировать так: потребителю нужно приобрести (купить) на рынке необходимые ему виды товаров в таком количестве, чтобы их потребление доставило максимальное удовлетворение (пользу); при этом суммарная стоимость купленных товаров не должна превышать его дохода (бюджета).

Последнее условие называется бюджетным ограничением и оно подчеркивает всегда ограниченные покупательские возможности потребителя.

Обращает на себя внимание "скудность" постановки задачи. Так, например, не говорится о минимальном прожиточном уровне, ниже которого объем потребления не может опускаться; нет ограничения на доход потребителя и т.д. Однако, следует исходить из того, что эта постановка общая и в случае необходимости более подробного моделирования все недостающие сведения можно "прочитать между строчками" этой постановки. Мы же будем принимать эту постановку как исходную, ее и будем моделировать.

В начале § 1 мы перечислили те важнейшие факторы, которые будучи формализованы и связаны подходящими математическими соотношениями и дают требуемую модель. Это товар и его цена, цель и бюджет потребителя, его покупательская способность.

Приведем сначала необходимые обозначения, хотя некоторые из них уже были введены в §§3.1, 3.2. Пусть - набор товаров, где x_i - количества товара вида i, n - число видов товаров, 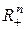- пространство товаров; 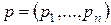- вектор цен товаров, где p_i - цена единицы товара вида i; K - доход (бюджет) потребителя.

Мы рассматриваем статическую задачу, поэтому эти величины не зависят от фактора времени. Параметры p_i и K считаются постоянными величинами, причем цены считаются рыночными, а доход не структуризуется, то есть нас не интересует из каких частей он складывается. Компоненты x_i вектора являются неизвестными переменными. Модель составляется как раз для определения "оптимальных" значений этих переменных для данного потребителя. Цель потребителя будем описывать с помощью функции полезности 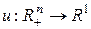(см. § 3.2 и определение 3.1), относительно которой будем предполагать выполнение условий (1) и (2). Наконец, мы рассматриваем некоторого "обобщенного" потребителя, никак не характеризуя его индивидуальные особенности, за исключением априорного предложения о существовании функции полезности, отражающей его индивидуальные предпочтения в 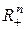(см. Теорему 3.1).

С учетом всего сказанного выше, модель задачи потребительского выбора имеет вид:

(3.4.1)

при ограничениях

(3.4.2)

Обозначим через 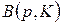множество всевозможных товаров, допустимых потребителю при ценах p и доходе K:

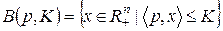(3.4.3)

называемое бюджетным множеством. Графическое изображение этого множества показано на рис.3.6.

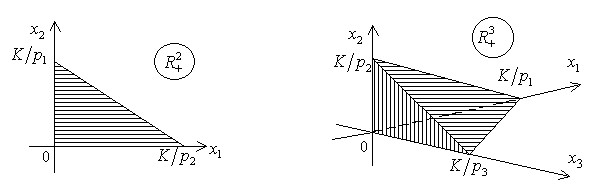
Рис. 3.6. Графическое изображение бюджетного множества

Граница

множества 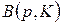называется бюджетной линией.

Оптимальным решением задачи (3.4.1)-(3.4.2) называется такой вектор 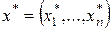, что

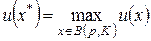(3.4.4)

Определение 3.3. Оптимальное решение 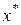задачи (3.4.1) - (3.4.2) называется спросом потребителя.

Данное формальное определение спроса отражает классическое понятие спроса как платежеспособную потребность.

Всегда ли существует оптимальное решение задачи (3.4.1) - (3.4.2)?

Поскольку мы имеем дело с оптимизационной задачей (линейный или нет в зависимости от функции полезности u), то на этот вопрос следует ответить с точки зрения теоремы Вейерштрасса. Так как функция полезности непрерывна по факту ее существования (см. Теорему 3.1), основная сложность заключается в компактности множества (3.4.3), на котором ищется максимум функции u (см. (3.4.4)). В метрическом пространстве 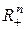, как известно, компактность множества равнозначно его замкнутости и ограниченности. Так как бюджетное множество замкнуто по определению, то остается изучить его ограниченность.

Покажем, что ограниченность не всегда имеет место. Предположим, для некоторого i p_i=0. Как следует из (3.4.2), в этом случае "допустимым" становится любой вектор 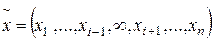, то есть 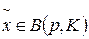, что говорит о неограниченности бюджетного множества. А это, в свою очередь, может привести к отсутствию оптимального решения задачи (3.4.1)-(3.4.2) (напр., в случае неограниченности функции u, что является следствием ненасыщаемости потребителя (см. свойство a^'₅ в §3.2)). Однако, если потребитель ненасыщаем по всем товарам, то множество 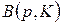оказывается ограниченным. Более строже этот факт сформулирован в следующем утверждении.

Теорема 3.3. Пусть бюджетное множество (3.4.3) обладает следующим свойством: если в последовательност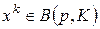и при 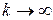имеет место 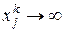для некоторого j, то 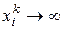для всех i=1,...,n. Тогда бюджетное множество ограничено и в задаче (3.4.1)-(3.4.2) существует оптимальное решение. Если при этом функция u строго вогнута на множестве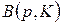 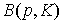, то оптимальное решение единственно.

Итак, при фиксированных ценах 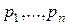и заданном доходе K оптимальное потребление определяется компонентами 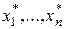решения 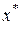задачи (3.4.1)-(3.4.2).

Выяснив существование оптимального решения задачи потребителя, займемся вопросом его вычисления. Для этого воспользуемся методом множителей Лагранжа.

Составим функцию Лагранжа для нашей задачи:

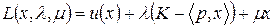
где 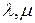-множители Лагранжа. Выпишем необходимые условия оптимальности (условия Куна-Таккера),которые благодаря условиям (2) будут и достаточными:

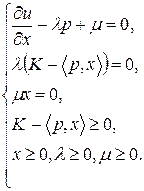
Не умаляя общности рассуждений, примем следующее предложение: потребитель приобретает все виды товаров, то есть 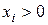для всех i=1,...,n (в противном случае можно уменьшить размерность пространства 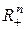) и будем считать, что 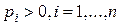. Тогда из третьего равенства следует 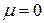и необходимые и достаточные условия принимают вид:

Эта система разрешима относительно n+1 неизвестных 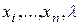, так как имеется n+1 уравнение (3.4.5) и (3.4.6). Все переменные и частные производные здесь вычисляются в точке 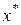. Значение 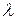соответствующее (в силу уравнений (3.4.5) и (3.4.6)) точке 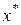обозначим .

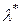Для пары 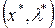из (3.4.5) получаем:

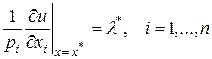(3.4.9)

Отсюда следует важный вывод о том, что в условиях оптимального потребления (то есть в условиях набора 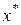) отношение предельной полезности к цене одинаково для всех товаров. Исходя из (3.4.9) оптимальный множитель Лагранжа 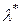интерпретируется как предельная полезность одной единицы цены или просто предельная полезность денег.

Поэтому равенство

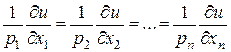
означает, что предельная полезность одной единицы денег одинаково для каждого товара и именно при таком распределении бюджета потребитель получает максимум полезности. Для объяснения этого факта обратимся к рис. 3.3. Если полезность от расходования дополнительного доллара на продукт питания выше, чем от доллара на одежду, то потребитель может увеличить полезность за счет роста расходов на питание. Таким образом, увеличение расходов на питание вызовет уменьшение расходов на одежду и это будет продолжаться до тех пор, пока предельная полезность на питание будет выше чем на одежду. По закону Госсена предельная полезность продуктов питания постепенно снизится, вызывая рост расходов на одежду. Только тогда, когда предельная полезность дополнительного доллара расходов становится одинаковой для питания и одежды, будет достигнут максимум полезности.

Из равенства (3.4.9) следует так же вывод о том, что цены должны определяться исходя из предельной полезности товаров и денег:

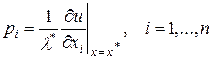
Так как 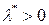(следует из (3.4.5)), то из (3.4.6) получаем

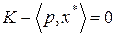
Последнее означает, что точка максимума 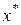задачи (3.4.1) - (3.4.2) лежит на бюджетной линии. В случае двух товаров имеем (см. рис 3.7):

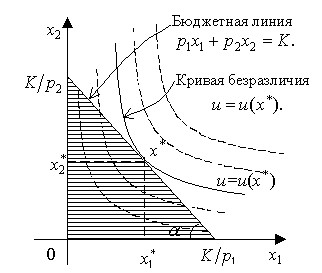
Рис. 3.7. Решение задачи потребителя

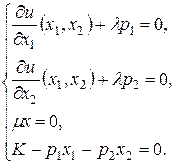
Наклон бюджетной линии равен

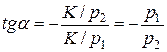
Наклон кривой безразличия находится из выражения 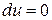, то есть

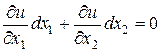
и составляет

Так как в точке касания 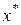наклон кривой безразличия равен наклону бюджетной линии, то

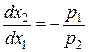
или

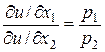(3.4.10)

Как видно из (3.4.9), и в частности, из (3.4.10),

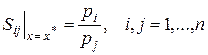
то есть в оптимальном наборе товаров 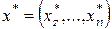предельная норма замещения товара i товаром j оценивается отношением их цен (то есть зависит исключительно от их цен).

Как показывает рис. 3.7, оптимальное решение задачи (3.4.1)-(3.4.2) геометрически является точкой касания кривой безразличия и бюджетной линии. Для строго вогнутой функции полезности такая точка касания единственна (см. Теорему 3.3).

С помощью рис. 3.7 можно анализировать различные последствия, связанные с изменением цен и дохода.

Рис. 3.8. Эффекты замещения и дохода

Будем считать, что все товары нормальные (качественные), то есть при увеличении дохода потребление увеличивается. Нас интересуют следующие вопросы:

а) изменение покупательской способности: как изменится спрос на товары при изменении их цен и неизменном доходе?

в) эффект замещения: как изменится потребление товаров, когда при изменении цен полезность должна оставаться на прежнем уровне?

г) эффект дохода: как изменится потребление товаров при изменении дохода потребителя и неизменных ценах?

Обсудим случай а). Предположим, что снижается цена первого товара. Тогда бюджетная линия из положения АВ переходит в положение АС (рис.3.8). Так как кривые безразличия заполняют все пространство , то обязательно найдется одна кривая безразличия, имеющая с бюджетной линией АС точку касания. Обозначим эту точку 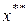. Она и будет оптимальным решением задачи потребителя при новых ценах. В точке 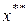полезность будет больше чем в точке 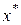, за счет увеличения на величину 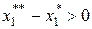потребления первого товара. Это стало возможным в результате роста покупательской способности потребителя (его реального дохода), благодаря снижению цены на первый товар. Что произошло при этом с объемом потребления второго товара? Он снизился на величину 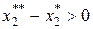. Здесь отражена та реальность, когда люди потребляют большее количество (качественного) товара, который подешевел, и меньшее количество тех товаров, которые остались на прежнем ценовом уровне или подорожали.

Читателю предлагается самостоятельно анализировать случаи уменьшения цены товара и одновременного изменения цен на оба вида товара.

Рассмотрим эффект замещения (случай в)). Предположим опять, что первый продукт стал более дешевым (по сравнению с тем, что было в точке 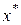). Так как при этом полезность не должна меняться, то эффект замещения отражается смещением точки 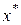вдоль кривой безразличия 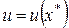, то есть новое оптимальное решение 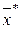задачи потребителя будет находится на одной кривой безразличия с точкой 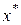(рис. 3.8). Бюджетная линия A'C', касающаяся кривой безразличия 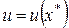в точке 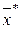, параллельна изменившейся бюджетной линии АС и удалена от нее на величину изменения реального дохода (покупательской способности). Следовательно, эффект замещения представляется величиной .

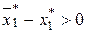Проверив эффект дохода (случай г)) самостоятельно убедитесь, что он характеризуется ростом потребления первого товара на величину .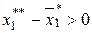

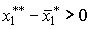Мы видим, что пользуясь решением задачи (3.4.1) - (3.4.2) можно анализировать различные ситуации и ответить на многие вопросы, круг и глубина которых зависит от творческих способностей исследователя.

В зависимости от условий конкретной задачи, свойств товаров и прочего в выражении (3.4.1) можно либо использовать одну из известных функций полезности, например, одну из функций (3), (4), (3.2.8) - (3.2.12), либо построить новую функцию полезности.

Надо заметить, что в теории потребления нет общих или универсальных методов построения функций полезности. Известныо лишь частные методы для некоторых отдельных классов таких функций. Приведем один способ приближенного построения так называемых аддитивных функций полезности. Такие функции применяются в тех случаях, когда полезность набора товаров 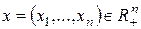складывается как сумма полезностей товаров отдельных видов:

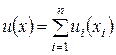(3.4.11)

Примером аддитивной функции полезности является функция (3); напротив, функция (4) и (3.2.8) неаддитивны.

Будем считать, что функция (3.4.11) задана на n-мерном параллелепипеде:

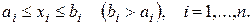
Обозначим 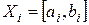. Тогда пространство товаров имеет вид:

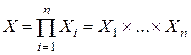
(это и есть n-мерный параллелепипед).

Идеи метода заключаются в построении линий безразличия на каждом из n-1 граней параллелепипеда X. Исходной информацией для этого является определяемость линий безразличия условиями замещения товаров (см. рис. 3.3).

Рис. 3.9. Точки разбиения отрезков в 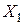и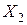

Алгоритм метода следующий.

1. Выявление взаимозаменяемых товаров: в общем случае товары вида i₀ и j₀ будут взаимозаменяемыми, если существует последовательность взаимозаменяемых пар

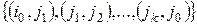(3.4.12)

2. Вычисление предельных норм замещения: для каждой пары (i,j) из (3.4.12) вычисляют величину S_ij по формуле (3.3.9) или (3.3.5).

3. Построение кривых безразличия на гранях параллелепипеда Х: с помощью чисел S_ij, полученных в п.2, сроят по одной линии безразличия в прямоугольниках 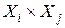(см. рис. 3.3).

4. Разбиение граней одного из прямоугольников 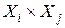точками: выбирают один из прямоугольников, например, 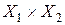и для кривой безразличия строят ее близкое смещение (то есть новую кривую безразличия) (см. рис. 3.9); разбиение отрезков Х₁ и Х₂ получают с помощью "лестницы" между двумя кривыми безразличия.

5. Построение функции полезности для товара i=1: для полученного в п.4 разбиения отрезка Х₁ строят функцию полезности u₁(x₁) предполагая, что на каждом интервале разбиения функция u₁ возрастает на одну единицу (рис. 3.10).

Рис. 3.10. График функции Рис. 3.11. Разбиение отрезка Х₃

полезности u₁

6. Последовательное разбиение остальных отрезков X_i: эту процедуру проводят индуктивно, как показано на рис. 3.11.

7. Последовательное построение функции полезности для остальных товаров: для получения в п.6. последовательных разбиений отрезков X_i строят функции полезности u_i(x_i) как в п.5.

8. Построение общей функции полезности: после того, как получены все u_i, i=1,...,n, полагают .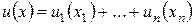

Заметим, что точность аппроксимации функции полезности u зависит от близости исходной и смещенной кривых безразличия в п.4.

Теоретическое обоснование приведенного алгоритма можно найти в [Математический аппарат экономического моделирования (Под. ред. Гольштейна Е. Г.). – М.: Наука, 1983].