 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Спецификация модели. Ошибки спецификации
|
|
Журнал «Quarterly Review of Economics and Business» приводит данные о вариации дохода кредитных организаций США за период 25 лет в зависимости от изменений годовой ставки по сберегательным депозитам и числа кредитных учреждений. Логично предположить, что, при прочих равных условиях, предельный доход будет положительно связан с процентной ставкой по депозиту и отрицательно с числом кредитных учреждений. Построим модель следующего вида:
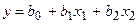 ,
,
где
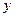 – прибыль кредитных организаций (в процентах);
– прибыль кредитных организаций (в процентах);
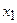 – чистый доход на один доллар депозита;
– чистый доход на один доллар депозита;
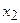 – число кредитных учреждений.
– число кредитных учреждений.
Исходные данные для модели:
| Годы | 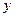
| 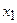
| 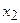
| |
| 3,92 | 0,75 | |||
| 3,61 | 0,71 | |||
| 3,32 | 0,66 | |||
| 3,07 | 0,61 | |||
| 3,06 | 0,70 | |||
| 3,11 | 0,72 | |||
| 3,21 | 0,77 | |||
| 3,26 | 0,74 | |||
| 3,42 | 0,90 | |||
| 3,42 | 0,82 | |||
| 3,45 | 0,75 | |||
| 3,58 | 0,77 | |||
| 3,66 | 0,78 | |||
| 3,78 | 0,84 | |||
| 3,82 | 0,79 | |||
| 3,97 | 0,70 | |||
| 4,07 | 0,68 | |||
| 4,25 | 0,72 | |||
| 4,41 | 0,55 | |||
| 4,49 | 0,63 | |||
| 4,70 | 0,56 | |||
| 4,58 | 0,41 | |||
| 4,69 | 0,51 | |||
| 4,71 | 0,47 | |||
| 4,78 | 0,32 |
Анализ данных начинаем с расчета дескриптивных статистик:
Таблица 3.1. Дескриптивные статистики
| y | x1 | x2 | |
| Объём выборки | |||
| Средняя арифметическая | 0,67 | 3,85 | 7243,32 |
| Среднее квадратическое (стандартное) отклонение | 0,14 | 0,58 | 1003,21 |
| Коэффициент вариации | 20,61 | 15,02 | 13,85 |
| Асимметрия | -0,92 | 0,28 | 0,94 |
| Эксцесс | 0,58 | -1,31 | -1,28 |
Сравнивая значения средних величин и стандартных отклонений, находим коэффициент вариации, значения которого свидетельствуют о том, что уровень варьирования признаков находится в допустимых пределах (< 0,35). Значения коэффициентов асимметрии и эксцесса указывают на отсутствие значимой скошенности и остро-(плоско-) вершинности фактического распределения признаков по сравнению с их нормальным распределением. По результатам анализа дескриптивных статистик можно сделать вывод, что совокупность признаков – однородна и для её изучения можно использовать метод наименьших квадратов (МНК) и вероятностные методы оценки статистических гипотез.
Перед построением модели множественной регрессии рассчитаем значения линейных коэффициентов парной корреляции. Они представлены в матрице парных коэффициентов (таблица 3.2) и определяют тесноту парных зависимостей анализируемыми между переменными.
Таблица 3.2. Коэффициенты парной линейной корреляции Пирсона
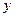
| 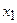
| 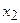
| |
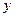
| 1,0000 (0,0) | -0,7039 (0,0001) | -0,8682 (0,0001) |
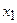
| -0,7039 (0,0001) | 1,0000 (0,0) | 0,9410 (0,0001) |
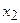
| -0,8682 (0,0001) | 0,9410 (0,0001) | 1,0000 (0,0) |
| В скобках: Prob > |R| under Ho: Rho=0 / N = 25 |
Коэффициент корреляции между 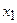 и
и 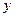 свидетельствует о значительной и статистически существенной обратной связи между прибылью кредитных учреждений, годовой ставкой по депозитам и числом кредитных учреждений. Знак коэффициента корреляции между прибылью и ставкой по депозиту имеет отрицательный знак, что противоречит нашим первоначальным предположениям, связь между годовой ставкой по депозитам и числом кредитных учреждений – положительная и высокая.
свидетельствует о значительной и статистически существенной обратной связи между прибылью кредитных учреждений, годовой ставкой по депозитам и числом кредитных учреждений. Знак коэффициента корреляции между прибылью и ставкой по депозиту имеет отрицательный знак, что противоречит нашим первоначальным предположениям, связь между годовой ставкой по депозитам и числом кредитных учреждений – положительная и высокая.
Если мы обратимся к исходным данным, то увидим, что в течение исследуемого периода число кредитных учреждений возрастало, что могло привести к росту конкуренции и увеличению предельной ставки до такого уровня, который и повлек за собой снижение прибыли.
Приведенные в таблице 3.3 линейные коэффициенты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии.
Таблица 3.3. Коэффициенты частной корреляции
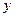
| 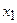
| 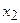
| |
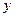
| 1,0000 (0,0) | 0,9265 (0,0003) | 0,0790 (0,8399) |
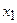
| 0,9265 (0,0003) | 1,0000 (0,0) | 0,0834 (0,8311) |
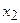
| 0,0790 (0,8399) | 0,0834 (0,8311) | 1,0000 (0,0) |
| В скобках: Prob > |R| under Ho: Rho=0 / N = 10 |
Коэффициенты частной корреляции дают более точную характеристику тесноты зависимости двух признаков, чем коэффициенты парной корреляции, так как «очищают» парную зависимость от взаимодействия данной пары переменных с другими переменными, представленными в модели. Наиболее тесно связаны 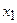 и
и 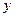 ,
, 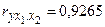 . Другие взаимосвязи существенно слабее. При сравнении коэффициентов парной и частной корреляции видно, что из-за влияния межфакторной зависимости между
. Другие взаимосвязи существенно слабее. При сравнении коэффициентов парной и частной корреляции видно, что из-за влияния межфакторной зависимости между 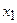 и
и 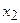 происходит некоторое завышение оценки тесноты связи между переменными.
происходит некоторое завышение оценки тесноты связи между переменными.
Результаты построения уравнения множественной регрессии представлены в таблице 3.4.
Таблица 3.4. Результаты построения модели множественной регрессии
| Независимые переменные | Коэффициенты | Стандартные ошибки | t - статистики | Вероятность случайного значения | ||
| Константа | 1,5645 | 0,0794 | 19,705 | 0,0001 | ||
| x1 | 0,2372 | 0,0556 | 4,269 | 0,0003 | ||
| x2 | -0,0002 | 0,00003 | -7,772 | 0,0001 | ||
| R2 = 0,87 | ||||||
| R2adj =0,85 | ||||||
| F = 70,66 | Prob > F = 0,0001 | |||||
Уравнение имеет вид:
y = 1,5645+ 0,2372 x1 - 0,00021 x2.
Интерпретация коэффициентов регрессии следующая:
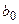 оценивает агрегированное влияние прочих (кроме учтенных в модели х1 и х2) факторов на результат y;
оценивает агрегированное влияние прочих (кроме учтенных в модели х1 и х2) факторов на результат y;
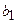 и
и 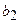 указывают на сколько единиц изменится y при изменении х1 и х2 на единицу их значений. Для заданного числа кредитных учреждений, увеличение на 1% годовой ставки по депозитам ведет к ожидаемому увеличению на 0,237% в годовом доходе этих учреждений. При заданном уровне годового дохода на один доллар депозита, каждое новое кредитное учреждение снижает норму прибыли для всех на 0,0002%.
указывают на сколько единиц изменится y при изменении х1 и х2 на единицу их значений. Для заданного числа кредитных учреждений, увеличение на 1% годовой ставки по депозитам ведет к ожидаемому увеличению на 0,237% в годовом доходе этих учреждений. При заданном уровне годового дохода на один доллар депозита, каждое новое кредитное учреждение снижает норму прибыли для всех на 0,0002%.
Значения стандартной ошибки параметров представлены в графе 3 таблицы 3.4: 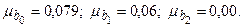 Они показывают, какое значение данной характеристики сформировалось под влиянием случайных факторов. Их значения используются для расчета t -критерия Стьюдента (графа 4)
Они показывают, какое значение данной характеристики сформировалось под влиянием случайных факторов. Их значения используются для расчета t -критерия Стьюдента (графа 4)
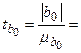 19,705;
19,705; 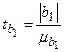 =4,269;
=4,269; 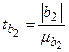 =-7,772.
=-7,772.
Если значения t -критерия больше 2, то можно сделать вывод о существенности влияния данного значения параметра, которое формируется под влиянием неслучайных причин.
Зачастую интерпретация результатов регрессии более наглядна, если произведен расчет частных коэффициентов эластичности. Частные коэффициенты эластичности 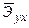 показывают, на сколько процентов от значения своей средней
показывают, на сколько процентов от значения своей средней 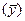 изменяется результат при изменении фактора xj на 1% от своей средней
изменяется результат при изменении фактора xj на 1% от своей средней 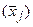 и при фиксированном воздействии на y прочих факторов, включенных в уравнение регрессии. Для линейной зависимости
и при фиксированном воздействии на y прочих факторов, включенных в уравнение регрессии. Для линейной зависимости 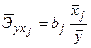 , где
, где 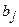 коэффициент регрессии при
коэффициент регрессии при 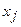 в уравнении множественной регрессии. Здесь
в уравнении множественной регрессии. Здесь
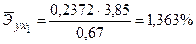
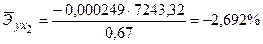
Нескорректированный множественный коэффициент детерминации 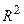 оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. В нашем примере эта доля составляет 86,53% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов. Иными словами, на весьма тесную связь факторов с результатом.
оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. В нашем примере эта доля составляет 86,53% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов. Иными словами, на весьма тесную связь факторов с результатом.
Скорректированный 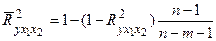 (где n – число наблюдений, m – число переменных) определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую детерминированность результата y в модели факторами x1 и x2.
(где n – число наблюдений, m – число переменных) определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую детерминированность результата y в модели факторами x1 и x2.
Для проведения дисперсионного анализа и расчета фактического значения F -критерия заполним таблицу результатов дисперсионного анализа, общий вид которой:
| Колеблемость результативного признака | Сумма квадратов | Число степеней свободы | Дисперсия | F-критерий |
| За счет регрессии | Сфакт. (SSR) | K |  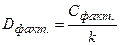 (MSR) (MSR)
| 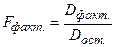
|
| Остаточная | Сост. (SSE) | n-(k+1) | 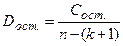 (MSE) (MSE)
| |
| Общая | Собщ. (SST) | n-1 |
Таблица 3.5. Дисперсионный анализ модели множественной регрессии
| Колеблемость результативного признака | Сумма квадратов | Число степеней свободы | Дисперсия | F-критерий |
| За счет регрессии | 0,40151 | 2 | 0,20076 | 70,661 |
| Остаточная | 0,06250 | 22 | 0,00284 | |
| Общая | 0,46402 | 24 |
Оценку надежности уравнения регрессии в целом, его параметров и показателя тесноты связи 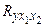 дает F -критерий Фишера:
дает F -критерий Фишера:
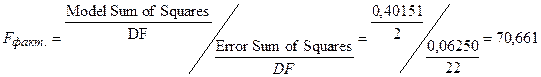
Вероятность случайного значения F - критерия составляет 0,0001, что значительно меньше 0,05. Следовательно, полученное значение неслучайно, оно сформировалось под влиянием существенных факторов. То есть подтверждается статистическая значимость всего уравнения, его параметров и показателя тесноты связи – коэффициента множественной корреляции.
Прогноз по модели множественной регрессии осуществляется по тому же принципу, что и для парной регрессии. Для получения прогнозных значений мы подставляем значения хi в уравнение для получения значения 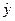 . Предположим, что мы хотим узнать ожидаемую норму прибыли, при условии, что годовая ставка депозита составила 3,97%, а число кредитных учреждений – 7115:
. Предположим, что мы хотим узнать ожидаемую норму прибыли, при условии, что годовая ставка депозита составила 3,97%, а число кредитных учреждений – 7115:
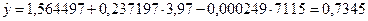 .
.
Качество прогноза – неплохое, поскольку в исходных данных таким значениям независимых переменных соответствует значение 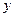 равное 0,70. Мы так же можем вычислить интервал прогноза как
равное 0,70. Мы так же можем вычислить интервал прогноза как 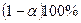 - доверительный интервал для ожидаемого значения
- доверительный интервал для ожидаемого значения 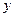 при заданных значениях независимых переменных:
при заданных значениях независимых переменных:
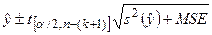 ,
,
где MSE – остаточная дисперсия, а стандартная ошибка 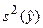 для случая нескольких независимых переменных имеет достаточно сложное выражение, которое мы здесь не приводим.
для случая нескольких независимых переменных имеет достаточно сложное выражение, которое мы здесь не приводим. 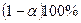 доверительный интервал для значения
доверительный интервал для значения 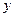 при средних значениях независимых переменных имеет вид:
при средних значениях независимых переменных имеет вид:
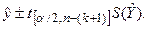
Большинство пакетов программ рассчитывают доверительные интервалы.
Дата публикования: 2015-10-09; Прочитано: 469 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
