Измерение вариации в уравнении регрессии

Для проверки того, как хорошо независимая переменная предсказывает зависимую переменную в модели, необходим ряд мер вариации. Первая мера - общая сумма квадратов (S_T) - есть мера вариации значений 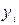относительно их среднего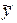

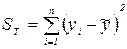(2.11).

В регрессионном анализе общая сумма квадратов может быть разложена на объясняемую вариацию (или сумму квадратов объясняемую регрессией) (S_R) и необъясняемую вариацию или остаточную сумму квадратов (S_E). Эти различные меры вариации отображены на рисунке:

Линия регрессии

y_i

					y=

Рис.5

Сумма квадратов, объясняемая регрессией, (S_R), основывается на разнице между средним значением зависимой переменной и значением этой же переменной, предсказанным по регрессионному уравнению:

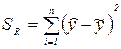(2.12).

Остаточная сумма квадратов (S_E) представляет часть вариации y, которая не объясняется регрессией. Она основывается на разнице между значениям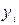и и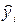

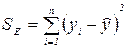(2.13).

Эти меры вариации могут быть представлены следующим образом:

S_T = S_R + S_E (2.14).

Из формулы (2.13) видно, что 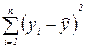- это выражение, стоящее под знаком корня в формулe (2.10) стандартной ошибки оценки. Компьютерные программы обычно вначале вычисляют значение сумму квадратов ошибки. В распечатке регрессионного уравнения, полученного на компьютере, 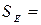468336,40896, общая сумма квадратов 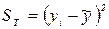= 513604,95000, а объясняемая вариация или сумма квадратов, объясняемая регрессией, 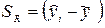= 468335,40896. Мы знаем, что S_T = S_R + S_E = 468335,40896 + 45269,54104 = 513604,95000

Отношение суммы квадратов отклонений, объясняемой регрессией, к общей сумме квадратов отклонений дает пропорцию изменения Y, объясняемого изменением X, и называется коэффициентом детерминации.

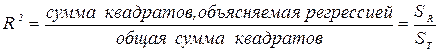(2.15).

Отсюда коэффициент детерминации - мера пропорции вариации, которая объясняется независимыми переменными в регрессионной модели.

Для нашего примера R² = 46,9145 /51,3605 = 0,9119

Следовательно, 91,19% вариации еженедельной выручки магазинов можно объяснить числом покупателей, варьирующим от магазина к магазину. Только 8,7% вариации можно объяснить иными факторами.

При построении уравнения регрессии для двух переменных мы объясняли взаимоотношения между ними как предсказание значений зависимой переменной Y по значениям независимой переменной X. С другой стороны мы знаем, что интенсивность взаимосвязи между двумя переменными измеряет коэффициент корреляции. Корреляционная связь может быть различного типа: положительная, отрицательная, либо отсутствовать. Сила корреляционной связи между двумя переменными в генеральной совокупности измеряется при помощи коэффициента корреляции, значения которого находятся в пределах от +1 для полной положительной корреляции до -1 при полной отрицательной корреляции.

Выборочный коэффициент корреляции можно определить как

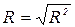(2.16).

В парной линейной регрессии R имеет тот же знак что и 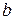_. Если 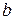положительно, то и 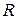положительно, если 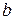отрицательно, то 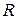- отрицательно, если 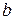рано нулю, то и 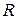равно нулю.

В нашем примере 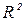= 0,913 и 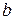- положительно, коэффициент корреляции R = 0,956. Близость коэффициента корреляции единице свидетельствует о сильной взаимосвязи между выручкой магазина и числом посетителей.

Хотя мы интерпретировали коэффициент корреляции в терминах регрессии, однако, как отмечалось выше, корреляция и регрессия - две различные техники. Корреляция устанавливает силу связи между признаками, а регрессия - форму этой связи. В ряде случаев для анализа достаточно найти меру связи между признаками, без использования одного из них в качестве предиктора для другого.

2.5. Интервал для прогноза оценки 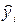и доверительный интервал генерального значения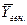

Поскольку в основном для построения регрессионных моделей используются данные выборок, то и интерпретация взаимоотношений между переменными в генеральной совокупности базируется на выборочных результатах.

Как мы уже говорили, регрессионное уравнение используется для прогноза значений Y по заданному значению X. В нашем примере мы уже показали, что, например, при 600 посетителях магазина сумма ожидаемая выручки 7661 усл. ден. ед. Однако это значение - только точечная оценка истинного среднего значения. Мы знаем, что для оценки истинного значения генерального параметра необходимо построение доверительного интервала. В случае с регрессионными параметрами, доверительный интервал для значений 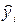, лежащих на линии регрессии, имеет вид:

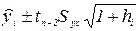(2.17),

где

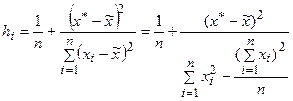(2.18),

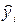- прогнозное значение зависимой переменной;

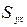- стандартная ошибка оценки;

n - объем выборки;

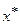- заданное значение .

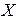Анализ выражения (2.18) указывает на то, что ширина интервала зависит от нескольких факторов. Для заданного уровня значимости увеличение вариации вокруг линии регрессии, как меры стандартной ошибки оценки, увеличивает ширину интервала. Однако, можно ожидать, что увеличение размера выборки сузит интервал. Более того, ширина интервала так же варьирует с различными значениями 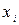. Когда оценивается 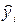по значениям 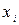близким к 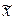, то интервал тем уже, чем меньше абсолютное отклонение 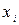от .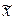

Когда оценка осуществляется по значениям 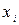, удаленным от среднего 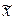, то длина интервала возрастает. Этот эффект виден из выражения под квадратным корнем в (2.17) и рисунке 6.

Y

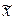Х

Рис.6.

Определим интервал оценки суммы реализации от пакетного молока в магазине, который посетят 600 покупателей:

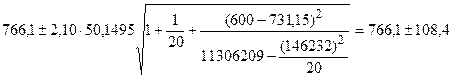
Следовательно, с 95% уверенностью можно утверждать, что ежедневная выручка отдельного магазина, который посетили 600 покупателей, находится в пределах от 657,7 до 874,5 усл.ден.ед.

Если мы хотим сделать вывод относительно выручки во всех магазинах, которые в среднем посещает 600 покупателей, то необходимо построить доверительный интервал для генерального среднего значения 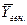при заданном X. Вариация в этом случае будет меньше, поскольку мы имеем дело не с отдельным, а со средним значением Y. Следовательно, интервал будет уже.

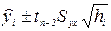(2.19)

2.6. Интервал для оценки истинных значений параметра уравнения регрессии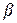

Построим доверительный интервал для оценки истинных значений неизвестного параметра уравнения регрессии 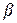. Для этого проверим гипотезу о равенстве нулю 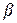. Сформулируем нулевую и альтернативную гипотезы:

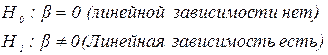
Если гипотеза будет отклонена, то подтверждается существование линейной зависимости между переменными Y и X. Для проверки гипотезы используется t -критерий (случайная величина, имеющая распределение Стьюдента с n-2 степенями свободы:

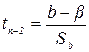, (2.20),

где

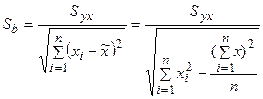(2.21).

Убедимся, что полученный выборочный результат является достаточным для заключения о том, что зависимость объема выручки от числа посетителей магазина существенна на 5% уровне значимости. Полученное значение 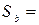0,0639, при наблюдаемом значении t -критерия

.

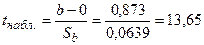По таблицам распределения Стьюдента найдем 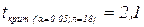, Распечатка решения, полученная на компьютере, сразу указывает нам, что вероятность того, что значение коэффициента 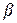равно нулю, очень мала – 0,0001.

Таким образом, мы можем отклонить нуль-гипотезу об отсутствии линейной зависимости переменных в пользу альтернативной гипотезы и предположить с высокой вероятностью, что линейная зависимость между ежедневной выручкой от реализации молока и числом посетителей магазина существует.