Оценка параметров модели парной регрессии. Расчет коэффициентов регрессии

Метод регрессионного анализа рассмотрим на следующем примере. Предположим, некоторая фирма торгует фасованными молочными продуктами и её интересуют ежедневные объемы продаж в магазинах города, например, литровых пакетов с молоком. Для выявления возможной взаимосвязи между числом покупателей в магазине и объемом реализации проведено обследование в 20 случайно выбранных магазинах города:

Таблица 2.1. Число покупателей и дневной объем продаж пакетного молока 20 магазинах города

Номер магазина	Число посетителей	Выручка (усл ден. ед.)

Данные, приведенные таблице, можно представить в более наглядном виде на точечной диаграмме (рис.2). Диаграмма наглядно показывает наличие положительной линейной взаимосвязи между числом посетителей магазина и выручкой от продажи молока, то есть можно предположить, что для приведенных данных будет адекватна модель вида (2.1): 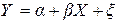где Х – число посетителей магазина, а Y – выручка от продажи.

Рис.2. Точечная диаграмма рассеяния данных о сумме выручки от продажи молока в различных магазинах города

Обращаясь к диаграмме, отметим, что через точки на графике можно провести несколько линий, удовлетворяющих выражению (2.1), а нам необходимо выбрать лишь одну, наилучшую.

При построении регрессионной модели мы, как правило, располагаем лишь выборочными данными, поэтому, полученные при подстановке данных коэффициенты регрессии будут лишь оценками истинных значений генеральных параметров модели.

Уравнение регрессии, полученное по выборочным данным, можно записать так

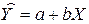(2.2),

где 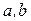- оценки истинных коэффициентов регрессии.

Следовательно, для каждого значения данных 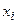существует фактическое (наблюдаемое) значение 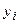, но при использовании выражения (2.2) появляется так же оценочное значение . Разность 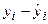-. это оценка ошибки, Чтобы не путать cо случайной ошибкой в модели истинной регрессии 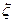, обозначим её 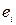и назовем остатком.

При статистической проверке взаимосвязи между X и Y необходимо найти такие оценки значений 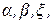в выражении (2.1), чтобы они были наилучшими, линейными и несмещенными (BLUE – Best, Linear, Unbiased Estimator).

Понятие наилучшие относится к требованию эффективности оценок параметров, то есть дисперсия оценок параметров должна быть наименьшей из всех возможных.

Термин линейность просто повторяет, что взаимосвязь линейна.

Несмещенность означает, что ожидаемые значения коэффициентов регрессии должны являться истинными коэффициентами.

Наиболее часто для нахождения параметров уравнения регрессии используется МНК, который дает наилучшие несмещенные оценки. Найденная с помощью МНК линия регрессии минимизирует сумму квадратов отклонений 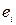, то есть . Это показано на рис. 3

Рис. 3

Проверка того удовлетворяют ли полученные с помощью МНК оценки параметров вышеуказанным условиям, проводится путем анализа остатков. Мы уже указывали, что в уравнении регрессии Y – случайная величина, следовательно, линейно связанная с ней ошибка 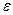- случайная величина, которая должна удовлетворять следующим условиям.

1. Нормальности

2. Гомоскедастичности

3. Независимости ошибок

(Этим же условиям должны удовлетворять Y-ки, однако анализ остатков модели более удобен).

Первое предположение – нормальности - требует, чтобы остатки 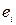были нормально распределены.

Второе условие – гомоскедастичности - требует, чтобы вариация вокруг линии регрессии была постоянной для всех значений 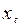. Это означает, что вариация 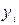, а, следовательно, и 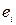имеет одни и те же значения и в случаях, когда 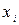имеет наибольшие значения, и в случаях, когда 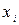мало. Если оно нарушается, то мы говорим о гетероскедастичности модели. Это условие очень важно для использования МНК для определения коэффициентов регрессии.

Третье условие независимости ошибок требует, чтобы ошибки (“остатки” - разность между теоретическими и эмпирическими значениями) были независимы для каждого значения Х. Это условие часто относится к данным, которые собираются за некоторый период времени. Например, данные, собранные за какой-нибудь период, могут коррелировать с данными за предыдущий период, в этом случае мы говорим, что данные автокоррелированы.

Так как Y – случайная величина, в случае линейной зависимости для любых значений X значения Y будут нормально распределены и таким образом, статистическое распределение 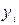может быть полностью описано при помощи средней и дисперсии:

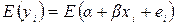(2.3).

Так как 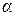и 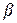- постоянны, а 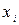- нестохастична, это выражение преобразуется в

(2.4).

Однако поскольку математическое ожидание 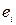равно нулю, то выражение (4) превращается в

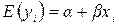(2.5).

Так как математическое ожидание 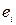равно нулю, то дисперсия 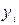, которая служит так же дисперсией 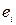равна

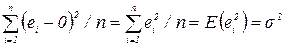(2.6),

то есть дисперсия 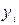равна среднему значению квадратов остатков модели.

Отсюда 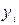нормально распределено с параметрами . Это показано на рисунке 4.

Рис. 4

Для предсказания значений Y нам необходимо определить два коэффициента 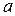- свободный член уравнения и 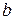- наклон линии регрессии. После того как они будут определены, линия регрессии может быть перенесена на график. Мы сможем визуально оценить насколько хорошо наша статистическая модель подогнана к реальным данным. Мы можем увидеть близки ли выборочные данные к линии регрессии или значительно отклоняются от нее.

В настоящее время решение регрессионных уравнений, как правило, проводится с помощью специализированных компьютерных программ.

Величины, минимизирующие суммы квадратов отклонений 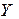от для случая парной регрессии, находятся следующим образом:

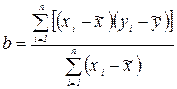(2.7)

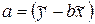(2.8)

Значения ошибок, называемые обычно остатками, рассчитываются как

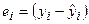(2.9)

Используя данные примера, получим следующее уравнение для “лучшей” линии регрессии:

.

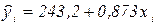Наклон линии регрессии 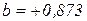. Это означает, что при увеличении Х на единицу ожидаемое значение Y возрастет на 0,873 единицы. То есть регрессионная модель предсказывает, что каждый новый посетитель магазина в среднем увеличивает ежедневную сумму реализации молока на 0,873 условных денежных единиц (или мы можем сказать, что мы можем ожидать прирост ежедневной реализации на 87,3 денежных единицы, если привлечем в магазин добавочно 100 посетителей). Отсюда, наклон может быть рассмотрен как прирост дневных продаж, который оценивается варьирующими относительно числа посетителей магазина.

Свободный член уравнения получился равным +243,2 условных денежных единицы. Свободный член представляет значение Y при Х равном нулю. Поскольку мало вероятно число посетителей магазина равное нулю, то мы можем интерпретировать Y как прирост дневной выручки, который варьирует с другими факторами (не с числом посетителей).

Регрессионная модель может быть использована для прогнозирования суммы ежедневной реализации молока. Например, нас интересует прогноз реализации молока в магазинах, которые посещают по 600 покупателей в день. Подставим x_i = 600 в наше регрессионное уравнение:

.

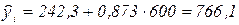Отсюда прогнозируемая дневная выручка для магазина с 600 посетителей равна 766,1 условных денежных единиц.

При прогнозировании значений зависимой переменной по уравнению регрессии, важно помнить, что нам доступны только те значения независимых переменных, которые находятся в интервале от наименьших до наибольших значений, использованных при создании модели. Отсюда, когда мы предсказываем Y по заданным значениям Х, мы можем интерполировать значения в пределах заданных рангов, но мы не можем экстраполировать вне рангов значений Х. Например, когда мы используем число посетителей для предсказания дневной выручки магазина, то мы знаем из данных примера, что их число находится в пределах от 420 до 1010. Следовательно, предсказание дневной выручки может быть сделано только для магазинов с числом покупателей в пределах от 420 до 1010 человек.