Виконання студентами тестових завдань з питань теми заняття. Ключовими термінами, на розумінні яких базується засвоєння навчального матеріалу теми, є : функція і щільність розподілу залишкового часу життя

Методичні вказівки

Ключовими термінами, на розумінні яких базується засвоєння навчального матеріалу теми, є: функція і щільність розподілу залишкового часу життя, моделі страхування життя, характеристики підсумкового ризику.

З метою глибокого засвоєння навчального матеріалу при самостійному вивченні теми студенту варто особливу увагу зосередити на таких аспектах.

Одна з теоретичних основ страхового бізнесу – актуарна математика (актуарій у перекладі з англійської – це статистик страхового товариства.

Вкажемо на основні задачі страхової математики.

1) Визначення розумного співвідношення між премією p і виплатою в (p<<b).

2) Розрахунок ймовірності розорення p (S>U), де U –капітал компанії, а S = 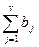– сума її виплат.

3) Розрахунок резервів страхової компанії.

Нехай X – тривалість життя (випадкова величина). Позначимо через X_і тривалість життя і -го індивідуума (і= 1,2 ,…, п). В актуарній математиці для характеристики величини Х використовуюься функція розподілу F (x)= p (X≤ x) і функція виживання s(x):

s (x) =p (X>x) =1-F (x).

Функція s (x) – це ймовірність того, що людина доживе до віку x років (індивідуума віку x позначають (x)).

Функція f (x) =F' (x) =-s' (x), яка є щільністю розподілу випадкової величини X, носить назву крива смертей.

Аналітичні моделі тривалості життя

Графік функції виживання, побудований на основі статистичних даних, представляє собою емпіричну ламану лінію, яку “згладжують”, підбираючи підходящу аналітичну формулу.

Наведемо кілька способів такої апроксимації, а саме: моделі де Муавра, Гомпертца, Мейкхама, Вейбулла, Ерланга.

Модель де Муавра. У 1729 р. А. Муавр запропонував вважати, що тривалість життя розподілена рівномірно на інтервалі (0; w), де w – граничний вік. Для цієї моделі при 0< х < w маємо:

f (х)=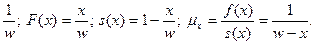

Ця модель проста, але не досить точна.

Модель Гомпертца (1825 р.). У цій моделі інтенсивність смертності задається формулою

µ_х=Ве^αх,

де α >0, В >0 – деякі параметри. Знайдемо функцію виживання: 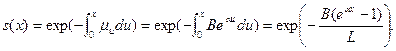Щільність кривої смертей визначаємо за формулою

f (x) =µ_хs (x) =Bexp .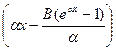

Неважко перевірити, що ця крива має у деякій точці максимум і, отже, краще відображає поведінку емпіричних кривих.

Модель Мейкхама (1860р.). Ця модель вдосконалює модель Гомпертца і враховує не лише вплив віку на смертність, але і ризики для життя, пов’язані з нещасними випадками (ці ризики практично не залежать від віку). Інтенсивність смертності µ_х у цій моделі наближають функцією виду

µ_х=А+В ,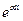

де А, α, В – деякі додатні числа, причому параметр А враховує ризики, пов’язані з нещасними випадками, а доданок В 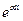враховує вплив віку на смертність.

При цьому

s(x)=exp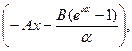

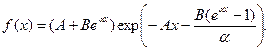
Закон Мейкхама враховує, що у малому віці головну роль у смертності відіграють нещасні випадки, а при збільшені віку їх роль зменшується.

Модель Вейбула (1939р.).

Для інтенсивності смертності було запропоновано використовувати степеневу функцію µ_х=kxⁿ, яка теж має максимум.

При цьому s (x)= exp .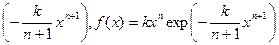

Модель Ерланга. У випадку моделі Ерланга 2-го порядку крива смертей задається формулою

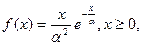
де α> 0 – фіксований параметр.

У цьому випадку функція виживання

s (x)=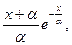

а інтенсивність смертності µ_{х= 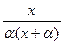.} Крива смертей має максимум (правда, зміщений вліво по відношенню до емпіричного максимуму).

За допомогою аналітичних моделей зручно розраховувати ймовірнісні характеристики тривалості життя.

Загальноприйнятими є такі позначення:

1) _tq_x – ймовірність смерті людини віком x років у проміжку часу (x,x+t ]:

_tq_x = P (T (x)≤ t)= .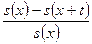

2) _tp_x (або _tx) – ймовірність протилежної події, тобто ймовірність того, що людина віком x років проживе ще, як мінімум t років:

_tp_x=P (T (x)> t)=1- _tq_x= .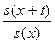

При t= 1 (найважливіший для актуарної математики випадок) передній індекс t= 1 у наведених позначеннях опускають. Таким чином, одержуємо:

q_x=P (T (x)≤ 1) =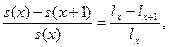

p_x=P (T (x)> 1)= .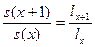

При цьому q_x= 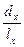(зауважимо, що q_x – одна з основних характеристик, які входять у ТТЖ).

3) _t/uq_x – ймовірність того, що людина віком x років проживе ще t років, але помре протягом наступних u років:

_t/uq_x=P (t< T (x)≤ t+u).

Зауважимо, що цю ймовірність можна виразити через

_tq_x, _tp_x або через s (x):

_t/uq_x=P (T (x) ≤t+u)- P (T (x) ≤t)= _{t + u}q_x- _tq_x;

_t/uq_x=P (T (x) >t)- P (T (x) >t+ u)= _tp_x- _t+up_x;

_t/uq_x= _t+uq_x- _tq_x=

=

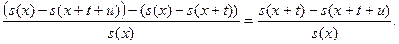
Якщо u =1, то цей індекс опускають. У такому випадку маємо:

_t/q_x= _{t+ 1} q_x- _tq_x= _tp_x- _{t+ 1} p_x= .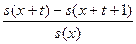

4) 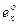– середнє значення залишкового часу життя Т (х) людини віком х років, або повна ймовірна тривалість життя такої людини: 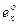= МТ(х).

Можна довести, що 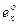= 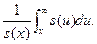При цьому дисперсія DТ (х) обчислюється за формулою:

DТ (х)=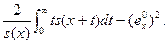

Припустимо, що компанія уклала N договорів страхування, а ξ_k (k = 1, 2,… N) – індивідуальні позови за цими договорами.

Суму S 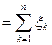називають підсумковим ризиком.

Якщо S≤ u, де u – капітал компанії, то ця страхова компанія зможе виконати свої зобов’язання перед клієнтами. У противному випадку йдеться про розорення компанії. Ймовірність розорення компанії R, що визначається формулою R = P (S>u), дорівнює значенню додаткової функції розподілу підсумкового ризику в точці u.

Індивідуальні позови ξ_k, як правило, є незалежними величинами. Розподіл підсумкового ризику знаходять за допомогою відомих ймовірнісних методів. Так, якщо ξ₁, ξ₂ – незалежні випадкові величини, які можуть приймати невід’ємні цілочислові значення, користуються формулою згорток.

Іншим точним методом розрахунку характеристики підсумкового ризику є метод твірних функцій.

Методи Гаусса і Пуассона – відомі наближені методи розрахунку підсумкового ризику.

Семінарське заняття 8

Тема 11. Методи аналізу і прогнозу

Питання для усного опитування та дискусії

11.1. Прогнозування фінансових показників з використанням математичного моделювання.

11.2. Метод парних порівнянь.

11.3. Нечітко – множинні методи оцінки ризику.

Аудиторна письмова робота