Показатели надежности восстанавливаемых объектов

Для того чтобы найти показатели, характеризующие надежность восстанавливаемого объекта, необходимо определить модель его функционирования.

Простейшей является такая модель, при которой объект какое-то случайное время t₁ работает до первого отказа, фиксируемого достоверно, затем следует мгновенное и полное восстановление свойств элемента в момент t₁ = t₁, после чего элемент снова работает случайное время t₂ до второго отказа, определяемого достоверно, затем мгновенно восстанавливается до начального состояния в момент t₂ = t₁ + t₂ и так далее. Для определенности полагают, что в начальный момент времени элемент работоспособен (рис. 3).

Моменты отказов t₁, t₂,..., t_i,..., t_m образуют случайный поток (или процесс) отказов, а так как восстановление следует мгновенно, то эти же моменты образуют случайный поток (или процесс) восстановления.

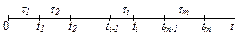
Рис. 3. Модель функционирования мгновенно восстанавливаемого элемента

Суммарная наработка до возникновения m- го отказа равна:

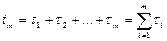. (18)

Возможны два пути оценки надежности восстанавливаемых объектов:

1) вычисление характеристик потока отказов;

2) вычисление условных распределений наработки между отказами.

Процесс восстановления можно описать случайной величиной r (t), равной числу отказов, происшедших за время t. Естественно, что r(t) принимает только целые неотрицательные значения. Величину r(t) можно характеризовать математическим ожиданием числа отказов, происшедших на интервале (0, t):

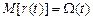, (19)

которое обычно называют ведущей функцией потока отказов или функцией восстановления. Часто удобно использовать функцию

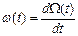, (20)

которую называют плотностью восстановления (отказов) или параметром потока восстановления (отказа).

Параметр потока отказов – это отношение среднего числа отказов восстанавливаемого объекта за произвольно малую его наработку к значению этой наработки.

Случайная величина r(t) имеет распределение с законом

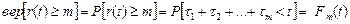, (21)

где F_m(t) – закон распределения случайной величины t_m.

Вероятность того, что за время t не будет ни одного восстановления (отказа):

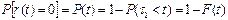, (22)

где F(t) = F₁(t) – вероятность первого отказа.

В общем случае вероятность того, что за время t будет ровно т восстановлений (отказов), определяется зависимостью:

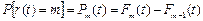. (23)

По определению математического ожидания имеем:

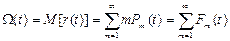. (24)

Соответственно

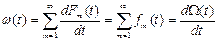, (25)

где f _m(t) – плотность вероятности случайной величины t_m.

В статистической форме:

, (26)

где n(t_i) – количество отказов, зафиксированное по истечении t_i.

Для случая экспоненциального закона распределения времени между восстановлениями или отказам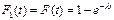и:

и .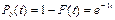

Процесс восстановления является пуассоновским потоком, для которого вероятность получения ровно т восстановлений (отказов)

, (27)

где l t – математическое ожидание числа восстановлений (отказов) на интервале (0, t), т. е.

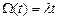. (28)

Тогда

. (29)

Таким образом, для экспоненциального закона плотность восстановления (или параметр потока отказов) численно равна интенсивности отказов l невосстанавливаемого, работающего до первого отказа элемента.

Часто бывает важным установить асимптотические свойства процесса восстановления – его характеристики при большом времени t, после того как наблюдалось большое количество отказов при произвольном законе F(t). Можно показать, что

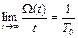. (30)

Из формулы видно, что для длительного участка времени t среднее число отказов, приходящихся на единицу времени, является величиной, обратной среднему времени жизни элемента.

Следовательно, если рассматривать стационарный процесс, то часть формул упростится.

Средняя наработка между отказами восстанавливаемого изделия:

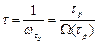. (31)

А с учетом (29):

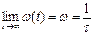. (32)

Полученные выше зависимости справедливы для простейшего процесса восстановления (мгновенное и полное восстановление свойств элемента при достоверно фиксируемом отказе). На практике время восстановления имеет конечные случайные значения, зависящие как от свойств элемента, так и от характеристик персонала, ведущего восстановление, организации работ, наличия запасных элементов и других объективных и субъективных факторов.

Представим модель функционирования элемента (рис. 4) в следующем виде: работоспособный в момент t = 0 элемент функционирует в течение случайного времени t₁ до первого отказа, фиксируемого достоверно в момент t₁ = t₁, затем в течение случайного времени t_1в восстанавливается полностью до состояния, в котором находился в момент t = 0, и работает случайное время t₂ до второго отказа, фиксируемого достоверно в момент t₂ = t₁ + t_1в + t₂, затем восстанавливается за случайное время t_2в до начального состояния и так далее. Моменты

(33)

составляют поток отказов, а моменты

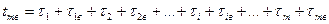(34)

образуют поток восстановлений элемента (причем m = 1, 2, …).

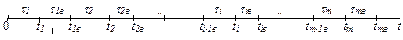
Рис. 4. Модель функционирования элемента, восстанавливаемого за конечное время

Будем полагать, что все случайные величины t_i = t и t_iв = t_в (i = 1, … m) независимы.

Кроме того, у всех t_i = t одинаковый закон распределения F(t) = Р(t < t) с математическим ожиданием М[t] = T₁ и СКО s₁ = ÖD[t], а также все величины t_iв = t_в распределены одинаково с законом G(t) = Р(t_в < t) с математическим ожиданием М[t_в] = T₂ и СКО s₂ = ÖD[t_в].

С использованием приведенных функций запишем формулы для определения некоторых параметров для времени восстановления объекта.

Среднее время восстановления объекта:

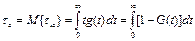(35)

или в статистической форме

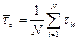. (36)

Интенсивность восстановления объекта в момент времени t, отсчитываемый от момента начала восстановления:

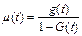(37)

или в статистической форме

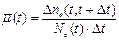, (38)

где 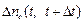– число восстановлений в интервале времени [t, t + Dt]; 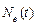– число объектов, еще не восстановленных к моменту t; Dt – длина интервала.

Важнейший показатель надежности такого элемента – коэффициент готовности К_г(t), представляющий собой вероятность того, что элемент окажется работоспособным в произвольный момент времени t.

В практических задачах обычно используют стационарное значение коэффициента готовности K_г, к которому стремится функция K_г(t) при t ® ¥. Можно показать [5], что

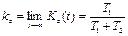, (39)

где Т₁ и Т₂ – математическое ожидание времени отказа и времени восстановления соответственно.

Если длительность безотказной работы и длительность восстановления распределены по экспоненциальным законам, то:

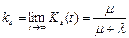. (40)