Понятие волны. Уравнение плоской волны. Волновое уравнение

В предыдущем семестре нам удалось уяснить причину возникновения волнового движения [3, с. 36 со второго абзаца, с. 37, 38 со второго абзаца] – упругая деформация в сплошных средах передаётся последовательно от одной точки среды к другой. Рассмотрение упругих колебаний в кристалле, параграф 6.1, оказалось успешным, потому что мы могли трактовать тепловые возбуждения в нём как газоподобную систему, состоящую из независимых частицеподобных объектов. Успех был связан с тем, что мы можем мысленно расчленять макроскопический объект на физически малые элементы объёма. При этом элемент сплошной среды может играть роль «частицы», за взаимодействием и движением которой мы в состоянии наблюдать на опыте. Поэтому подход к рассмотрению обозначенных в данном параграфе вопросов в модели «размазанного» по некоему объёму вещества неизбежен.

Простейшим движением в сплошных средах является распространение упругой деформации, возникающей под действием внешней силы. Действительно, возникшие при деформации упругие силы стремятся вернуть элементы среды к первоначальному состоянию равновесия; благодаря взаимодействию между соседними элементами среды упругие деформации будут передаваться от одних участков среды к другим, более удалённым от начального возбуждения. Очевидно, что это движение устанавливается не сразу и внешняя сила должна действовать периодически, например, по закону F = F _o×sin wt. Распространяющиеся по кристаллу (сплошной среде) вынужденные колебания называются бегущей упругой волной в противоположность стоячей упругой волне. В зависимости от характера возникающих при этом деформаций различают продольные волны (в жидкостях, газах и твёрдых телах) – частицы среды колеблются вдоль линий распространения колебаний и поперечные (в твёрдых телах?)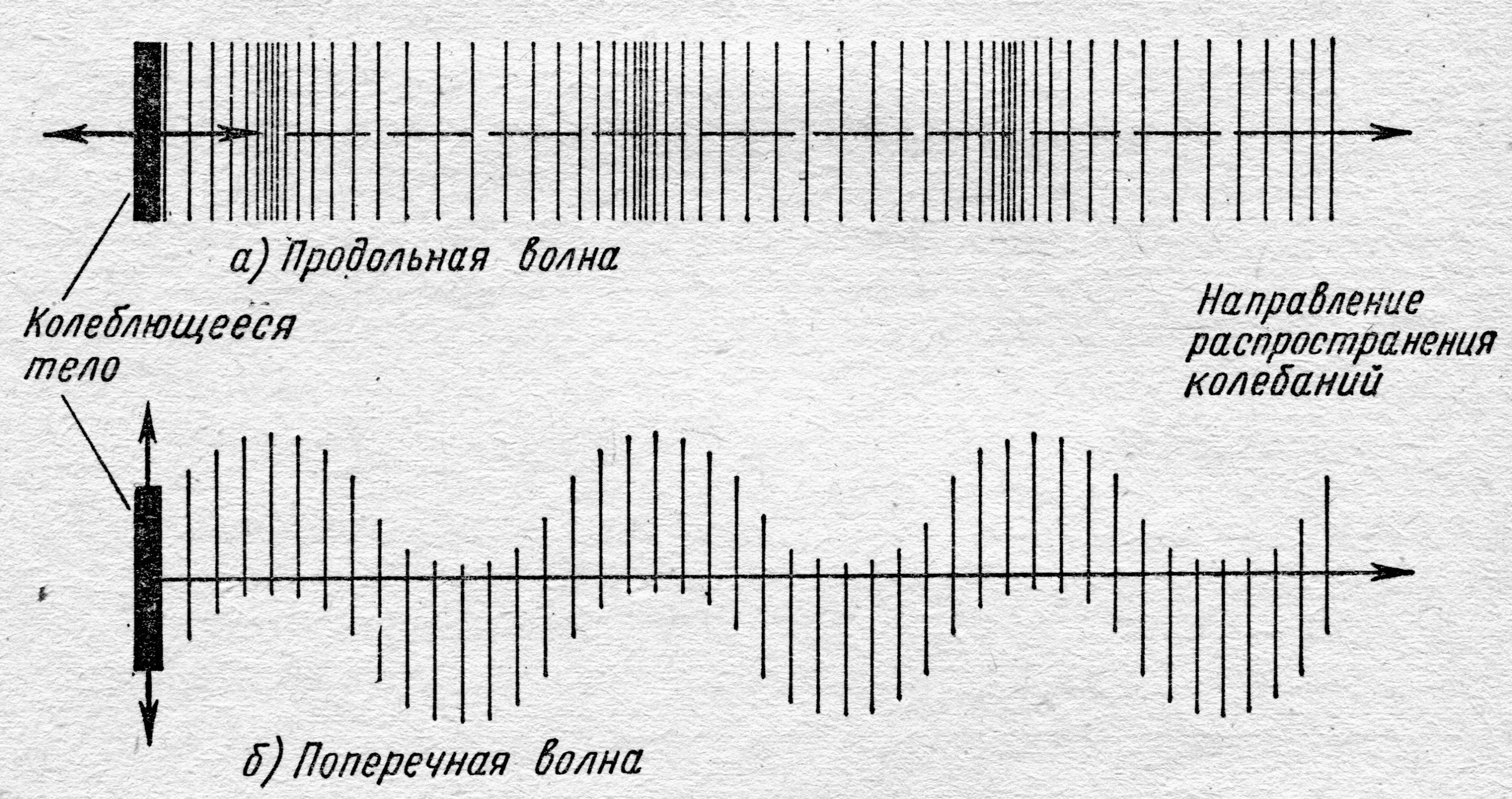

Рис. 6.4. Процесс распространения упругих деформаций в сплошных среда х

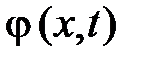
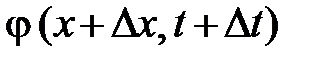
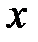
– частицы среды колеблются перпендикулярно направлению распространения волны (рис. 6.4.).

Бегущая волна отличается от стоячей. В частности, фаза колебаний двух разных элементов (квазичастиц) сплошной среды, по которой распространяется бегущая гармоническая волна, не совпадает с фазой этих же элементов в стоячей волне, отвечающей той же самой частоте (моде) колебаний. В стоячей волне все частицы, участвующие в данной моде (колебании), осуществляют колебания, обладая одной и той же фазой. В бегущей же волне всё обстоит иначе. Если колеблющийся элемент находится дальше от края, к которому приложена вынуждающая сила (рис. 6.4), то он будет совершать абсолютно такое же движение, что и ближайшие частицы, но в более поздний момент времени D t. Этот промежуток времени необходим для того, чтобы возбуждение (бегущая волна) прошло это расстояние. Найдём связь между состояниями колебательного движения в различных точках среды.

Будем искать закон движения бегущей волны в виде: y _бег (х, t) = = y _o×sin j (х, t), где величина j (х, t) = w t – d× х называется фазой бегущей гармонической волны. Неизвестную d-дельта определим из условия совпадения фаз колебаний частиц среды j _х = j _{х +Dх} в точке х и в точке х +D х (рис. 6.4), до которой распространится возбуждение (уплотнение) к моменту времени t +D t. Тогда, сравнивая аргументы функций y _бег(х, t) и y _бег(х +D х, t +D t), приходим к равенству:

j (х, t) = (w t – d х) = j (х +D х, t +D t) = w (t +D t) – d×(х +D х). (6.1)

Поскольку j _х = j _{х +Dх}, разность фаз должна равняться нулю:

Dj = j _{х +Dх} – j _х = 0

и пытливый студент, проделав преобразования, из равенства (6.1) приходит к выражению вида: [ w (t +D t) – d×(х +D х)] – (w t – d х) = 0, откуда немедленно следует, неизвестная величина d-дельта равна:

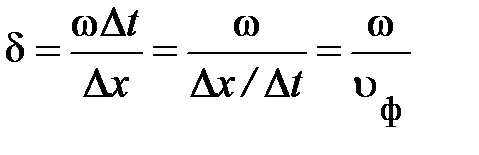. (6.2)

Здесь 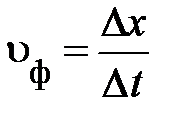– скорость распространения возбуждения или фазовая скорость бегущей волны (скорость распространения одного и того же значения фазы, j (х, t) = const, вынужденных колебаний); D t – время запаздывания колебания в точке (х +D х) (рис. 6.4); w – циклическая частота колебаний в сплошной среде, вызванных внешним воздействием на неё.

С учётом (6.2) закон движения бегущей волны примет вид:

y _бег (х, t) = y _o×sin(w t – 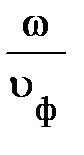× х). (6.3)

Обсудим некоторые свойства бегущей волны. Нетрудно видеть, и это следует из уравнения (6.3), что при t = const у _бег (х) является периодической функцией х. Действительно, если учесть, что циклическая частота w = 2p/T, уравнение волны приобретает вид:

у _бег (х) = y _o×sin();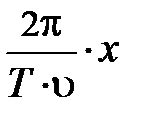

здесь t = 0; знак «–» можно опустить, поскольку здесь он лишь подчёркивает запаздывание колебаний в удалённых точках сплошной среды.

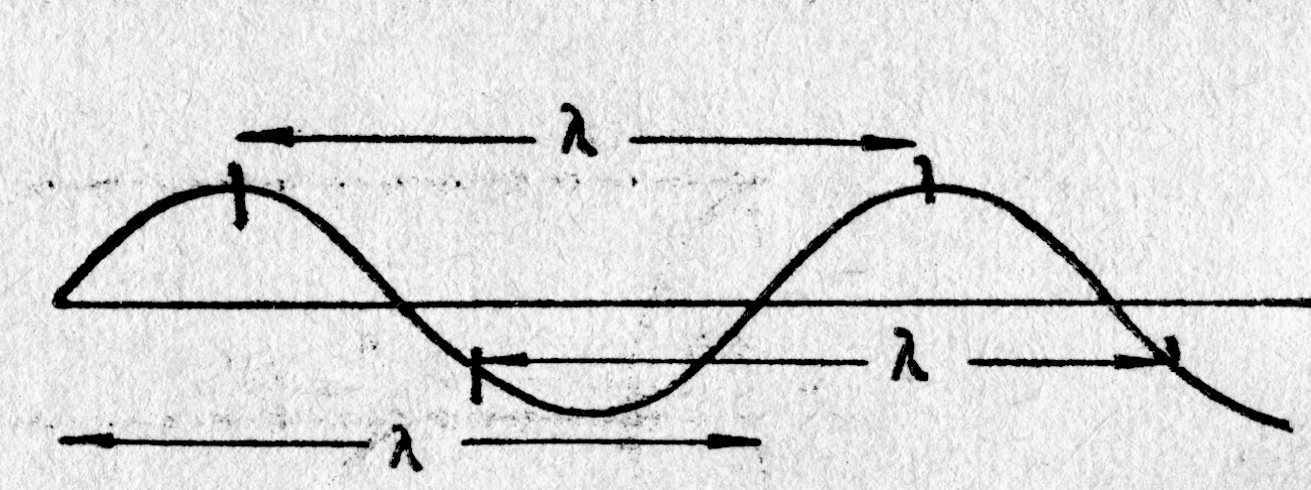
Из вида представленного уравнения следует, период этой синусоиды в пространстве равен произведению u× Т = l. Этот пространственный период, т. е. расстояние, через которое повторяется волнообразное распределение в среде (рис. 6.5), носит название длины волны. С ним мы познакомились в работе [3, с. 39]. Таким образом, мы получили известное соотношение, связывающее скорость движения волны с длиной волны и периодом колебания точки.

При х = const уравнение волны приобретает вид:

у _бег (t) = y _o×sin w t,

и, являясь периодической функцией t, отражает колебательный процесс частиц в данной точке среды.

Здесь уместно заметить, при волновой передаче деформации через среду по закону синуса меняется ряд физических величин: смеще

Рис.6.5. Пространственная повторяемость волнообразного распределения

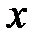ние точки от положения равновесия, скорость колеблющихся частиц, давление, плотность. Поэтому уравнение волны, которым мы оперируем, является весьма общим. Под символом функции у может быть любая из перечисленных физических величин, изменяющихся по закону синуса при движении волны вдоль направления х. Правда, не все физические величины обязаны быть в одной фазе.

В формуле бегущей волны (6.3) колеблющаяся величина зависит от двух изменяющихся параметров: положения в пространстве среды х и времени t. Найдём частные производные от функции y _бег (х, t) по времени при постоянном х:

= u = y _ow×cos w(t – x /u), (6.4а)

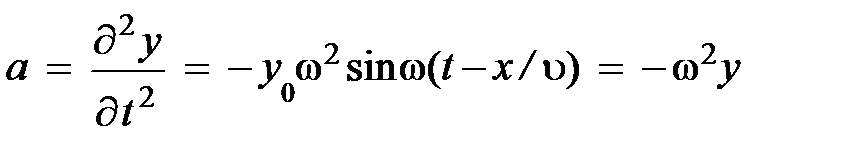. (6.4б)

Если у – смещение частиц среды при колебаниях, то u и а будут скоростью и ускорением этих частиц при их колебательном движении в точке с координатой х, т. е. 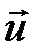характеризует быстроту изменения смещения частицы, а ускорение 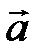– быстроту изменения 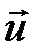за единицу времени.

Из уравнений (6.4) следует связь между амплитудными значениями этих величин:

u ₀ = y ₀×w, a ₀ = y ₀×w² = u₀×w.

Частные производные от функции y _бег (х, t) по х при t = const запишутся:

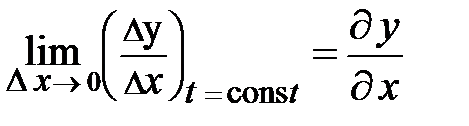= y _o 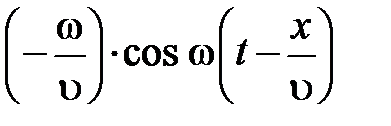, (6.5 а)

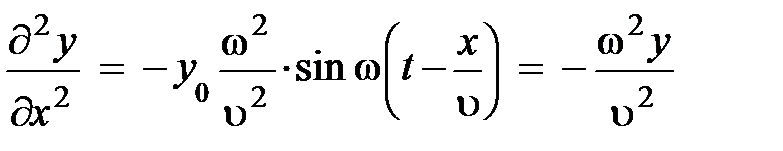. (6.5 б)

Поскольку y есть смещение частиц среды при колебаниях, то производная по х, при постоянном t, показывает изменение значения колеблющейся величины у на единицу расстояния между точками среды D х = х₂ – – х₁. Другими словами, как увеличивается или уменьшается у вдоль оси х в данный момент времени. Пытливый читатель может на рисунке, подобном (рис. 6.5), выбрать две точки на оси х и увидеть, как изменяется смещение y частицы при колебаниях на расстоянии D х.

В заключение параграфа следует обратить внимание на частные производные второго порядка, уравнения (6.4 б) и (6.5 б). Из уравнений следует, изменения в движении квазичастицы в данной точке среды (6.4 б) могут быть связаны с изменениями в движении квазичастицы, обусловленными её пространственным расположением (6.5 б). Действительно, если в правую часть уравнения (6.5 б) подставить левую часть уравнения (6.4 б), немедленно приходим к уравнению, связывающему быстроту изменения в движении квазичастицы, обусловленную её пространственным движением, с быстротой изменения в движении частицы, связанную со временем:

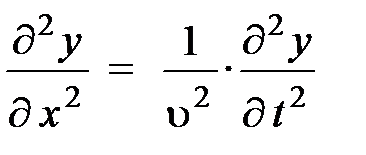. (6.6)

Это дифференциальное уравнение плоской гармонической волны, распространяющейся по оси Х, называется волновым уравнением. Несмотря на то, что волновое уравнение получено нами из уравнения волны (6.3), можно сделать и обратное заключение – если физическая величина у = у (х, t) зависит от времени и координат так, что её частные производные удовлетворяют уравнению (6.6), то величина у распространяется в среде в виде плоской волны.

И ещё один факт следует отметить, уравнение (6.5 б) не содержит времени и с учётом того, что w = 2p/T, а u = l / Т принимает вид:

. (6.7)

Итак, на первый взгляд нам удалось найти наиболее пригодную физическую модель для описания движения в континуальной физике – это бегущая волна вида: . Она играет в сплошной среде такую же роль, какую в корпускулярной физике играет модель частицы.

Из наших рассуждений следует, особенностью элементов сплошной среды как «частиц» является то, что они могут двигаться независимо. Любое их движение должно быть таким, чтобы не разрушить целостность среды. Нам удалось в этом убедиться на уровне общих слов в работе [3, с. 44, 45]. Чтобы найти подтверждение качественному своеобразию упругих волн, следует обратиться к вопросу об энергии бегущих упругих волн.