Сложение взаимно перпендикулярных колебаний

В предыдущем параграфе рассматривалась колебательная система, обладающая одной степенью свободы: отклонение системы от состояния равновесия определялось координатой х (или углом отклонения j). Движение точки на плоскости требует описания уже двумя уравнениями (двумя функциями): х = х (t) и у = у (t). Если эти функции представляют собой гармонические колебания

х = а ×sin wt, у = b ×sin (wt + a), (5.10)

где a – разность фаз обоих колебаний, перед нами стоит задача проследить за закономерностями сложного колебания, являющегося суммой двух взаимно перпендикулярных гармонических колебаний одной и той же частоты w.

Уравнения (5.10) представляют собой заданное в параметрической форме уравнение траектории на плоскости, по которой движется тело, участвующее в обоих колебаниях. Чтобы выяснить характер результирующей траектории движения, надо получить уравнение траектории в обычном виде, т. е. через координаты на плоскости х, у и разность фаз колебаний a. Для этого нужно исключить из уравнений (5.10) параметр времени t и найти уравнение f (х, у) = 0.

Запишем уравнения смещений (5.10) в виде

.

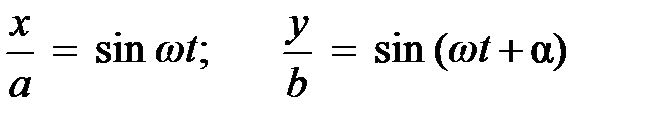Опираясь на тригонометрическое тождество (5.2), «развернём» синус суммы во втором из уравнений. После этого уравнение принимает вид:

.

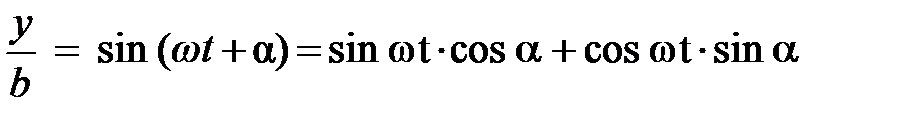В правой части вновь полученного уравнения, sin wt можно заменить отношением х / а. Для исключения временного параметра в функции cos wt, воспользуемся тем, что сумма квадратов синуса и косинуса равна единице, т. е. sin² wt + cos² wt = 1. И тогда:

.

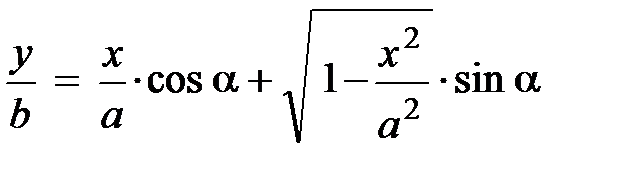Наконец, оставив в правой части радикал и собрав всё остальное в левой части, возведём левую и правую части равенства в квадрат. После выполнения этой операции и несложных преобразований пытливый и настойчивый читатель приходит к уравнению:

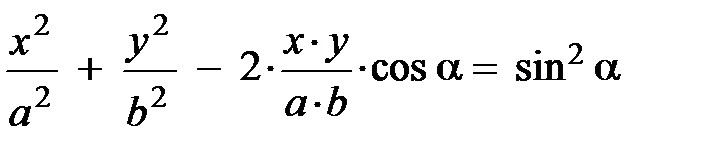. (5.11)

Из аналитической геометрии известно, уравнение (5.11) является уравнением эллипса. Ориентация эллипса и величина его полуосей «чувствительны» к амплитудам а и b и разности фаз a. Исследуем форму траектории в некоторых частных случаях.

Разность фаз a = 0. Уравнение (5.11) принимает вид:

,

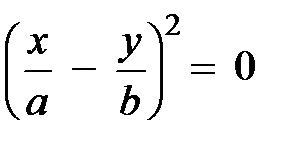откуда немедленно получается уравнение прямой:

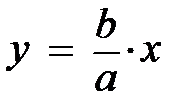. (5.12)

Рис. 5.4. Сложение взаимно перпендикулярных колебаний a = 0

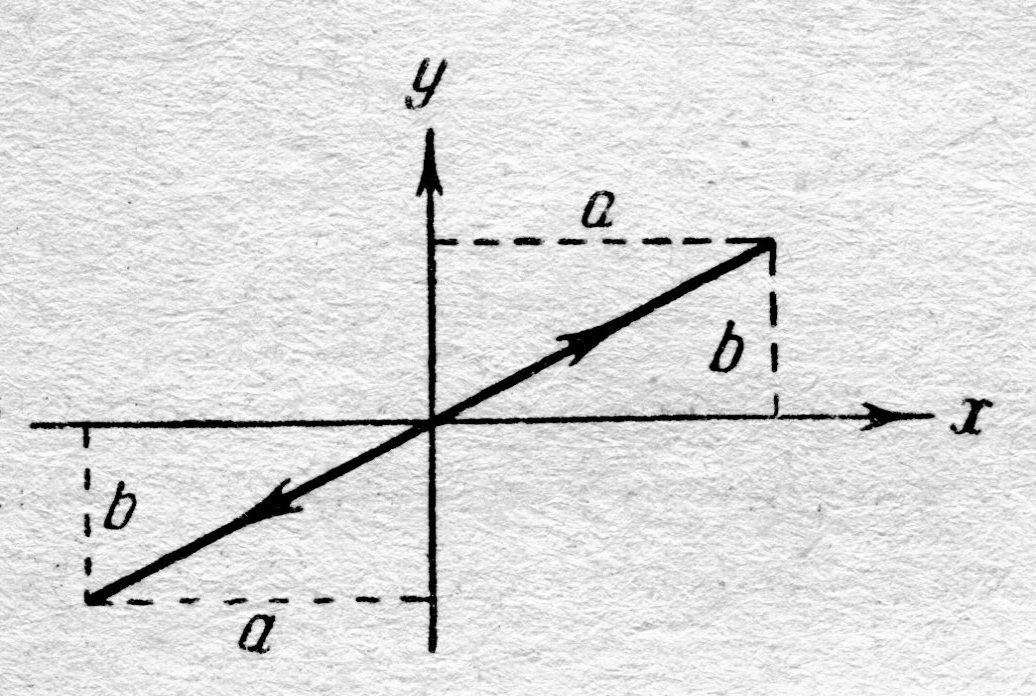Колеблющаяся точка перемещается по этой прямой, а её расстояние от начала координат . Отсюда следует, результирующее движение является гармоническим колебанием вдоль прямой (5.12) с частотой w и амплитудой 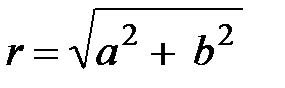(рис. 5.4). При подстановке уравнений (5.10) под радикал учтено, a = 0. Таким образом, при разности фаз складываемых колебаний, равной нулю, эллипс вырождается в прямую линию.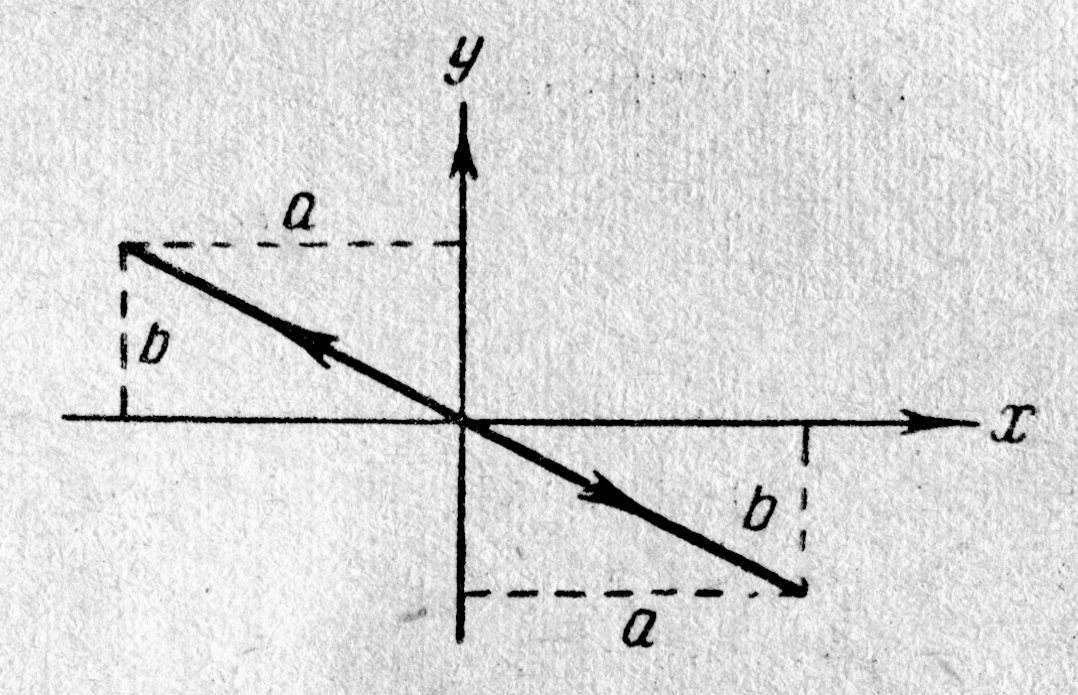

Рис. 5.5. Сложение взаимно перпендикулярных колебаний a = ± p

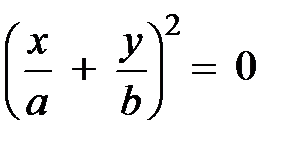Разность фаз складываемых колебаний a = ± p. Уравнение (5.11) принимает вид , откуда следует, результирующее движение представляет собой гармоническое колебание вдоль прямой (рис. 5.5):

.

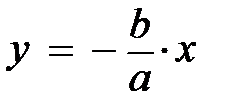Здесь для настойчивого студента заметим, сказанное нужно проверить, подставляя в написанное уравнение эллипса (5.11) значения или , что позволит осознать – куда движется точка в момент времени t = 0, вверх или вниз. Такого рода предложение относится и к рис. 5.4.

Разность фаз складываемых колебаний a = ± p/2. Уравнение (5.11) принимает вид:

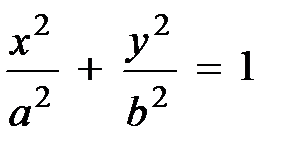, (5.13)

т. е. приходим к уравнению эллипса, приведённого к координатным осям, а полуоси эллипса равны соответствующим амплитудам колебаний. К тому же результату приходим, если воспользоваться уравнениями (5.10). Действительно, если учесть разность фаз, уравнения (5.10) принимают вид:

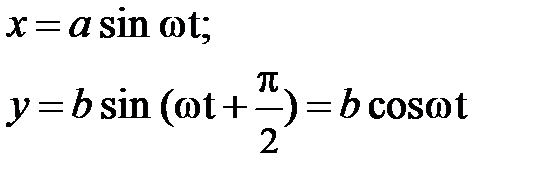. (5.13а)

Выразив функцию sin wt и cos wt через соответствующие координатным осям смещение и амплитуду, приходим к уравнению эллипса ; т. е. в результате сложения таких колебаний точка в плоскости ХУ описывает эллипс (рис. 5.6). Если a = b, эллипс вырождается в окружность.

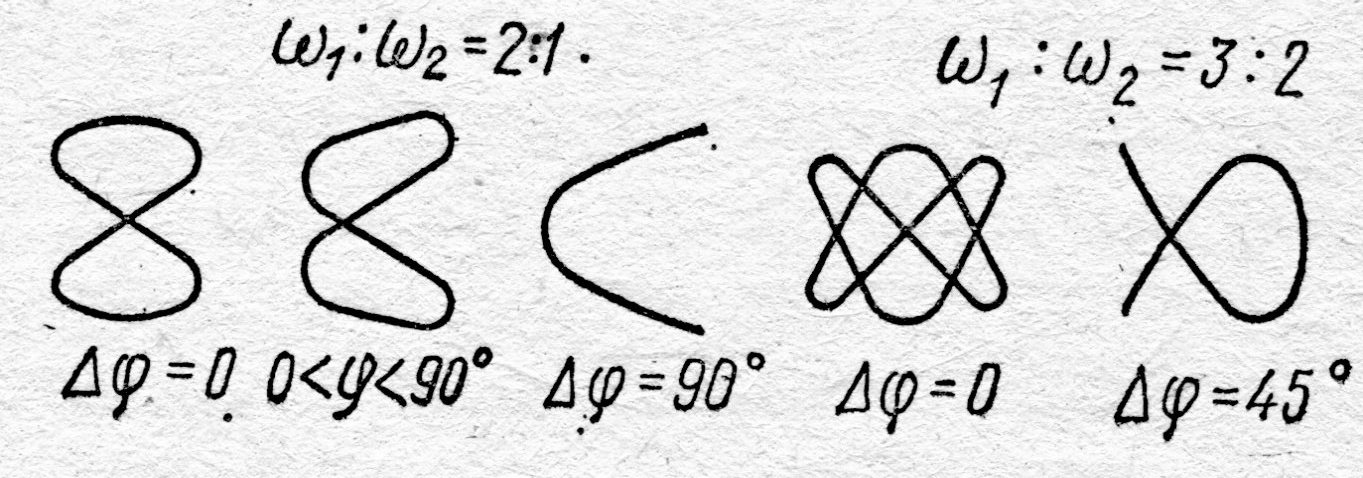
Рис. 5.7. Сложение колебаний разных частот

Рис. 5.6. Сложение взаимно перпендикулярных колебаний a = p/2

Между разностями фаз + p/2 и – p/2 есть различие, несмотря на то, что они и дают тождественные траектории. В одном случае луч обегает эллипс (окружность) по часовой стрелке, а в другом – против. Чтобы убедиться в этом, вернёмся к исходным уравнениям (5.13а). Если t = 0, из (5.13а) немедленно следует: х = 0, у = b, тело (частица) находится в точке В (рис. 5.6). При возрастании времени из (5.13а) следует, координата х увеличивается, тогда как координата у уменьшается (рис. 5.13а); частица движется из точки В в точку А, по часовой стрелке. Обратное движение настойчивый студент может проанализировать самостоятельно, если запишет пару уравнений (5.13а) с учётом начальной фазы a = –p/2.

Если частоты различаются, что вполне эквивалентно случаю непрерывно меняющейся разности фаз, то в результате сложения колебаний траектория результирующего движения образует сложные кривые, форма которых определяется не только отношением частот складываемых колебаний, но и их амплитудами. Примеры этих причудливых кривых, называемых фигурами Лиссажу, показаны на рис. 5.7.

В заключение заметим, из сказанного ранее в [3, с. 29–34] и в этом параграфе следует, в изотропном поле упругих сил не только равномерное движение по окружности можно представить как совокупность независимых гармонических колебаний вдоль осей Х и У. Наоборот, в таком поле гармонические колебания вдоль любой прямой и вообще движение по эллипсу можно представить как совокупность независимых равномерных движений, происходящих по окружностям (либо одинакового, либо различных радиусов) по часовой или против часовой стрелки. Указанные свойства движения частиц найдут в дальнейшем (часть 3) отражение в явлениях поляризации электромагнитных волн и не только.