Вынужденные колебания

До сих пор мы рассматривали колебания в системе, предоставленной самой себе. Независимо от характера возбуждения колебания определялись лишь параметрами самой системы. В частности, колебания тронутой струны имеют одну и ту же частоту вне зависимости от того, щипком или ударом её заставили звучать.

В то же время имеется ряд способов, при помощи которых телу можно «навязать» колебания с внешней частотой. Такие вынужденные колебания можно осуществить, если создать связь между двумя телами, способными колебаться. Одно из них будет вынуждать колебаться другое. Например, неточно уравновешенный мотор совершает колебания, которые передаются фундаменту; фундамент будет совершать колебания. На рис. 5.9 показано устройство, при помощи которого можно (вращением эксцентрика) привести маятник в состояние вынужденных колебаний. Во всех этих случаях на тело действует периодическая сила, меняющаяся с некоторой частотой w; такую силу уместно назвать внешней.

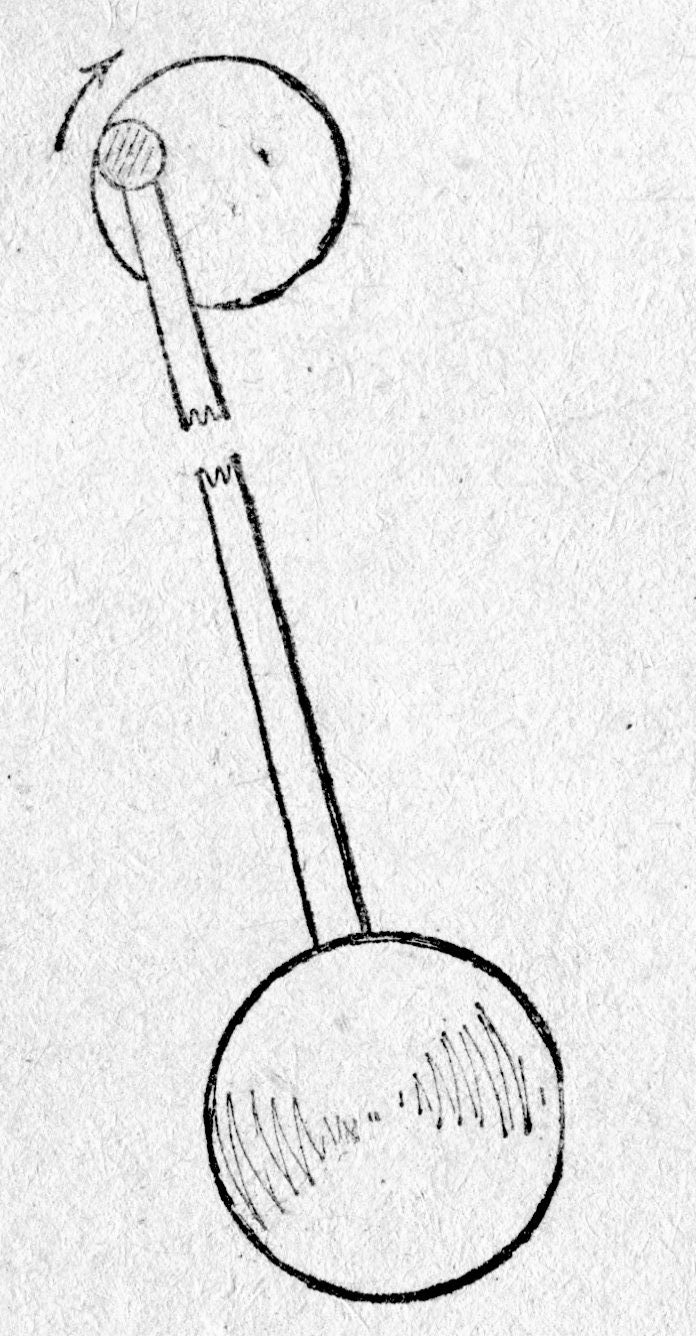
Рис. 5.9. Возникновение вынужденных колебаний

Вынужденные колебания устанавливаются не сразу. Должно пройти некоторое время, пока связанное с колебательной системой тело само придёт в колебание. В конце концов, установится какая-то амплитуда вынужденных колебаний, а частота колебаний будет точно равна w; частоте внешней периодической силы (не напоминает ли вам это качели?!).

Перейдём к аналитическому рассмотрению вынужденных колебаний. Пусть вынуждающая сила изменяется со временем по гармоническому закону с частотой w:

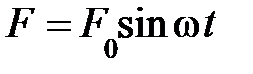. (5.33)

Составляя уравнение движения, следует учесть квазиупругую силу, силу сопротивления среды и вынуждающую силу (5.33). По-прежнему будем считать силу сопротивления пропорциональной скорости, что соответствует достаточно малым колебаниям. Тогда уравнение движения примет вид:

.

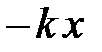
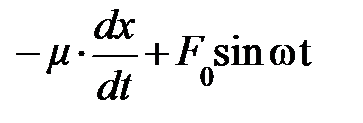Разделим это уравнение на массу m, примем к вниманию, что 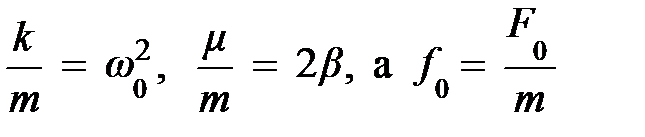и, перенеся квазиупругую силу и силу сопротивления в левую часть, получим неоднородное линейное дифференциальное уравнение второго порядка:

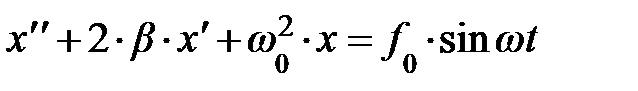, (5.34)

здесь учтено, что dx / dt º , а d ² x / dt ² º . Описываемые уравнением (5.34) колебания называются вынужденными колебаниями. Пусть в результате установления колебаний под действием внешней силы они происходят по закону:

х = a sin (w×t + j), (5.35)

где a – амплитуда колебаний; w – частота установившихся колебаний, равная частоте вешней периодической силы; j – сдвиг фазы между установившимися колебаниями и вынуждающей силой (5.33), обусловившей эти колебания. Неизвестные параметры – амплитуда установившихся вынужденных колебаний а, разность фаз j между колебаниями внешней силы и смещения х (t) – должны выражаться через параметры системы w ₀, F ₀, w и b. Вычисление этих параметров несколько громоздко и мы ограничимся рассмотрением лишь установившихся колебаний.

Если решением уравнения (5.34) является уравнение (5.35), найдём его первую и вторую производные 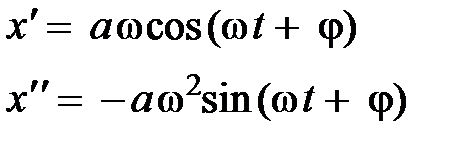и, подставив их в уравнение (5.34), приходим к выражению:

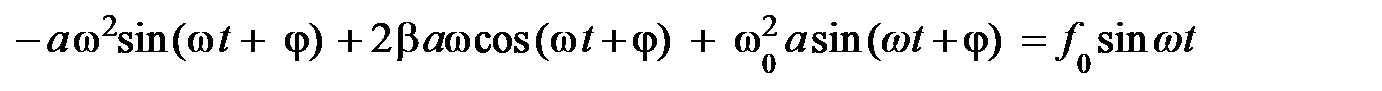. Воспользовавшись тригонометрическим тождеством (5.2), уравнение (5.34) преобразуем к виду:

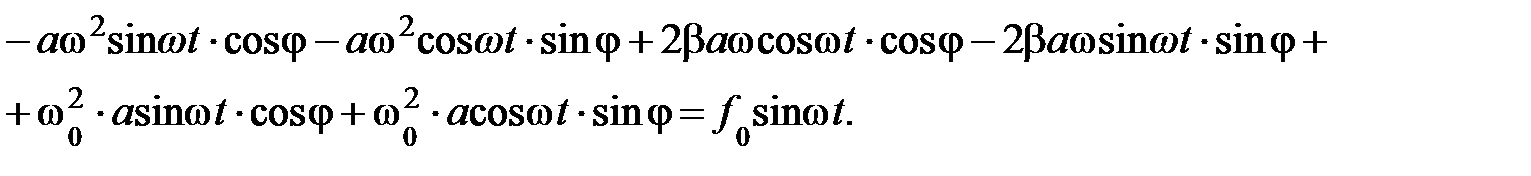
Что даёт нам последнее преобразование? Тригонометрическую функцию от суммы аргументов нам удалось преобразовать в произведение тригонометрических функций отдельных аргументов, что позволяет группировать члены, содержащие cos wt и sin wt. Отсюда немедленно получаем:

Поскольку полученное равенство должно выполняться для любого момента времени, мы должны потребовать, чтобы коэффициенты слева и справа при cos wt и sin wt были равны. Таким образом, получаем два уравнения, позволяющие определить сдвиг фазы j и амплитуду колебаний а:

(5.36а)

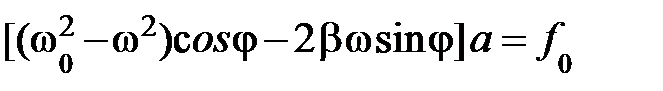. (5.36б)

Действительно, как следует из уравнения (5.36а), сдвиг фазы:

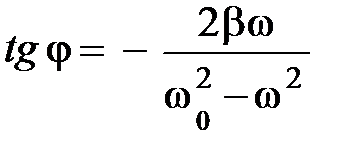. (5.37)

Для нахождения амплитуды установившихся колебаний возведём в квадрат уравнения (5.36 а) и (5.36 б) и сложим их:

.

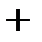
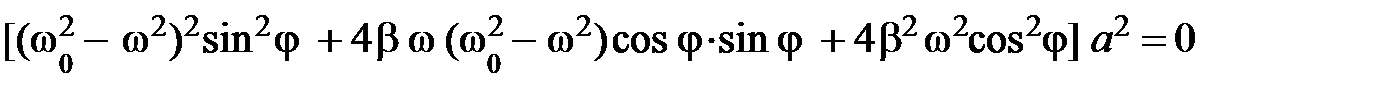
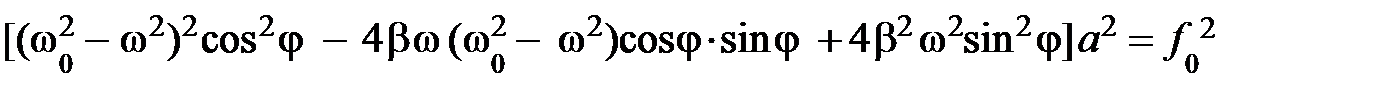Результатом сложения является уравнение:

,

откуда следует, что амплитуда вынужденных колебаний:

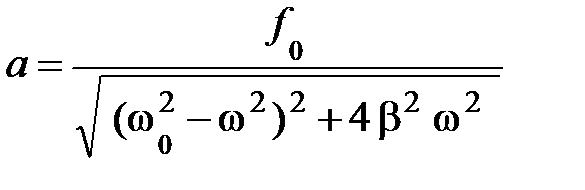. (5.38)

Таким образом, если на тело действует сила, изменяющаяся по гармоническому закону с частотой w, то тело колеблется с той же частотой. При этом амплитуда вынужденных колебаний зависит от амплитуды и частоты внешней силы, от параметров колебательной системы и коэффициента затухания b. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приведена на рис. 5.10. Резонансные кривые, приведён-ные на рис. 5.10, соответствуют различным значениям параметра b, см. (5.23); чем меньше b, тем выше максимум кривой.

При стремлении частоты вынуждающей силы w к нулю кривые приходят к одному и тому же предельному значению смещения х = а = f ₀/ w ₀ ² = F ₀/ k. Пытливый читатель, осуществляя проверку (5.38), найдёт предложенные обозначения символов на с. 79.

Рис.5.10. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы

В заключение данного параграфа остановимся на анализе особенностей резонанса. Для его полного анализа в работе [2] предлагается учесть механизм потерь энергии в системе за счёт сопротивления среды. Чтобы амплитуда колебаний в резонансе достигла максимума («не уходила» в бесконечность), необходима синхронность в изменении вынуждающей силы F _вн. (t) = F ₀ sin w t и проекций скорости частицы (тела) u_х (t). С этим следует согласиться, поскольку для обеспечения максимальной эффективности воздействия внешняя сила должна всегда действовать в направлении скорости и изменять знак вместе со скоростью. Такая синхронность достигается, если j в (5.35) равно p/2, ибо тогда:

х _рез.(t) = | а _рез |×sin(w _рез.× t – p/2) = | а _рез |×cos(w _рез.× t),

а (5.39)

u_х (t) = х _рез. (t) ^/ = w _рез.×| а _рез |×sin(w _рез.× t).

Аналитические выражения (5.39) для координаты и проекции скорости частицы (тела) в области резонанса w _рез.» w ₀ позволили А.Д. Суханову [2] найти резонансную амплитуду | а _рез | обходным путём: с учётом затухания, и не имея полного выражения для | а |. Для этого пришлось принять во внимание тот факт, что для достижения максимального значения амплитуды вынужденных колебаний в области резонанса необходима полная компенсация: мощности внешней силы | W _вн(t)|, получаемой системой, и мощности | W _сопр.(t)|, теряемой вследствие сопротивления среды. Иными словами, мы можем потребовать, чтобы

| F _вн. (t)×u_х (t)| = F ₀sin(w _рез. t)×u_х (t) = m×f ₀×sin(w _рез. t)× w _рез.| а _рез |sin(w _рез. t) =

= F _сопр. (t)×u_х (t)| = m u_х (t)×u_х (t) = 2 b mw _рез.²×| а _рез |²×sin²(w _рез.× t).

Из равенства третьей и шестой записи следует f ₀ = 2 b w _рез.×| а _рез | и тогда:

| а _рез | . (5.40)

Резонансную амплитуду вынужденных колебаний можно найти из выражения (5.38). Для этого придётся воспользоваться математическим методом исследования функций. Проверьте! Должно получиться с точностью до постоянной b. Предложенный выше метод несколько глубже, хотя бы потому, что основан на законах сохранения энергии в физических системах.