Затухающие колебания

С динамикой некоторых простейших колебательных движений в стационарных состояниях мы уже встречались в работе [3, с. 29–34]. Сейчас проведём их более последовательный анализ на основе уравнений движения Ньютона-Эйнштейна, что позволит обобщить их на колебательные движения в произвольных нестационарных состояниях. Для простоты рассуждений ограничимся нерелятивистским приближением (u << с) и учтём, приводящая к колебаниям упругая сила и аналогичные ей воздействия сами зависят от координат; в частности, например, F _у = – kx = F (x).

Рассмотрение примеров колебательных движений под действием произвольно ориентированной упругой силы F = – kx показало, что его всегда можно представить как совокупность одномерных колебательных движений. Поэтому основное внимание будем уделять одномерным задачам. Но прежде уделим внимание уравнениям движения Ньютона-Эйнштейна.

В рассуждениях, проведённых выше в модели несвободной частицы, фундаментальные характеристики её состояния – импульс, полная энергия и момент импульса – по-прежнему имеют смысл. Однако теперь все эти величины (характеристики), как правило, не сохраняются, а потому характер движения свободной и несвободной частицы, совершенно различен. Приступая к анализу движения несвободной частицы, необходимо их как-то классифицировать, выделив наиболее близкие к движению свободной частицы. В качестве характеристики состояния частицы желательно выбрать величину, обладающую рядом универсальных свойств. И для этого пригодна механическая энергия частицы Е _мех = Е _мех(). Действительно, будучи зависимой от характеристик состояния частицы механическая энергия является характеристикой её состояния. В то же время как характеристика состояния она обладает рядом преимуществ. В частности, сохраняется даже при наличии внешнего воздействия; одинаково пригодна для свободной и несвободной частиц; может быть обобщена на более сложные физические системы. Состояния частицы, в которых имеет смысл и сохраняется механическая энергия Е _мех = const, принято называть стационарными, все остальные – нестационарными. Однако заметим, если движение частицы будет не одномерным, то величина Е _мех уже не может быть единственным параметром её состояния.

Итак, нас интересуют уравнения, управляющие изменением характеристик частиц в произвольных нестационарных состояниях. Не в последнюю очередь это обусловлено тем, что встречающиеся в природе внешние воздействия довольно часто соответствуют непотенциальным силам.

Как следует из опыта, при движении частицы под действием потенциальных сил справедлив закон сохранения механической энергии Е _мех = = const, или, как следует из (2.11),

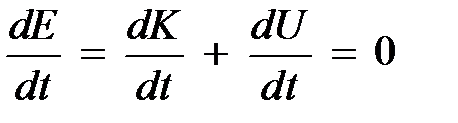. (5.14)

Уравнению (5.14) можно придать вид:

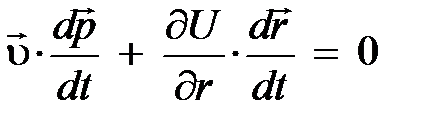, (5.15)

если учесть, что , а также может быть представлено как ; эти преобразования следуют из обобщений гл. 2. В преобразовании кинетической энергии через потенциальную энергию U для нас важны последние два равенства, влияющие на вид уравнения (5.14) и преобразующие его в уравнение (5.15). Полученное уравнение (5.15) объединяет два независимых утверждения. Во-первых, в модели несвободной частицы в любой момент времени справедлива та же связь между скоростью u(t) º º dr / dt и импульсом p (t), что и в модели свободной частицы; скорость определяется импульсом частицы (нерелятивистское приближение):

. (5.16)

Во-вторых, если учесть, что и привлечь его, как и уравнение (5.16), для преобразования формулы (5.15), то последняя принимает вид 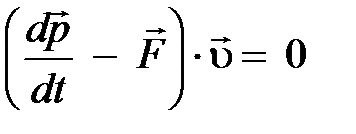. Естественно, полученное равенство будет иметь место при произвольном значении скорости, если выполняется уравнение:

. (5.17)

Другими словами, исходные характеристики состояния частицы { } обеспечивают выполнение закона сохранения механической энергии (5.14) и, следовательно, движение частицы в стационарных состояниях, если они подчиняются уравнениям (5.16) и (5.17), где выражения u(р) и F (r) в правых частях считаются известными из опыта независимо. Это значит, при рассмотрении движения в стационарных состояниях характеристиками состояния частицы не только можно, а иногда и целесообразно выбирать не сохраняющиеся во времени величины . При этом окончательные выражения для законов движения частицы в стационарных состояниях от этого, разумеется, не зависят.

Что же изменится, если мы перейдём в описании движения частицы от потенциальных сил к непотенциальным? Прежде всего, уравнение (5.16) останется неизменным, поскольку оно определяется только моделью несвободной частицы. Уравнение (5.14) и следующее из него уравнение (5.17) в этом случае не выполняются. Заметим также, модифицировать уравнение (5.14) невозможно, поскольку оно справедливо только для потенциальных сил. Вместе с тем, если отказаться от слишком тесной связи [2; 6] уравнений (5.14) и (5.17) и считать уравнение (5.17) независимым, то его можно обобщить и на случай непотенциальных сил [2].

Тогда, как считает А.Д. Суханов, следуя Ньютону, можно предположить, что уравнение (5.17) имеет место не только для потенциальных сил, но и для любых непотенциальных сил:

. (5.18)

Это соотношение называют вторым законом Ньютона и в такой форме оно применимо при любых скоростях и любых внешних воздействиях на частицу. При малых скоростях (u << с), когда 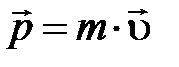, второй закон Ньютона записывают в виде, известном ещё из курса средней школы:

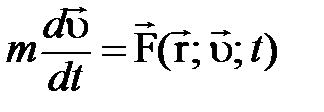, (5.19)

где – вектору ускорения.

Необходимо заметить, второй закон Ньютона представляет собой один из законов изменения со временем характеристик состояния материального объекта, к которому применима модель несвободной частицы. Таким образом, задача нахождения закона движения частицы, осуществляющей затухающие колебания, сводится к решению системы взаимосвязанных дифференциальных уравнений для характеристик состояния частицы:

;

.

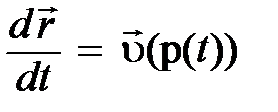Эту систему уравнений принято называть уравнениями Ньютона - Эйнштейна. Заслуга Эйнштейна здесь состояла в том, что он подтвердил указанную роль импульса при u ® с и нашёл взаимосвязь 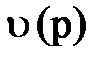, справедливую при любых скоростях [2]; см. (4.25).

Таким образом, приступая к поиску уравнения движения затухающих колебаний необходимо решить систему уравнений (5.20). Вместе с тем, как утверждают физики-теоретики [2], в нерелятивистском приближении (u << с) часто бывает целесообразно перейти от системы уравнений первого порядка (5.20) к одному дифференциальному уравнению второго порядка, подставив (5.16) в левую часть (5.19). В результате получим уравнение движения Ньютона, содержащее производные второго порядка:

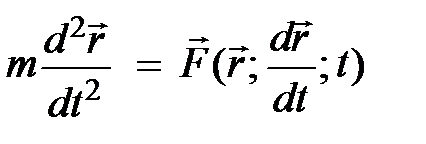. (5.21)

Рис. 5.8. Колебательная система с одной степенью свободы

Приобретя уравнение движения, перейдём к анализу колебательного движения в произвольных нестационарных состояниях (закон сохранения энергии не работает). Рассмотрим колебательную систему с одной степенью свободы (рис. 5.8), в которой колебания происходят вдоль оси х. Уравнение движения Ньютона (5.21) для координаты Х принимает вид:

. (5.22)

Здесь в проекцию результирующей силы дают вклад сила упругости , обеспечивающая растяжение и сжатие, и сила сопротивления среды, пропорциональная скорости движения тела ; знак «–» указывает на то, что направление силы всегда противоположно направлению смещения или скорости движения. Другими внешними силами пренебрежём. Ограничимся малыми отклонениями от положения равновесия. С учётом этих приближений уравнение движения (5.22) с начальными условиями { } примет вид:

.

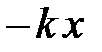
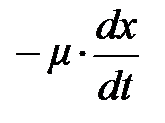Разделим это уравнение на массу тела m и, вводя обозначения,

, (5.23)

приходим к дифференциальному уравнению вида:

. (5.24)

Описываемые уравнением (5.24) колебания называются собственными затухающими колебаниями. Здесь w₀ представляет собой ту частоту, с которой совершались бы колебания системы при отсутствии сопротивления среды, т. е. m = 0. Её принято называть собственной частотой колебательной системы. Подобного рода процессы, движение, совершаемое телом или частицей около положения равновесия, часто встречаются в природе. Покачивается ветка дерева, дрожит пружинка, колеблется атом, входящий в кристаллическую решётку.

Наличие сопротивления среды приводит к тому, что амплитуда колебаний с течением времени уменьшается. Поэтому уравнение (5.24) удовлетворяется решением вида (5.6), если амплитуда колебания уменьшается со временем, т. е.

х = А (t) sin (w×t + j₀). (5.25)

Здесь x º x (t) – смещение системы от положения равновесия в любой момент времени движения; А (t) – некоторая функция, отражающая зависимость амплитуды колебания системы от времени; w – частота колебаний системы при наличии сопротивления среды; j₀ – начальная фаза колебаний. Таким образом, решая уравнение (5.24) необходимо найти закон изменения амплитуды колебания со временем и частоту колебаний w.

Если уравнение (5.25) является решением дифференциального уравнения второго порядка (5.24), продифференцируем (5.25) по t и найдём первую dx / dt º и вторую d ² x / dt ² º производные:

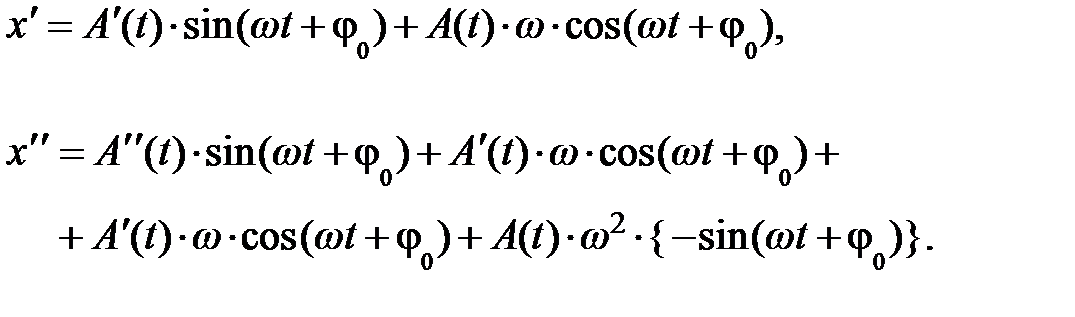
Собрав однородные члены, приходим к уравнениям вида:

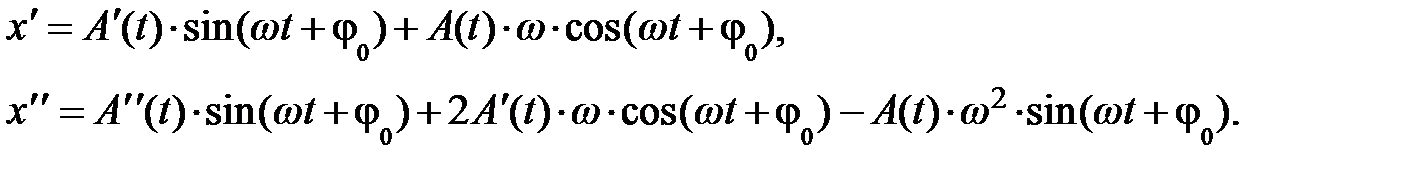
После подстановки этих производных в уравнение (5.24), приходим к несколько громоздкому, но подающему надежду на решение уравнению:

Упростим полученное выражение, в частности, заменим 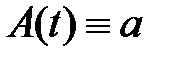, не забывая, что а является функцией времени, и сгруппируем члены при функциях sin и cos. В результате преобразований приходим к уравнению:

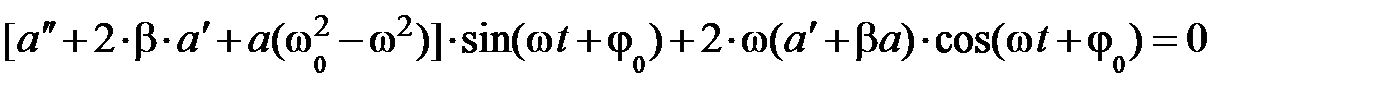. (5.26)

Равенство нулю уравнения (5.26) при любых значениях времени t возможно, если константы в его левой части при функциях sin (w×t + j₀) и cos (w×t + j₀) будут равны нулю. Из этого условия следуют два уравнения:

Поскольку a ^/ º da / dt, уравнение (5.28) можно представить в виде:

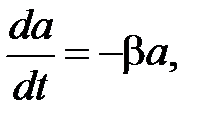разделяя переменные, приходим к выражению

Интегрирование последнего равенства ведёт к выражению , подставляя в это выражение верхний и нижний пределы, приходим к уравнению 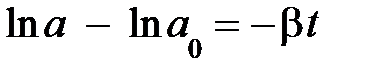; если учесть, что разность логарифмов равна логарифму частного, то 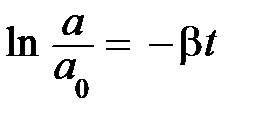. Наконец, проведя операцию потенцирования, получаем уравнение амплитуды:

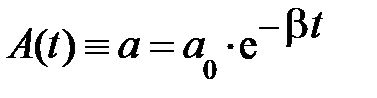. (5.29)

Отсюда следует, при не слишком большом затухании колебания описываются уравнением:

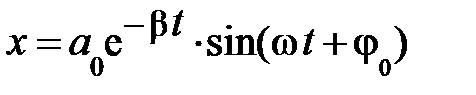. (5.30)

Если пытливый читатель возьмёт первую и вторую производные от уравнения (5.29) и подставит их в выражение (5.27), то немедленно придёт к взаимосвязи частот w и w ₀: w ² = w ²₀ – b ²; отсюда следует, при наличии слабой силы сопротивления среды b ² << w ²₀ колебания осуществляются с частотой w» w ₀.

Для характеристики такого рода колебательных систем вводится понятие добротности колебательной системы. Она характеризует быстроту уменьшения амплитуды колебаний в системе и вычисляется по формуле:

. (5.31)

Здесь l – логарифм от декремента затухания, а декремент затухания в свою очередь представляет собой отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, и имеет вид:

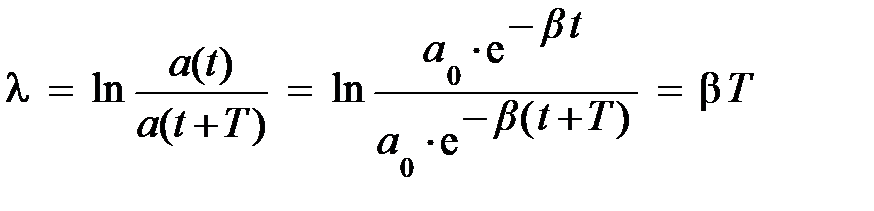, (5.32)

где b и Т определяются из уравнения (5.23).

Таким образом, добротность Q, как и логарифмический декремент затухания l, служит удобной характеристикой отношения характерных временных промежутков двух динамических процессов, одновременно происходящих в колебательной системе при наличии затухания. Некоторую витиеватость последней фразы в той её части, что касается «двух динамических процессов», можно снять следующими преобразованиями. Из уравнения (5.29) с учётом (5.32) следует 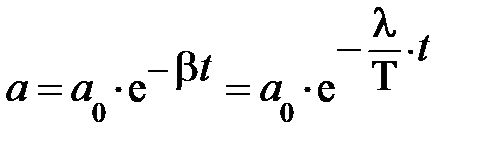. Если за время t = t амплитуда колебаний уменьшается в e – раз (основание натурального логарифма), то уравнение (5.29) примет вид: . Из последней записи немедленно следует 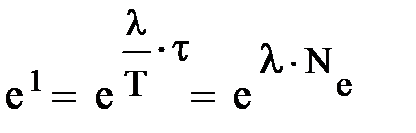. Последнее равенство имеет право на существование, если показатели степени слева и справа равны и тогда (преобразование желательно проделать); здесь и в (5.31) 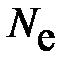– число колебаний, за которое амплитуда уменьшается в e – раз (e–основание натурального логарифма); и тогда действительно , а Т и t являются параметрами двух динамических процессов – возможных колебаний в системе и потери её энергии. Именно поэтому все встречающиеся в природе колебания при отсутствии внешних воздействий оказываются затухающими.