Плотность энергии в бегущей упругой волне

В предыдущих параграфах данной главы мы убедились в том, что малые деформации элемента сплошной среды приводят к возникновению упругих волн. Упругие волны в сплошной среде – это согласованное «коллективное» движение системы «частиц» – элементов среды. Каждый элемент среды испытывает смещение u (х, t), определяемое местом его расположения (пространственная форма волны) и временем. Изменения величины u (х, t) и связанных с ней физических характеристик распространяются с течением времени с фазовой скоростью u_ф. Чтобы убедиться в качественном своеобразии упругих волн как «коллективном» типе движения системы частиц, рассмотрим вопрос об энергии бегущих упругих волн. Наблюдаемое сходство упругих волн в разных сплошных средах позволяет, для простоты рассуждений, обратиться к продольным упругим волнам. При этом мы можем ссылаться на упругие волны в цепочке атомов и в сплошном твёрдом теле (раздел 6.1).

Вспомним, внутренняя энергия цепочки атомов при тепловом движении может быть представлена как сумма кинетической и потенциальной энергий (энергия, не зависящая от температуры, не учитывалась) вида:

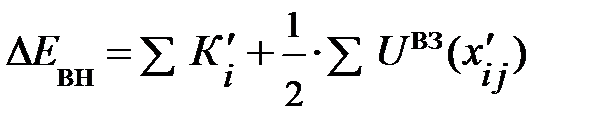; (6.8)

здесь К ^/ _i – кинетическая энергия i -того элемента цепочки, 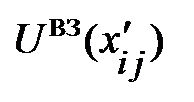– потенциальная энергия взаимодействия i,j – элементов; множитель 1/2 компенсирует наличие одинаковых вкладов = .

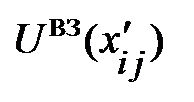хi хj +D uj (t)

Рис. 6.6. Смещение элементов среды, лежащих на одной прямой, вдоль которой распространяется продольная волна.

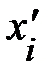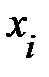В обозначенном нами случае = + u_i (t), где 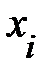– положение i- го элемента среды в состоянии равновесия, а u_i (t) – смещение, вызванное упругой деформацией, распространяющейся в среде (рис. 6.6). В этом пытливый читатель так же может убедиться, обратившись к рис. 6.2.

И тогда кинетическая энергия i – того элемента среды

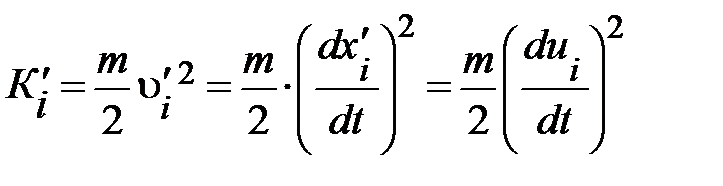; (6.9)

убедиться в справедливости аналитической записи можно через рис. 6.6.

Потенциальная энергия взаимодействия, с. 81, запишется:

;

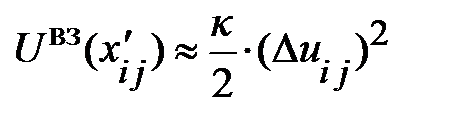где 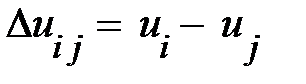, в этом настойчивый читатель может убедиться, обратившись к рис. 6.6; как и при записи кинетической энергии, не будем учитывать постоянную энергию в состоянии равновесия.

В итоге, внутренняя энергия цепочки элементов сплошной среды может быть выражена только через смещение элементов среды. Действительно, внутренняя энергия i -го элемента (атома)

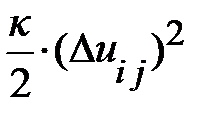+ . (6.10)

В непрерывном приближении для цепочки элементов среды длиной D L, содержащей D N атомов (элементов), расстояние между которыми a, а длина цепочки D L = D N × a, внутренняя энергия D E содержит D N одинаковых слагаемых (6.10). Тогда для внутренней энергии этого элемента цепочки из D N атомов, заменив операцию суммирования в (6.8) умножением, получим

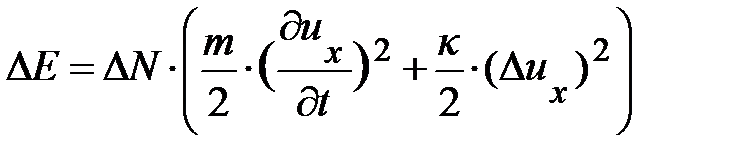. (6.11)

Заменим теперь через плотность r _о и объём D V массу D М = D N × m = = r _о×D V, а коэффициент упругости k через модуль Юнга c – хи, k = = c ×D S / а. Пытливый читатель в этом может убедиться, если обратится к рис. 6.6 и воспользуется законом Гука. (F = k ×D u, F = c ×D S ×e, e = D u/а; здесь a – расстояние между ближайшими атомами среды (упругие свойства не зависят от длины образца); D u – деформация между ближайшими атомами, возникшая в результате внешнего воздействия, и << а; D S – площадь поперечного сечения цепочки атомов, e – относительное увеличение расстояния между ближайшими атомами.)

Теперь уточним разность смещений между двумя соседними атомами. Если воспользоваться разложением функции в ряд Тейлора, то .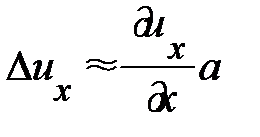

Убедимся в правоте утверждения из рассуждений. Пусть смещение частицы I сплошной среды между точками 1-3 (рис. 6.6) отражается функцией u (t, х), а между частицами 2-4 функцией u (t, х +D u_j (t, x)); здесь D u_j (t, x) – смещение j -го атома в результате распространения упругой деформации. Смещение частицы под номером 3 в состояние 4 запишется: D u _j(t, x)=D u_i + u (t, x +D u _j(t, x))– u (t, х); здесь D u_i – смещение i -того атома из состояния 1 в 2. Тогда изменение D u _x=D u_j –D u_i запишется: D u _x= u (t, х +D u_j)– u (t, х). Теперь вспомним, частная производная от функции u ^/ (t, х) = = 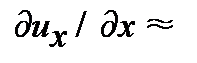[ u (t, х +D u_j) – u (t, х)] / D x = D u_x /D x. Отсюда немедленно следует, что 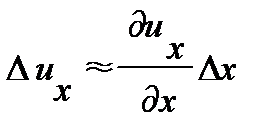. В нашем случае D х = а, расстоянию между атомами.

Введённые физические характеристики среды и характеристики смещения её частиц при возникновении упругой деформации позволяют преобразовать уравнение (6.11) для внутренней энергии элемента цепочки из D N атомов длины D L = D N × a к виду:

,

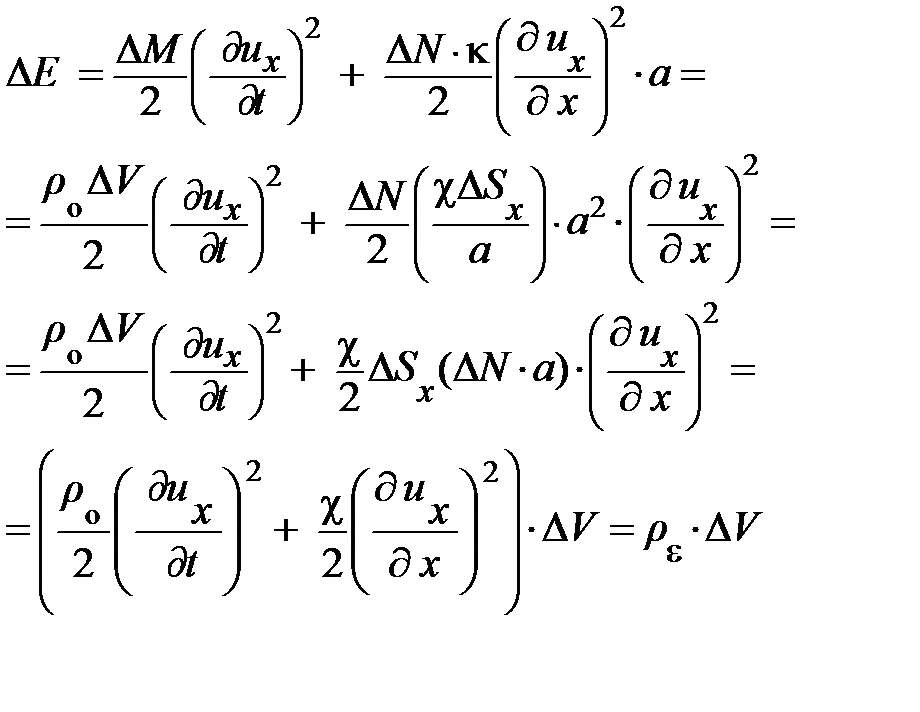здесь D V = D S_х ×(D N × а) = D S_х ×D L, где D L – длина элемента цепочки.

Величина

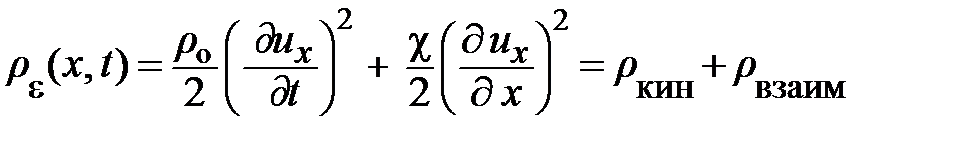, (6.12)

называется плотностью внутренней энергии цепочки атомов в приближении сплошной среды; где r _кин – плотность кинетической энергии, а r _взаим. – плотность энергии взаимодействия.

Теперь вспомним, для бегущей вдоль оси х упругой волны справедливо соотношение:

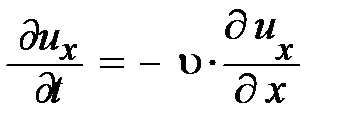. (6.13)

В этом пытливый читатель может убедиться, если найдёт первую производную от функции упругой деформации , распространяющейся в сплошной среде, по переменной x и t (см. 6.4 а, 6.5 а).

Из уравнений (6.12) и (6.13) следует

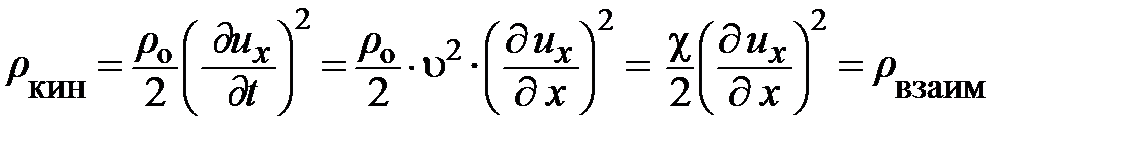; а 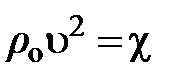. (6.14)

Иначе говоря, в любой момент времени и в любой точке пространства плотность кинетической энергии в сплошной среде равна плотности энергии взаимодействия. Отсюда следует, плотность энергии в упругой волне равна:

. (6.15)

При прохождении бегущей упругой волны вдоль оси х происходит распространение энергии. Процесс переноса энергии характеризуется вектором плотности потока энергии j_x, модуль которого равен количеству энергии переносимой в единицу времени через единичную (например, 1 м²) поперечную площадку. Таким образом, упорядоченный перенос энергии j_x вдоль оси х должен иметь форму произведения плотности энергии 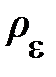на вектор скорости смещения элемента объёма .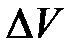

Чтобы записать это произведение, уточним механизм упорядоченного переноса энергии в сплошной среде. Из работы [2] следует, в сплошной среде возможны два механизма упорядоченного переноса энергии через какую-либо поверхность. Одним из них является перенос плотности энергии вида (6.12) со скоростью смещения элемента среды D V. Эта доля энергии жёстко связана с каждым элементом среды как с «частицей» и переносится при движении частицы точно так же, как переносится масса и другие характеристики.

Однако возможен упорядоченный перенос энергии и через поверхность D S_х, окружающую элемент среды объёмом D V. Действительно, на границе объёма возникают упругие напряжения (рис. 6.7): 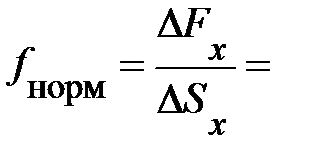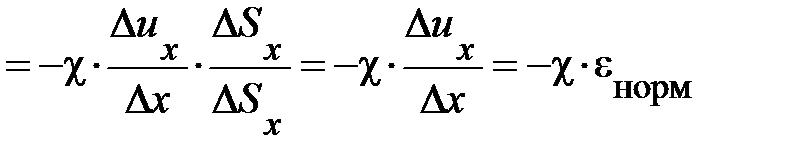; где D F _х – сила, которую необходимо приложить, чтобы удлинить стержень длины D х на величину D u_х << D х; c–хи – модуль упругости твёрдого тела. При деформации элемента среды упругие напряжения производят работу, уменьшая или увеличивая внутреннюю энергию, заключённую в этом элементе среды (рис. 6.7.). И тогда работу нормального упругого напряжения в единицу времени (мощность) можно записать 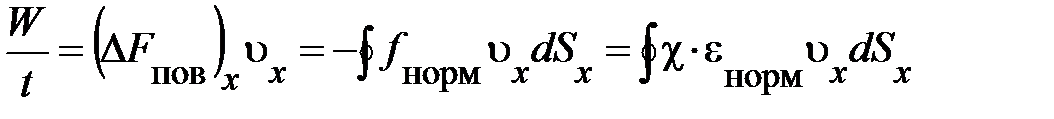. Тем самым, выражение для мощности даёт в плотность потока энергии через поверхность, окружающую элемент сплошной среды, вклад вида D r_e ×u _х; здесь D r_e ×u _х =c×e_норм – плотность энергии внешнего упругого воздействия на элемент среды D V.

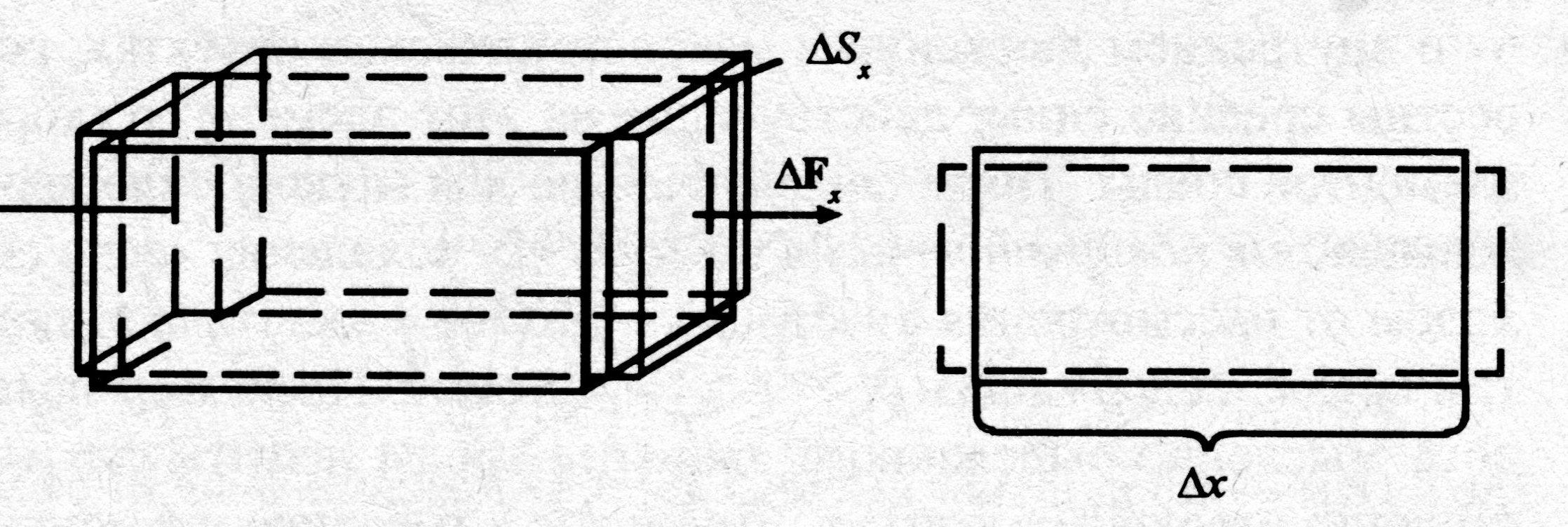
Рис. 6.7. Линейное растяжение твёрдого тела однородными силами ± DFx, действующими в обе стороны вдоль его оси х

Таким образом, поток механической энергии элемента среды D V, но уже вместе с его окружением, т. е. поток энергии расширенной замкнутой системы (рис. 6.7), может быть записан:

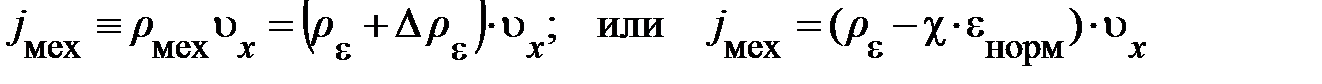(6.16)

Учтём теперь то, что мы рассматриваем лишь малые смещения элемента сплошного твёрдого тела. Тогда из (6.15) 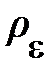пропорционально 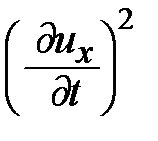, а величина , с учётом (6.13) пропорционально 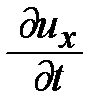, так что при малых смещениях сплошного твёрдого тела r_e << D r_e. Таким образом, в этом приближении вектор плотности потока механической энергии в бегущей волне, равный:

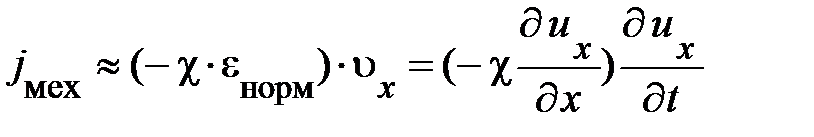, (6.17)

определяется лишь вкладом работы упругих поверхностных сил.

Это приближённое выражение может быть представлено в другом виде, если учесть (6.13) и (6.14), из которого следует, что . Проделав преобразования, пытливый читатель приходит к выражению вида:

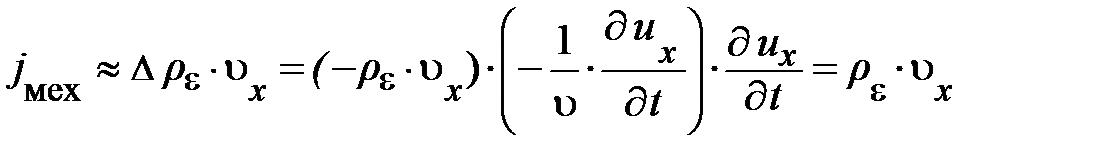. (6.18)

Другими словами, в указанном приближении упругая волна описывает перенос плотности механической энергии, либо перенос плотности внутренней энергии также в направлении оси х, но при этом r_e << D r_e. Выражение (6.18) для потока механической энергии в бегущей волне справедливо и для поперечных упругих волн в твёрдом теле и для упругих волн в жидкости. Убедиться в этом можно в работе [2, глава 4].

В заключение параграфа заметим. Упругие волны – это такой тип «коллективного» движения сплошной среды и, следовательно, такой способ распространения энергии в пространстве и во времени, при котором с фазовой скоростью внутренняя энергия может переноситься на любые расстояния практически без переноса массы. При этом энергия покоя, равная произведению плотности массы на скорость света в квадрате, много больше плотности энергии 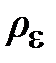. Тем самым предполагается, что «частицы» или элементы среды остаются вблизи их равновесных положений.

Таким образом, бегущая упругая волна как самостоятельный тип движения сплошной среды принципиально отличается от способа переноса энергии при движении одиночной частицы, когда одновременно переносится как масса частицы, так и вся связанная с ней энергия. По сути, вместо детального рассмотрения движения элемента сплошной среды объёма 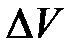, играющего, по существу, роль новой «квазичастицы» индивидуального типа, мы перешли к рассмотрению качественно новых объектов – бегущих волн, характеризующих уже движение сплошной среды в целом. В простейшем случае эти волны напоминают нормальные моды (колебания) цепочки атомов, о которых упоминалось в параграфе (6.1).

Нормальную моду (распространяющееся колебание) с гармонической зависимостью от времени как простейший вариант модели бегущей волны, можно сопоставить с частицей, движущейся в стационарном состоянии как простейшим вариантом модели частицы. У частицы в этом случае сохраняется механическая энергия Е _мех = const, тогда как у бегущей нормальной моды гармонического типа сохраняется средний поток механической энергии 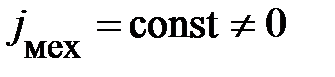. Подобное соответствие качественно разных моделей должно сыграть особо важную роль при поиске единого подхода к описанию природы в квантовой физике.