Сложение однонаправленных колебаний

В предыдущих главах на простых примерах мы ознакомились с общими методами нахождения законов движения частиц в стационарных состояниях. Применим их к более сложным задачам, приводящим к возникновению различных колебательных движений. Характерная особенность таких движений – наличие периодического процесса, обеспечивающего ограниченное движение частицы вблизи её положения равновесия. Закономерности колебательных движений интересны не только сами по себе. В дальнейшем они найдут приложения во многих разделах физики, в которых приходится иметь дело с малыми отклонениями произвольной физической системы от её равновесного состояния. С некоторыми простейшими примерами колебательных движений в стационарных состояниях мы уже встречались в работе [3, с. 29–34], а сейчас проведём анализ движения частицы, участвующей одновременно в двух колебательных процессах одного направления. Такую ситуацию можно «поймать», подвесив шарик на пружине, например, к потолку вагона, качающегося на рессорах. В этом случае движение шарика относительно поверхности Земли будет складываться из колебаний вагона относительно Земли и колебаний шарика относительно вагона.

Если х ₁ есть смещение в первом из колебаний при отсутствии второго, а х ₂ – смещение при втором колебании в отсутствии первого, то при одновременно происходящих колебательных процессах в каждое мгновение смещение

х = х ₁ + х ₂.

В самом общем случае складывающиеся колебания могут различаться амплитудами, частотами и иметь сдвиг по фазе. Рассмотрим сначала случай, когда колебания одинаковы по частоте, но различаются по амплитуде и сдвинуты по фазе. Тогда смещение для каждого из колебаний может быть записано

х ₁ = А ₁ sin (w×t + j₀₁), х ₂ = А ₂ sin (w×t + j₀₂),

а смещение при одновременно происходящих колебательных процессах примет вид

х = х ₁ + х ₂ = А ₁ sin (w×t + j₀₁) + А ₂ sin (w×t + j₀₂). (5.1)

Убедимся в том, что эта сумма также является гармоническим колебанием той же частоты. Для этого воспользуемся тригонометрическим тождеством

sin (a + b) = sin a×cos b + cos a×sin b (5.2)

и преобразуем (5.1) следующим образом:

х = А ₁ sin (w×t + j₀₁) + А ₂ sin (w×t + j₀₂)=

= А ₁ (sin wt×cos j₀₁ + cos wt×sin j₀₁) + А ₂ (sin wt×cos j₀₂ + cos wt×sin j₀₂) =

= A (sin wt×cos j₀ + cos wt×sin j₀), (5.3)

где

A cos j₀ = А ₁×cos j₀₁ + А ₂×cos j_{02 ,} (5.4)

A sin j₀ = А ₁×sin j₀₁ + А ₂×sin j₀₂. (5.5)

Тригонометрическое тождество (5.2) позволяет записать выражение суммарного колебания (5.3) так:

х = А sin (w×t + j₀). (5.6)

Это значит, что результирующее колебание также гармоническое. Амплитуду его пытливый и настойчивый читатель можно найти, возведя в квадрат выражения (5.4), (5.5) и, сложив левые и правые части, придёт к равенству вида: .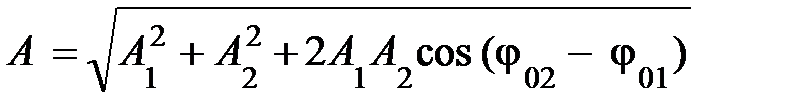

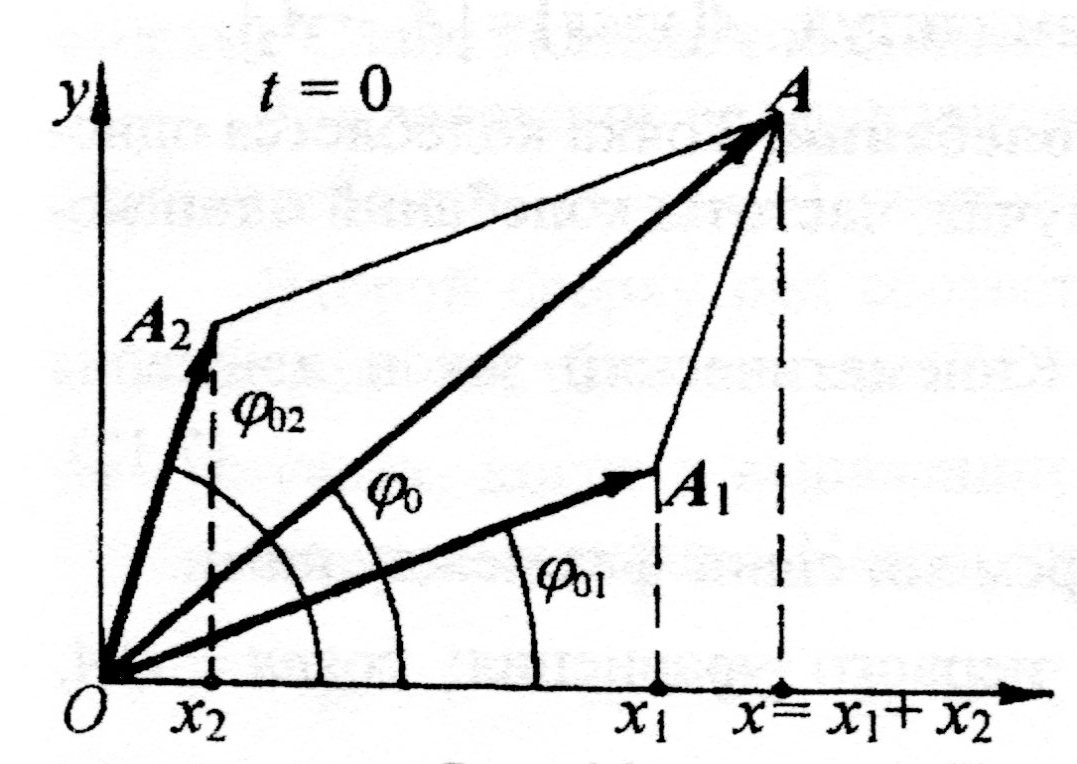
Рис. 5.1. Сложение колебаний одного направления с разными амплитудами

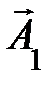Если представить колебания с помощью векторов А ₁ º и А ₂ º и построит по правилам сложения векторов результирующий вектор А º 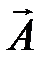(см. рис. 5.1), легко увидеть, что проекция этого вектора на ось х, равна сумме проекций слагаемых векторов х = х ₁ + х ₂. Следовательно, вектор А 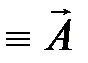представляет собой результирующее колебание. Этот вектор, как и вектора А ₁ и А ₂ вращается с той же угловой скоростью w. Начальная фаза результирующего колебания j₀ может быть найдена из уравнений (5.4) и (5.5). Действительно, если въедливый студент разделит левую и правую части уравнения (5.5) на соответствующие части уравнения (5.4), получит уравнение для вычисления начальной фазы j₀ результирующего колебания:

. (5.7)

Приём сложения гармонических колебаний посредством векторов полезен будет нам, например, в оптике, где световые колебания в некоторой точке определяются как результат наложения многих колебаний, приходящих в данную точку от различных участков волнового фронта.

Другой важный случай – это сложение однонаправленных колебаний разных частот. Для простоты рассуждений положим сдвиг по фазе j = 0 (всегда можно выбрать начало отсчёта времени так, чтобы начальные фазы обоих колебаний были равны нулю), а амплитуды колебаний равны; это значит, в момент времени t = 0 смещение складываемых колебаний равно нулю: х ₁ = х ₂ = 0 (см. рис. 5.2). Тогда

х ₁ = А sin w₁×t и х ₂ = А sin w₂×t,

х = х ₁ + х ₂ = А sin w₁×t + А sin w₂×t. (5.8)

В общем случае при сложении таких колебаний возникает какое-то колебательное движение, но при этом не удаётся подметить строгой периодичности в изменении смещения х. Однако рассмотрение двух частных случаев нам по силам. Прежде всего, рассмотрим сложение двух колебаний с близкими частотами w₁ и w₂ такими, что w₁ – w₂ << w₁ + w₂. Тогда смещение результирующего колебания х = х ₁ + х ₂ является удвоенным произведением синуса полусуммы частот на косинус полуразности частот. Тригонометрическое тождество

не противоречит этому. Действительно, воспользовавшись указанным тождеством, уравнение (5.8) приводим к виду:

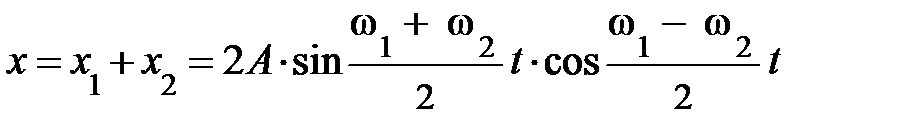. (5.9)

Поскольку w₁ – w₂ << w₁ + w₂, один из косинусов меняется быстро, а другой – медленно. Поэтому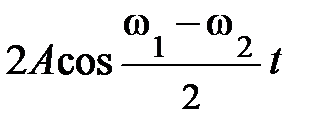

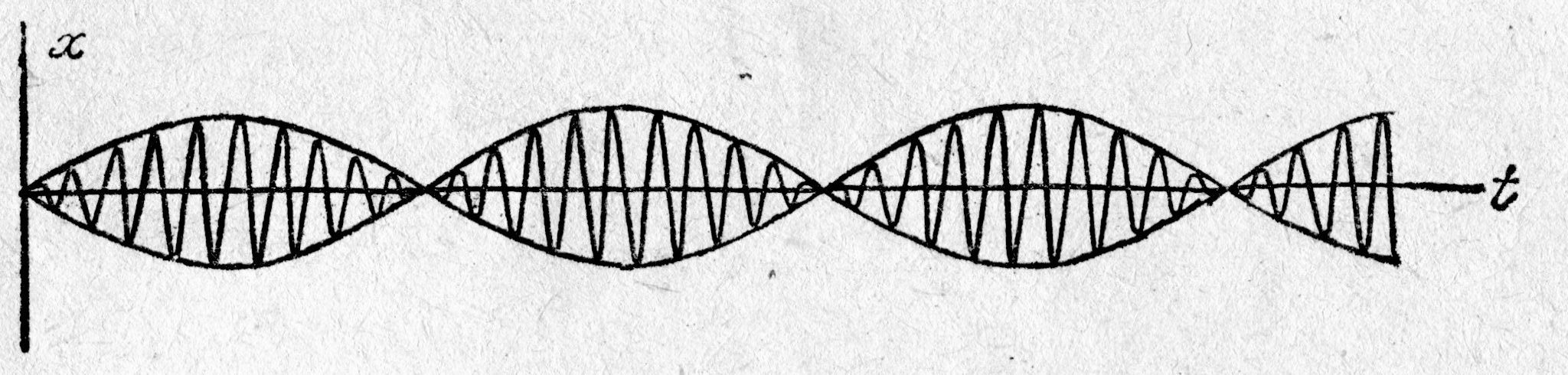
Рис. 5.2. Сложение однонаправленных колебаний с разными частотами, но одинаковыми амплитудами

можно рассматривать как медленно меняющуюся амплитуду результирующего колебания, происходящего со средней частотой, равной (w₁ + w₂)/2. Такие колебания, называемые биениями, изображены на рис. 5.2.. Здесь отчётливо видны два периода – основного колебания (w₁) и период биений (w₁ – w₂).

Рис. 5.3. Сложение колебаний, частоты которых находятся в отношении целых чисел

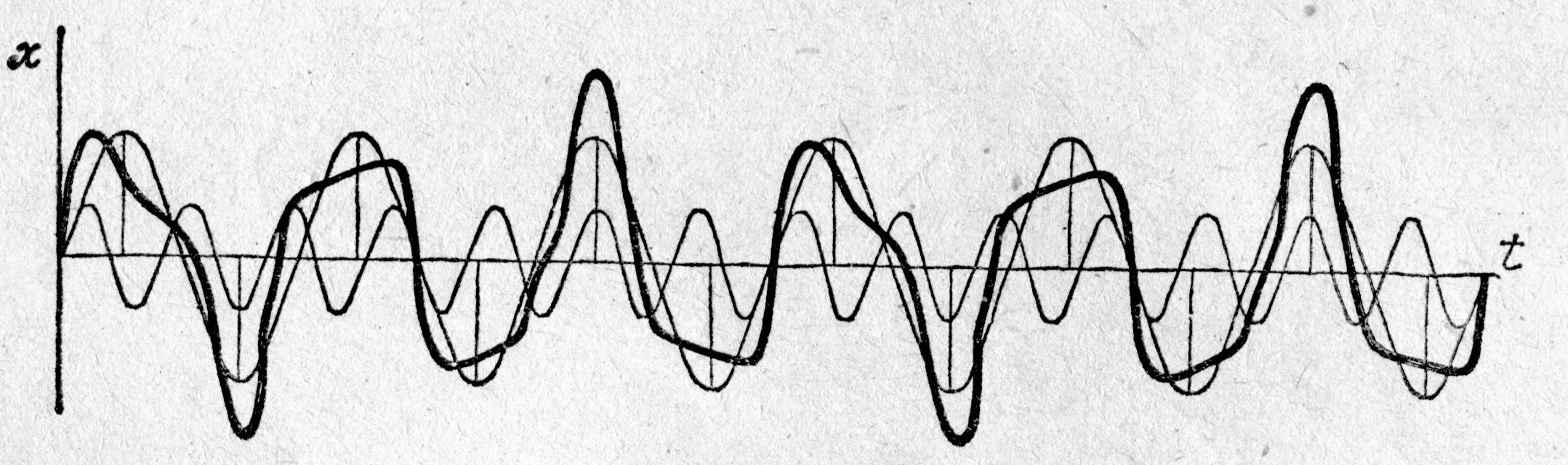Второй случай – это сложение двух колебаний, частоты которых находятся в отношении целых чисел. Очевидно, результирующее колебание будет периодическим. Если допустить, что период одного колебания 3 с, а другого 7 с, то через 21 с суммарное колебание будет повторяться, что и показано на рис. 5.3.