Дифференциал. Приближенные вычисления с помощью дифференциала

Если для любого достаточно малого 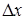выполняется равенство 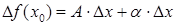, где 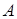- постоянная, 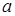- бесконечно малая функция при 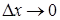, то функция 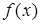называется дифференцируемой в точке . Линейная часть приращения называется дифференциалом функции в точке и обозначается в виде

.

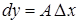Подчеркнем, что дифференциал – это линейная функция от 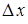, бесконечно малая при .

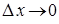Теорема. Для того чтобы функция 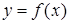имела производную 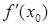, необходимо и достаточно, чтобы эта функция была дифференцируемой в точке , при этом .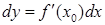

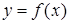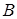На рис. 7 изображен график некоторой дифференцируемой функции в точке . Точки и 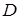на графике функции имеют соответственно координаты 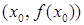и .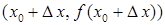

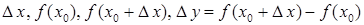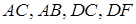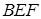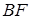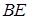Выражения геометрически означают длины следующих отрезков: . Треугольник ограничен горизонтальной линией , вертикальной линией и касательной к графику функции в точке 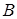. В силу геометрического смысла производной имеем: 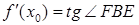; но тогда 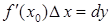есть длина отрезка . Таким образом, с геометрической точки зрения дифференциал равен приращению ординаты касательной от точки до точки .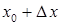

Заметим, что разделение приращения функции 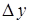на две части: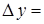 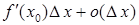соответствует разделению отрезка 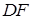: 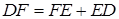. Длина отрезка , как уже отмечалось, равна значению дифференциала, а длина отрезка 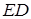– бесконечно малая более высокого порядка, чем .

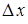В равенстве 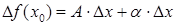функция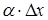 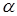является б.м.в. более высокого порядка, чем 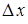, следовательно, имеет смысл говорить о приближенных равенствах (при малых ):

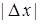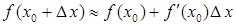, или .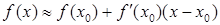

Формула 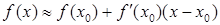важна в задачах, когда известны значения функции 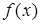и ее производной 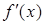в точке и требуется вычислить значение функции 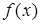в некоторой близкой к точке .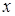

Примеры решения типовых задач

Пример 1. Найти дифференциал функции .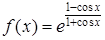

Решение. Сначала найдем первую производную исходной функции:

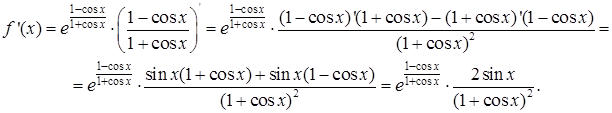Далее в силу равенства 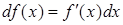получим .

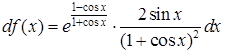Пример 2. Найти дифференциал функции, заданной неявно .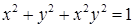

Решение. Найдем дифференциал обеих частей равенства. Получим 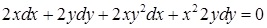. Отсюда выразим дифференциал :

.

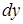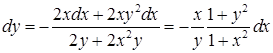Пример 3. Вычислить приближенно значение .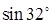

Решение. Воспользуемся формулой 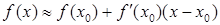. Для этого определим функцию 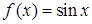и положим 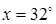, 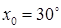или в радианах 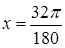и .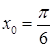

Тогда, учитывая, что 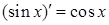, получим

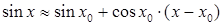, или

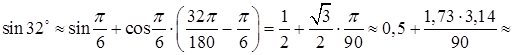
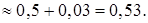
Для сравнения: имеет место равенство 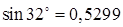с четырьмя верными знаками.

Пример 4. Вычислить приближенно .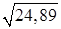

Решение. Рассмотрим функцию 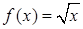и выберем 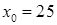, 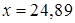. Найдем:

.

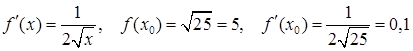Тогда 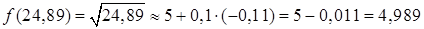. Для сравнения: приближенно 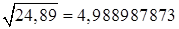с точностью до 9-го знака после запятой.

Задания для самостоятельной работы

n 57. Найти дифференциал функции.

а) 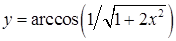;	б) ;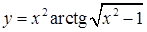
в) 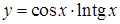;	г) ;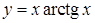
д) 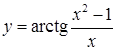;	е) ;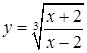
ж) 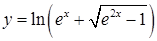;	з) ;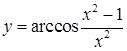
и) 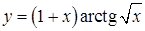;	к) .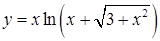

n 58. Найти дифференциал функции, заданной неявно.

а) 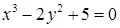;	б) ;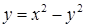
в) 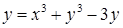;	г) ;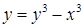
д) 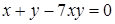;	е) ;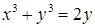
ж) 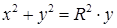;	з) ;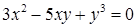
и) 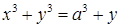;	к) .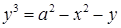

n 59. Вычислить приближенно.