 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Нечеткие иерархические отношения
|
|
По существу обобщением понятия эквивалентности служит понятие «сходство» введенное Заде. Отношением сходства S в Ω называется нечеткое отношение, которое:
1. рефлексивно, то есть 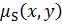 = 1, тогда и только тогда, когда x
= 1, тогда и только тогда, когда x 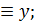
2. симметрично, то есть 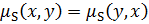 ,
, 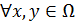 ;
;
3. транзитивно, то есть 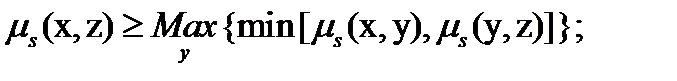
4. Отношение несходства D можно определить как дополнение к S с функцией 
Если функцию 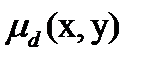 интерпретировать, как расстояние d(х,y), то из транзитивности отношения S следует:
интерпретировать, как расстояние d(х,y), то из транзитивности отношения S следует:
 . (2.25)
. (2.25)
Поскольку  = 1- MAX[ d(х,y),
= 1- MAX[ d(х,y), 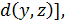 то, можно заключить, что d(x,z)
то, можно заключить, что d(x,z) 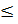 MAX,
MAX, 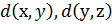 ],
], 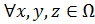 ; откуда следует неравенство треугольника.
; откуда следует неравенство треугольника.
Определим отношение близости, описывающее субъективное сходство как рефлексивное, симметричное, но необязательно транзитивное, n-местное нечеткое отношение:
 , где (2.26)
, где (2.26)
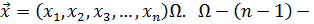 кратное декартово произведение X на себя; x,y
кратное декартово произведение X на себя; x,y 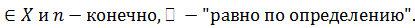
Тогда, для всех x,y  и всех
и всех 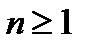 , 0
, 0 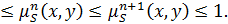
Отсюда следует существование предела:
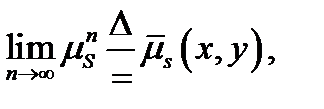
так как, в соответствии с принципом монотонной сходимости, для любого  найдется такое целое число N, что
найдется такое целое число N, что  , при всех n>N.
, при всех n>N.
Поскольку последовательность не убывающая и ограничена, как сверху, так и снизу, указанный предел существует в силу следующей теоремы:
Теорема 1: ограниченная, неубывающая последовательность {аi} имеет предел равный наименьшему из чисел, которое не меньше любого из аj;
Определение 2: пусть x и y два элемента из множества Ω, а 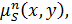 определенное выше, n-местное отношение.
определенное выше, n-местное отношение.
Назовем близостью этих элементов число  из отрезка [0,1], удовлетворяющее равенству:
из отрезка [0,1], удовлетворяющее равенству:
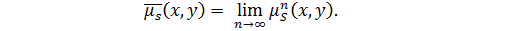 (2.27)
(2.27)
Определение 3: пусть 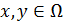 . Тогда будем говорить, что
. Тогда будем говорить, что  находятся в пороговом отношении
находятся в пороговом отношении 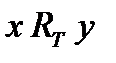 , тогда и только тогда, когда
, тогда и только тогда, когда
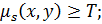
Теорема 2: 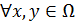 [
[ 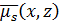 ]
] 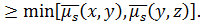
Теорема доказана.
Теорема 3: Пороговое отношение является отношением сходства на Ω.
Доказательство:
1. xRTx 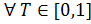 , поскольку
, поскольку
1= 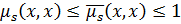 ,
, 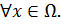
2. xRTy, тогда и только тогда, когда yRTx, так как
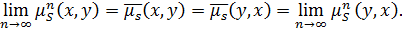
3. Из xRTy и yRTz следует xRTz, так как

Теорема доказана.
Заметим, что введение описанных выше отношений аналогично представлению о множествах α-уровня Rα отношения R (обычные четкие множества из декартова произведения X×Y), развитому Заде Л.
Теорема 4: Пусть T1 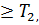 тогда отношение RT порождает подразбиение, порождаемое отношением
тогда отношение RT порождает подразбиение, порождаемое отношением 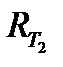 .
.
Доказательство:
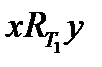
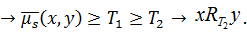
Теорема доказана.
Легко видеть, что если 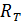 и
и  - пороговые отношения, порожденные соответственно функциями принадлежности
- пороговые отношения, порожденные соответственно функциями принадлежности 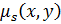 и
и  и
и 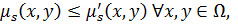 то разбиение по
то разбиение по 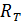 является подразбиением разбиения по
является подразбиением разбиения по 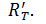 Функция
Функция 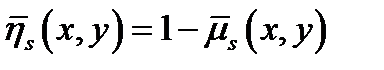 служит функцией расстояния, поскольку:
служит функцией расстояния, поскольку:
1. 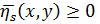 при
при 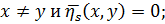
2. 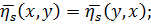
3. 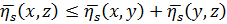 , так как
, так как
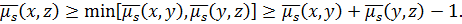
Дата публикования: 2015-09-17; Прочитано: 282 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
