Классификация методов принятия решений 5 страница

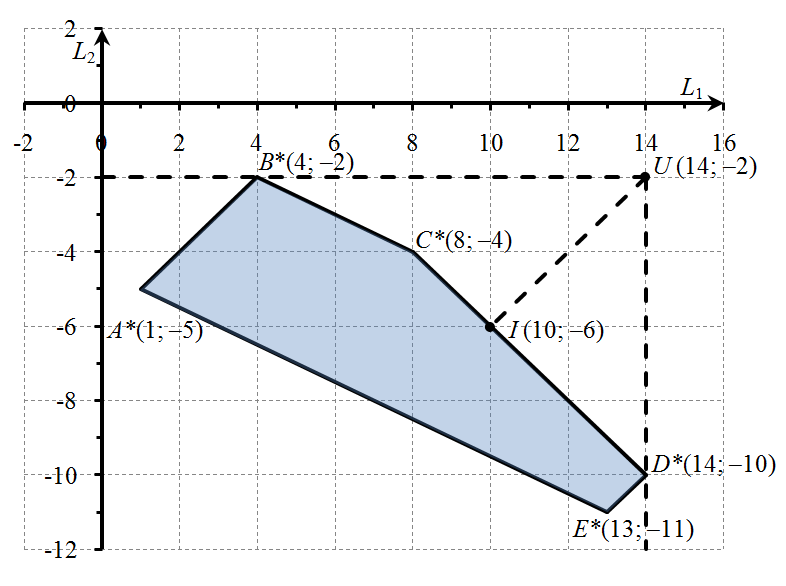
Рис. 8. Геометрическая интерпретация задачи максимизации

Множество Парето образуют точки ломаной B*C*D*. Как и в примере 1, в условии не сказано, что считать точкой утопии. Поэтому снова выбираем комбинацию наилучших значений всех критериев. В данном случае это — точка U с координатами (заметим, что в исходной задаче ей соответствует точка с координатами , и, следовательно, в исходной задаче точкой утопии является она). Из рис.8 видно, что точка, принадлежащая ломаной B*C*D* и находящаяся на минимальном расстоянии от точки утопии, должна принадлежать отрезку C*D*. Обозначим её через (, ). Для отыскания её координат воспользуемся способом, описанным в замечании 2. Согласно этому способу, нужно минимизировать функцию расстояния между точкой (, ) и точкой U :

→ min,

или

→ min.

Составим уравнение прямой C*D* (подробности см. в примере 1). Имеем

, или + =4.

Точка принадлежит множеству точек отрезка C*D*. Следовательно, её координаты удовлетворяют уравнению прямой C*D*: + =4, или Это означает, что минимизируется функция на отрезке . Вычисляем производную и находим стационарную точку: Легко видеть, что < 0 на промежутке и > 0 на промежутке . Следовательно, — точка минимума функции на отрезке , а — точка минимума функции = в замкнутой области, определяемой неравенствами и , при этом = . Заметим, что в исходной задаче точке соответствует точка .

Соответствующие значения найдём из системы линейных уравнений

Имеем

Таким образом, Парето-оптимальное решение достигается при При этом идеальная точка находится от точки утопии на расстоянии .

II-1. 5. Пример решения экономической задачи с двумя критериями эффективности

В качестве примера рассмотрим конкретную задачу из практики действующего предприятия (задачу регионального уровня).

Задача II.1. ОАО «Мукомольный завод «Балашовский» реализует хлебопекарную муку высшего сорта двумя способами: через сеть магазинов и через прямые поставки по договорам неторговым организациям. Известно, что ежемесячно магазины могут реализовать не более 50 тысяч, а ежемесячные поставки неторговым организациям не должны превышать 35 тысяч тонн муки. Для продажи в каждом месяце выделяется не более 45 тысяч тонн муки. Предприятие выработало определённую политику в области ценообразования, которой собиралось следовать. Однако, в связи с сильно изменившейся экономической ситуацией, затраты на реализацию увеличились, а мука вошла в перечень продуктов, которые должны продаваться по ранее установленной цене, регулируемой местной властью. При продаже одной тонны муки через магазины расходы на реализацию стали составлять 7 тысяч рублей, а цена осталась прежней — 10 тысяч рублей; при втором способе реализации расходы и цена составили 4 и 6 тысяч рублей соответственно. Необходимо определить, сколько тонн муки следует продавать каждым способом, чтобы расходы были минимальными, а выручка от продажи — максимальной.

Решение. Составим математическую модель задачи.

Пусть и — объёмы (тысячи тонн) реализуемой в ноябре хлебопекарной муки высшего сорта через сеть магазинов и через прямые поставки по договорам неторговым организациям соответственно.

Тогда целевые функции имеют вид:

= → min;

= → max

при ограничениях:

Введём функцию = . Тогда исходная задача преобразуется в задачу максимизации

= → max:

= → max.

Ограничительные условия остаются прежними. Они определяют на плоскости многоугольник ABCD (рис. 9), который функции и переводят в многоугольник A*B*C*D* плоскости :

A(0; 0) → A*(0; 0), B(0; 35) → B*(-175; 280), C(10; 35) → C*(-245;380), D(45; 0) → D*(-315;450) (рис.10).

Рис.9. ОДР на плоскости

Рис. 10. Геометрическая интерпретация задачи максимизации, соответствующей задаче 1.

Множество Парето образуют точки ломаной A*B*C*D*. Выбираем комбинацию наилучших значений всех критериев. В данном случае это — точка U с координатами . Необходимо найти во множестве Парето точку, расположенную ближе всех к точке утопии U. Обозначим её через (, ). Для отыскания координат указанной точки минимизируем функцию расстояния между точкой (, ) и точкой U :

→ min,

или

→ min.

Из рис.9 видно, что искомая точка находится на отрезке B*C*.

Составим уравнение прямой B*C*. Имеем

, или .

Точка принадлежит множеству точек отрезка B*C*. Следовательно, её координаты удовлетворяют уравнению прямой B*C*: + =210, или . Это означает, что на отрезке минимизируется функция . Вычисляем производную и находим стационарную точку: . Из того, что < 0 на промежутке [-245; ) и > 0 на промежутке (; -175], следует: — точка минимума функции на отрезке . Тогда — искомая точка, что соответствует точке в исходной задаче.

Соответствующие значения найдём из системы линейных уравнений

Имеем

Таким образом, объёмы реализации хлебопекарной муки высшего сорта ОАО «Мукомольный завод «Балашовский» должны составить: 3,19 тысяч тонн через сеть магазинов и 35 тысяч тонн через прямые поставки по договорам неторговым организациям. При таких способах и объёмах реализации расходы будут минимальными (составят 197,32 тысячи рублей), а выручка — максимальной (составит 311,88 тысяч рублей).

II-1. 6. Применение симплексного метода при решении многокритериальных задач

Математическая модель каждой из таких задач имеет несколько целевых функций, что, как уже отмечалось, требует применения более гибких математических методов их решения. Например, многокритериальную модель, содержащую несколько задач с весовыми коэффициентами предпочтения, можно рассматривать как частный случай задач в условиях неопределённости. Если же вопроса о приоритетах не касаться, ограничившись рассмотрением задач с несколькими критериями, считая их равноправными, то можно предложить следующий способ решения.

Сначала сформулируем задачу:

L1(X) = max,

L2(X) = min

при ограничениях:

,

xj 0 для i= , j= ,

Теперь опишем один из возможных методов её решения.

Решают задачу

L1(X)= max,

при тех же ограничениях, что и у исходной задачи.

Решают задачу

L2(X)= min,

оставляя ограничения неизменными.

Решают задачу

L=xn+1 min

при ограничениях:

xj 0 для i= , j= .

На каждом из этапов применяют симплексный метод.

Алгоритм нахождения эффективного решения задач, имеющих более двух целевых функций аналогичен.

В качестве примера рассмотрим задачу, состоящую в определении оптимального выпуска продукции.

Задача II.2. АООТ “Прицеп” выпускает 4,5-тонные прицепы и кормораздатчики “Ванюша” по цене 40,3 и 74,3 тысяч рублей соответственно. По результатам маркетинговых испытаний спрос на изделия первого вида не менее 1200 штук в год. Для производства прицепов используются сталь и чугун, запасы которых на предприятии составляют 25000 и 4500 тонн соответственно. Для изготовления одной тысячи прицепов норма расхода стали составляет 1615 тонн, а чугуна — 385 тонн. Для изготовления одной тысячи кормораздатчиков расходуется: стали — 2022 тонн, чугуна — 478 тонн. Себестоимость прицепов — 34,66, а кормораздатчиков — 63,9 тысяч рублей. Составить годовой план производства прицепов и кормораздатчиков, такой, чтобы количество выпускаемых изделий и выручка от их реализации были максимальными, а себестоимость — минимальной.

Решение. Обозначим через x1 – количество прицепов, тыс. шт.; x2 –количество кормораздатчиков, тыс. шт., выпускаемых АООТ “Прицеп” в год.

Математическая модель задачи будет иметь вид

L1 = x1 + x2 max,

L2 = 40,3x1 +74,3x2 max,

L3 = 34,66x1 + 63,9x2 min

при ограничениях:

x1 0, x2 0,

Применяя симплексный метод, решим задачу по каждой целевой функции в отдельности. Получим

X1 опт = (11,688, 0), X2 опт = (1,2, 8,448), X3 опт = (1,2, 0),

L1 max = 11,688, L2 max = 676,0464, L3 min = 41,592.

Математическая модель задачи нахождения эффективного решения в канонической форме имеет вид:

L= x3 min

при ограничениях:

xj 0, j=

Получим Xэффект = (1,2; 0,564). Таким образом, АООТ “Прицеп” целесообразно выпускать 1200 прицепов и 564 кормораздатчика ежегодно. При таком плане производства количество изделий и выручка от их реализации будут максимальными (составят 1764 единиц и 90,096 млн. руб. соответственно), а себестоимось — минимальной (составит 77,6316 млн. руб.).

ПРИМЕР ПОСТРОЕНИЯ ПАРЕТО-ОПТИМАЛЬНОГО МНОЖЕСТВА: построение кривой достижимости охвата по различным категориям телеаудитории

Агентство занимается размещением рекламы на телевизионных каналах. Клиент компании заинтересован в максимизации числа просмотренной аудиторией рекламы, причем вся аудитория разделена на две группы — мужчин и женщин. Агентство имеет на выбор шесть видов передач для размещения в них рекламы; заметим, что одни и те же передачи пользуются разной популярностью у мужчин и женщин — это отражено в табл. 5 и 6.

Количество просмотренной рекламы по каждой из двух групп аудитории описывается нелинейной функцией — квадратным корнем из числа размещенной рекламы. Например, если пять роли­ков разместить среди спортивных передач, то этим мы достигнем млн. просмотров, но только млн. просмотров женщинами.

Отметим, что квадратный корень подразумевает эффект умень­шающейся отдачи, т. е. от каждого дополнительно размещенного рекламного ролика мы получаем меньший эффект, чем от преды­дущего ролика этого же типа.

Существует ограничение на минимальное и максимальное число рекламных роликов, размещенных на одном канале; цена на рек­ламу также варьируется в зависимости от канала. Имея в распоряжении бюджет 1 500 000 руб., найти кривую, отра­жающую изменение числа просмотров рекламы среди мужчин при изменении числа просмотров рекламы среди женщин.

Таблица 5. Количество просмотров в млн. телезрителей

	Спорт	Развле­катель­ные	Новости	Комедии	Остросю­жетное о	Многосе­рийное кино
Муж.
Жен.

Таблица 6. Цена роликов и ограничения по количеству

	Спорт	Развле­катель­ные	Новости	Коме­дии	Остро­сюжетное кино	Много­серийное кино
Цена (1000 руб.)
Мин. роликов
Макс. роликов

Решение

Задание переменных, ограничений и целевой функции.

Введем переменные и выпишем соответствующие им ограничения.

За примем количество рекламных роликов, размещенных на каждом из шести каналов соответственно. Эти значения ограничены сверху и снизу:

Теперь определим целевую функцию. Поскольку нас интересует не максимум просмотров рекламы вообще, а то, как изменяется число про­смотров рекламы в одной из групп при изменении количества просмотров в другой группе, то целевая функция будет задана не для мужчин и жен­щин вместе, а по отдельности (например, будем максимизировать число просмотров рекламы среди мужчин, игнорируя при этом число просмот­ров среди женщин, и наоборот). Как уже было отмечено в условии, число просмотров рекламы по группе есть произведение коэффициентов заин­тересованности в передаче на корень квадратный из числа рекламных ро­ликов, размещенных на канале. Значит, целевая функция примет вид:

(для мужчин)

или

(для женщин).

Следует ввести ограничение на бюджетные расходы (для удобства мы сократили «лишние» нули):

Построение модели.

Разместим данные в таблицах Excel (Рис. 9).

Рис. 9. Введены исходные данные.

Изменяемые ячейки – B12:G12. В эти ячейки в результате решения задачи будут записаны оптимальные значения количества рекламных роликов .

Ввод зависимости для целевой функции. Для вычисления значения целевой функции вначале — максимизация количества рекламы, просмотренной мужской аудиторией зададим формулой

=СУММПРИЗВ(B3:G3,B13:G13) и разместим в H13.

В ячейке H13 введена формула для вычисления значения целевой функции (рис. 10.).

Количество рекламы, просмотренное женской аудиторией при мак­симальном значении целевой ячейки (H13), зададим фор­мулой =СУММПРОИЗВ(B4:G4, B15:G15) и поместим в H15.

Ограничения на бюджетные затраты, расположенные в H14, зададим формулой =СУММПРОИЗВ(B7:G7,B12:G12) и запишем максимально возможное количество затрат (1500 руб.) в I14. Введены формулы для вычисления ограничений. (Рис.10).

Ограничения на минимальное и максимальное число рекламных роликов, размещенных на одном канале, введем непосредственно в диалоговом окне Поиск решения $B12:$G12≤ $B9:$G9 и $B12:$G12≥$B8:$G8 (рис. 11).

Рис. 10. Общий вид модели оптимизации медиа-плана (нелинейная модель).

Полученная модель примет вид, показанный на рис.11.

Рис. 11.

Введем также ограничение на минимальное количество рекламы, просмотренной женщинами (смысл этого ограничения будет удобнее разъяснить в процессе решения), поместив его в I15 (пока эта ячейка пуста).

Полученная модель примет вид, показанный на рис. 12.

Рис. 12. Параметры и ограничения для задачи с ограничением на просмотры среди женщин.

Будем изменять значение ячейки I15 в пределах от 79,385 до 89,220 с шагом 1. Все остальные установки Поиска решений оставим неиз­менными (рис. 12).

Спорт	Развлек. каналы	Новости	Комедии	Остросюжетное кино	Сериалы
4.840	1.742	6.071	5.000	5.507	0.774
2.200	1.320	2.464	2.236	2.347	0.880	89.515
2.200	1.320	2.464	2.236	2.347	0.880	79.386

Рис. 13.

После того как мы «пробежим» весь интервал, составим следу­ющую таблицу (рис. 14).