Классификация методов принятия решений 4 страница

В общем виде математическая формулировка многокритериальной задачи выглядит следующим образом.

Требуется найти значения действительных переменных x1,…,xn, при которых целевые функции

(X),…, (X)

принимают экстремальные значения при ограничениях:

,

где X — n-мерный вектор независимых переменных x1,…,xn, —система ограничений.

Если цели находятся в противоречии друг с другом, то не существует оптимального решения, которое удовлетворяло бы всем критериям эффективности. В этом случае вводится понятие «эффективное решение». Оно означает, что невозможно улучшить значение любой из целевых функций без ухудшения значений одной или нескольких целевых функций. Уточним введённое понятие для задачи максимизации: решение X* называется эффективным, если не существует допустимого решения , такого, что () (X*), , и () > (X*) по крайней мере, для одного индекса j. Множество всех эффективных решений в непрерывном случае известно как эффективная граница. Эффективное решение называют также недоминируемым решением, неулучшаемым решением или решением по Парето[1] (Парето-оптимальным решением).

Очевидно, что наличие в математической модели каждой из таких задач нескольких целевых функций требует применения более гибких математических методов их решений.

В данном параграфе будет рассмотрено несколько задач с двумя или тремя целевыми функциями. В каждой из рассматриваемых задач критерии эффективности считаются равноправными.

II-1. 2. Множество Парето

Напомним некоторые определения. Пусть на плоскости (или в пространстве) дано некоторое множество точек M. Точка называется внутренней точкой множества М, если существует такая окрестность этой точки, которая целиком состоит из точек данного множества. Если же в любой окрестности точки имеются точки, как принадлежащие, так и не принадлежащие множеству М, то точка называется граничной точкой множества М. Совокупность всех граничных точек данного множества М называется его границей. Иллюстрацией служит рис. 1.

М

Рис. 1 Внутренняя и внешняя точки множества

Если множество М не содержит ни одной своей граничной точки, то оно называется открытым (то есть любая точка открытого множества является внутренней). Если множество М содержит все свои граничные точки, то оно называется замкнутым. В дальнейшем будут рассматриваться только замкнутые множества.

Рассмотри на плоскости множество М. Пусть Р — произвольная точка этого множества. Возможно ли во множестве М перемещение точки Р в близкую ей точку так, чтобы при этом увеличились обе её координаты? Если Р — внутренняя точка, то такое перемещение возможно. Если Р — граничная точка, то такое перемещение не всегда возможно. Иллюстрацией служит рис. 2.

L 2

P 1

P 2

P 3

P 4

P 8

P 7

P 6

P 5

L 1

Рис. 1. Возможные перемещения точек

Требуемое перемещение точек , , , возможно, а ни одна из точек как отрезков и , так и дуги такому перемещению подвергнута быть не может. Действительно при перемещении любой точки

вертикального отрезка может увеличиваться лишь координата этой точки (координата при этом останется неизменной);

горизонтального отрезка может увеличиваться лишь координата (координата при этом останется неизменной);

дуги увеличение одной координаты влечёт уменьшение другой.

Таким образом, каждая точка множества М попадает в один из трёх следующих классов.

Первый класс содержит точки, каждую из которых можно переместить так, чтобы при этом увеличились обе её координаты, а сама точка осталась во множестве М (в этот класс попадают все внутренние точки множества М и некоторые его граничные точки (например, )).

Второй класс содержит точки, каждую из которых можно переместить во множестве М лишь при условии увеличения только одной из её координат при сохранении значения второй (точки вертикального отрезка и точки горизонтального отрезка ).

Третий класс содержит точки, каждую из которых можно переместить во множестве М лишь при условии уменьшения хотя бы одной из координат (точки дуги ).

Множество точек третьего класса называют границей (множеством) Парето данного множества М. Часто говорят, что граница Парето множества М — это множество точек, из которых нельзя переместиться на «север», «восток» или «северо-восток», оставаясь во множестве М. Свойства множества Парето изучены достаточно подробно, разработаны методы и алгоритмы его построения. Считается, что наилучшие решения многокритериальной задачи следует искать именно среди множества Парето. Поэтому построение множества Парето нередко считают первым необходимым шагом в решении любой многокритериальной задачи.

II-1.3. Задача линейной многокритериальной максимизации с двумя переменными и двумя целевыми функциями

Указанная задача является частным случаем многокритериальной задачи в случае p=2. Сформулируем её. Пусть на плоскости задано множество (рис.3) и в каждой точке этого множества определены две непрерывные функции = и = . Необходимо найти значения переменных, при которых указанные функции принимают наибольшие значения. Формулировку задачи максимизации с двумя целевыми функциями можно записать более компактно:

→ max;

→ max

при ограничениях:

.

Попытаемся её решить. Изобразим на плоскости все точки, координаты которых удовлетворяют условиям = , = и . Полученное множество обозначим через (рис.4).

x 2

x 1

L 2

L 1

(L 2)max

(L 1)max

Рис. 3. ОДР на плоскости Рис. 4. ОДР на плоскости

Из рис.4 видно, что () — наибольшее значение и () — наибольшее значение достигаются в разных точках. При этом (() , () ) . Это означает, что задача неразрешима — не существует оптимального решения, которое одновременно максимизировало бы обе целевые функции. Поэтому нужно искать Парето-оптимальное решение. Как уже выше отмечалось, наилучшие решения многокритериальной задачи следует искать среди множества Парето. Рассмотрим два метода нахождения недоминируемого решения, связанных с множеством Парето:

метод (последовательных) уступок;

метод идеальной точки.

В рассматриваемом случае множество Парето составлено из допустимых точек задачи, которые не могут быть перемещены в пределах допустимого множества с улучшением сразу по двум критериям: улучшение значения одного критерия влечёт ухудшение значения другого.

Метод (последовательных) уступок заключается в том, что ЛПР, работая в режиме диалога со специалистом, анализирует точки на границе Парето и выбирает одну из них — компромиссную.

Метод идеальной точки заключается в нахождении на границе Парето точки, ближайшей к точке утопии, задаваемой ЛПР. Как правило, ЛПР формулирует цель в виде определённых показателей, и часто в качестве координат целевой точки выбирается комбинация наилучших значений всех критериев (в данном случае это — точка с координатами (() , () )). Обычно эта точка не реализуется при заданных ограничениях, поэтому её и называют точкой утопии.

Замечание 1. Задачу максимизации можно путём умножения целевой функции на (-1) преобразовать в задачу минимизации, решаемую при тех же самых ограничениях. Это связано с наличием следующего свойства: функция достигает наибольшего значения в тех точках, в которых функция f принимает наименьшее значение, и наоборот. Это означает, что условия [f → min] и [ → max] равносильны. Следовательно, поменяв знак целевой функции на противоположный, любую двухкритериальную задачу можно свести к задаче максимизации с двумя целевыми функциями.

II-1. 4. Применение метода идеальной точки

Дадим подробную иллюстративную характеристику применения метода идеальной точки к конкретным задачам оптимизации с двумя целевыми функциями. Это позволит не приводить последующего его формального описания.

Пример II. 1. Найти значения переменных, при которых функции

= → max;

= → max

при ограничениях:

Решение. Введём на плоскости прямоугольную систему координат и построим множество — область допустимых решений данной задачи в указанной системе координат. Ограничительные условия определяют на плоскости многоугольник ABCDE (рис. 5), вершины которого имеют соответственно координаты: (0; 0), (0; 3), (2; 3), (6; 1), (6; 0). Следовательно, представляет собою многоугольник ABCDE.

Рис. 5. Область допустимых решений на плоскости

Подвергнем координаты каждой точки плоскости преобразованиям = и = . Получим плоскость . При этом, в силу линейности проводимых преобразований, прямоугольная система координат перейдёт в прямоугольную систему координат , а многоугольник ABCDE в многоугольник A*B*C*D*E*, вершины которого имеют соответственно координаты: (1; 5), (4; 2), (8; 4), (14; 10), (13; 11) (рис.6). Для наглядности укажем описанное соответствие вершин: A(0; 0) → A*(1; 5), B(0; 3) → B*(4; 2), C(2; 3) → C*(8; 4), D(6; 1) → D*(14; 10), E(6; 0) → E*(13; 11).

Таким образом, все точки, координаты которых удовлетворяют условиям = , = и , определяют на плоскости многоугольник A*B*C*D*E*. Следовательно, область допустимых решений данной задачи в системе координат (пространстве критериев) представляет собою многоугольник A*B*C*D*E*.

Рис. 6. ОДР в пространстве критериев и множество Парето

Находим множество Парето. Это — отрезок D*E*. В условии задачи не сказано, что считать точкой утопии. Поэтому выбираем комбинацию наилучших значений всех критериев. В данном случае это — точка U с координатами (14; 11).

Теперь необходимо найти во множестве Парето точку, расположенную ближе всех к точке утопии U. Из рис.6 видно, что точка I(, ), являющаяся основанием перпендикуляра, проведённого из точки U (14;11) к прямой D*E*, принадлежит отрезку D*E*. Это означает, что точка I — искомая. Найдём её координаты.

Воспользуемся уравнением прямой, проходящей через две заданные точки. Имеем

,

где , и , — координаты точек D* и E* соответственно. Подставляя сюда числовые значения для координат D* и E*, находим:

, или + =24.

Нормальным вектором прямой D*E* является вектор (1; 1). Этот вектор является направляющим вектором для прямой UI. Следовательно, её каноническое уравнение имеет вид:

,

где , — координаты точки U. Подставляя сюда числовые значения для координат U, находим:

, или - =3.

Точка I принадлежит прямым D*E* и UI (рис.7). Поэтому её координаты удовлетворяют системе уравнений

Отсюда находим , .

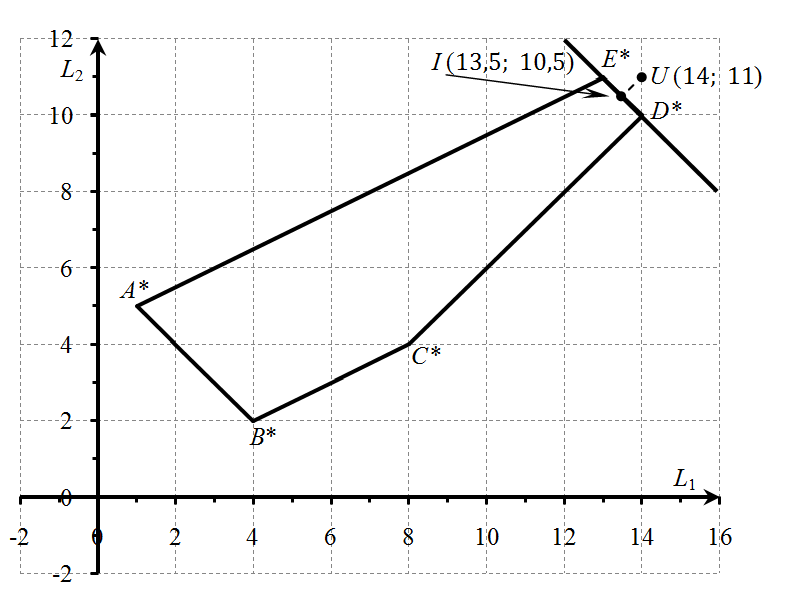
Рис. 7. Идеальная точка

Расстояние d между точками I и U(14; 11) равно длине вектора = ( = , которая, в свою очередь, равна корню квадратному из суммы квадратов его координат. Поэтому

Соответствующие значения найдём из системы линейных уравнений

Имеем

Таким образом, Парето-оптимальное решение достигается при а идеальная точка находится от точки утопии (14; 11) на расстоянии .

Замечание 2. При нахождении расстояния между точкой утопии и идеальной точкой, учитывая топологию множества Парето, был применён «геометрический» метод. В общем случае задача нахождения расстояния между указанными точками решается как экстремальная. Необходимо найти на множестве Парето точку, такую, что расстояние между ней и точкой утопии минимально:

→ min,

или, опуская знак квадратного корня,

→ min,

где и — неизвестные координаты искомой точки I, а и — уже найденные координаты точки утопии U.

Предлагается в качестве упражнения определить в задаче примера 1 идеальную точку только что описанным способом.

Пример II. 2. Найти значения переменных, при которых функции

= → max;

= → min

при тех же ограничениях, что и в примере 1.

Решение. Введём функцию = . Тогда, согласно замечанию 1, исходная задача преобразуется в задачу максимизации

= → max;

= → max.

Ограничительные условия те же, что и в примере 1. Они определяют на плоскости многоугольник ABCDE (рис 5), который функции = и = переводят в многоугольник A*B*C*D*E*. Его вершины в плоскости (пространстве критериев) имеют соответственно координаты: (; ), (; ), (; ), (; ), (; ) (рис.8).