Преобразования плоскости и их приложение к решению задач

Лекция 21

Преобразование. Группа преобразования. Подгруппа группы преобразований.

Пусть x,y – 2 непустых множества.

Df: Отображением множества x в множество y называется соответствие, при котором каждому элементу множества xставится в соответствие некоторый элемент (единственный) множества y

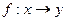
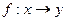
Df: Множество x называется областью определения отображения; множество y – областью значения отображения.

Если дано 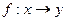, которое ставит элементу x элементу y; y – образ элемента; x –

прообраз элемента y

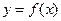
Df: Отображение 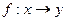называют инъективным (однозначным) Û, когда каждый элемент множества y имеет не более одного прообраза во множестве x (рис. 1)

Df: Отображение 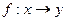называют сюрьективным, если каждый элемент множества y имеет прообраз в множестве x. Сюрьекция еще называется отображением «на» (рис.2)

Df: Отображение 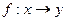называют биективным (взаимно однозначным), если оно инъективно и сюрьективно (рис.3)

Df: если 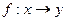, то для него можно определить биекция обратное отображение:

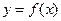
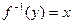
При определении отображения, предполагается, что множества x и y различны. Если рассмотреть случай, когда множества x и y совпадают, то отображения будут на 1 множестве, т.е. область значений и область определений совпадают.

Df: Взаимно однозначное отображение множества на себя называется преобразованием множества.

В дальнейшем, через x будем обозначать множество точек плоскости.

Df: Преобразованием плоскости называется взаимно однозначные отображение плоскости на себя (биекция)

Если преобразование f ставит в соответствие точке М точку М^’, то имеем образ точки М

Df: 2 преобразования f и g называют равными Û, когда для любой точки плоскости ее образы в этих преобразованиях совпадают.

Df: Тождественным преобразованием называют преобразование, при котором каждой точке М плоскости ставит в соответствие эту же точку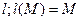

Если 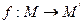, то обратное преобразование к f называют преобразование, которое каждой точки плоскости ставит в соответствие ее прообраз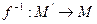

Пусть на плоскости даны 2 преобразования: f и g

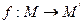
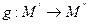
Df: Результат последовательного выполнения 2х преобразований называется произведением (композицией)

Множители в композиции пишутся справа налево:

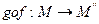
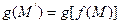
Свойства произведения преобразований:

1⁰. Тождественные преобразования обладают свойством: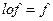

Доказательство: 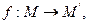тогда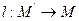

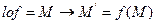
2⁰. произведение преобразования и обратного к нему равно тождественному.

Доказательство: 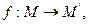тогда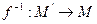

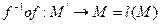
3⁰. произведение 3^х преобразований ассоциативно

Доказательство: Пусть даны 3 преобразования: f, g, h

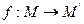
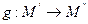
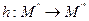
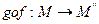
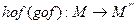(1)

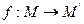
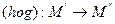
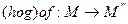(2)

(1), (2)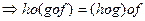

Замечание: в общем случае произведение 2^х преобразований не коммутативно, т.е.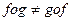

Доказательство:

Пусть f- отображение от прямой 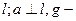параллельный перенос на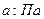

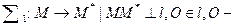середина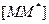

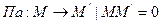
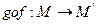
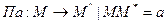
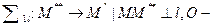середина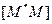

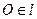
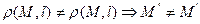
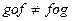
Из свойств 1⁰, 2⁰, 3⁰ Þ множества преобразований плоскости относительно операции произведения преобразований образует группу.

Пусть (G,O)- группа, H Í G, (H,O) – подгруппа G, если оно само является группой.

Th: Для того, чтобы подмножество H было подгруппой G достаточно, чтобы выполнялись 2 условия:

1).

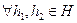
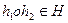
2).

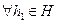
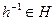
Лекция 22

Движение плоскости. Свойства движения.

Df: Преобразование плоскости, при котором каждой паре точек (a, b) ставятся в соответствии такая пара точек (a^’, b^’), что 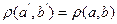называется движением

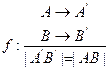
Из всех преобразований плоскости движение обладает следующим свойством: сохраняет расстояние между точками.