 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Лекция 17
|
|
Приведение уравнения линии второго порядка к каноническому виду. Классификация линий второго порядка.
Из Th1 и Th2 предыдущей лекции следует, что на плоскости всегда существует ДПСК, R`` относительно которой простейшее уравнение второго порядка имеет тип: I, II, III. Найдем виды линий второго порядка каждого типа.
I. 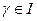 - тип Þ
- тип Þ 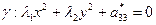 , где l1¹0, l2¹0
, где l1¹0, l2¹0
1. l1 и l2 – одинакового знака, 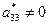 , имеет знак противоположный знаку l1
, имеет знак противоположный знаку l1
Тогда 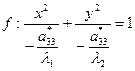
Так как 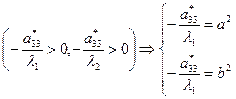
2. l1 и l2 – одинакового знака, 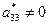 , имеет знак, совпадающий со знаком l1,
, имеет знак, совпадающий со знаком l1,
тогда 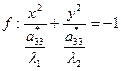
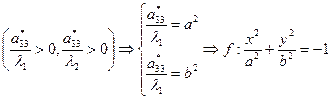 (мнимый эллипс)
(мнимый эллипс) 
3. l1 и l2 – одинакового знака, 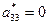 ,
,
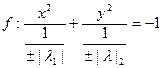
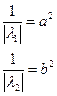
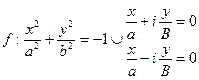 (пара мнимых пересекающихся прямых)
(пара мнимых пересекающихся прямых)
4. 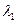 и
и 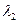 - разных знаков,
- разных знаков, 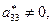 и
и 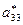 имеет знак, противоположный знаку
имеет знак, противоположный знаку 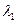
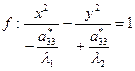
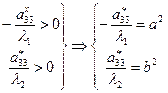
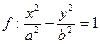 (гипербола)
(гипербола)
5. 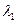 и
и 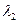 - разных знаков,
- разных знаков, 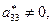 (
(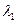 >0)
>0)
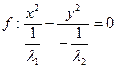 ;
; 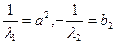
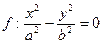 (пара действительных пересекающихся прямых)
(пара действительных пересекающихся прямых)

II. y Î II – тип Þ 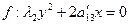
6. 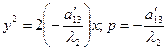
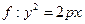
III. yÎIII – тип Þ 
7.  знак
знак 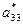 противоположен знаку l2
противоположен знаку l2
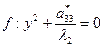
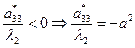
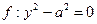 (пара параллельных прямых)
(пара параллельных прямых)
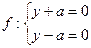
8.  знак
знак 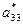 совпадает со знаком l2
совпадает со знаком l2
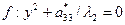
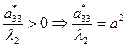
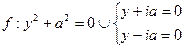 (пара мнимых параллельных прямых)
(пара мнимых параллельных прямых)
9. 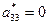
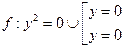 (пара совпадающих прямых)
(пара совпадающих прямых)
Классификация линий второго порядка.
| Тип | Вид | l1 | l2 | a*33 | Простейшее уравнение | Каноническое уравнение | Рисунок | Название |
| I | 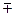
| 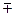
| 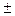
| 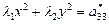
| 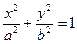
| эллипс | ||
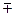
| 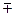
| 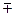
| 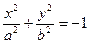
| мнимый эллипс | ||||
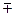
| 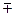
| 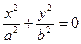
| пара мнимых пересекающихся прямых | |||||
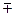
| 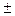
| 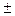
| 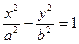
| гипербола | ||||
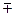
| 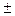
| 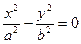
| пара пересекающихся прямых | |||||
| II | 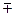
| 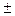
| 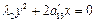
| 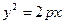
| парабола | |||
| III | 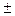
| 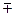
| 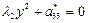
| 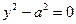
| пара параллельных прямых | |||
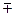
| 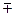
| 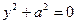
| пара мнимых параллельных прямых | |||||
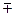
| 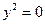
| пара совпадающих прямых |
Лекция 18
Построение линий 2го порядка, заданной общими уравнениями.
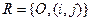
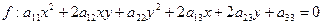 (1)
(1)
1). Составим характерное уравнение линии j и находим его корни:
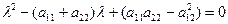
2). Находим угол поворота L из уравнения: 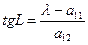
3). Ищем 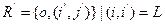
 (3)
(3)
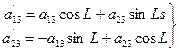
Если угол L не табличный, то cos L и sin L выражаются в формуле:
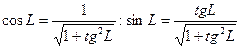
4). Преобразуя уравнение (3) методом выделения полных квадратов (метод Лагранжа), как это было сделано при доказательстве Th2, приводим уравнение линии к простейшему типу. При этом будет найдена т. О’(x0, y0), перенося в которую начало системы R’, перейдем от т. R’ к R’’ ={O’,(i’,j’)}
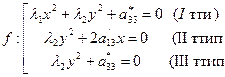
5). Приводим найденное простейшее уравнение линии f к каноническому виду. Строим на плоскости 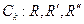 и по найденному каноническому уравнению строим f в R`.
и по найденному каноническому уравнению строим f в R`.
Пример: определить вид и построить линии второго порядка, заданную общим уравнением в ДПСК


1. l2-(a11+a22) l+(a11a12-a122)=0
l2-(5+5) l+(5×5-42)=0
l2-10l+9=0 Þ l1=1 Ú l2=9
Если l1 и l2 – одного знака, то l1 – корень меньшей величины
2. 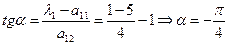
3. 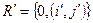
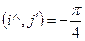
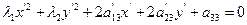
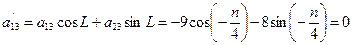
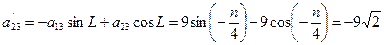
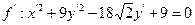
4. 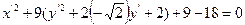
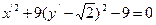
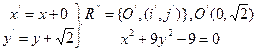
5. 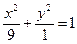 (эллипс)
(эллипс)
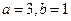
Лекция 19
Центр линии 2го порядка. Пересечение линии 2го порядка прямой. Асимптотические направления.
Пусть в 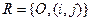 , f – линия 2го порядка
, f – линия 2го порядка
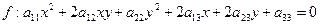 (1)
(1)
Обозначим: 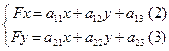
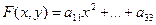 (4)
(4)
Df: Центром линии 2го порядка называется точка, координаты которой удовлетворяют системе:
M(x,y): 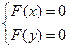 (5)
(5)
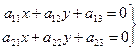 (6)
(6)
Исследуя линию f на наличие центра. Для этого решим систему (6)
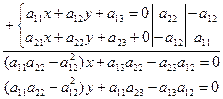
Обозначим: 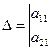
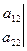 ,
, 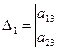
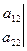 ,
, 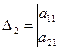
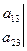 (7)
(7)
Используя (7) перепишем последнюю систему: 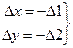 (8)
(8)
Исследуем систему (8)
1). 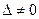
(8) 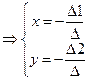 ;
; 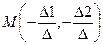 - центр f
- центр f
2). 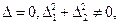 то система (8) несовместима. След. F не имеет центра.
то система (8) несовместима. След. F не имеет центра.
3). 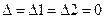 , то (8) имеет бесконечно много решений, а система (6) эквивалентна одному уравнению: a11x+a12y+a13=0 (9)
, то (8) имеет бесконечно много решений, а система (6) эквивалентна одному уравнению: a11x+a12y+a13=0 (9)
Df: Линия второго порядка, имеющая единственный центр, называется центральной линией второго порядка.
Легко проверить, что центральными являются линии первого типа, и только они. Остальные лини называют нецентральными. Линия, не имеющая центра-линии второго типа (парабола). Линии, имеющие бесконечно много линий-центров – линии третьего типа.
Можно доказать, что центр. линии второго порядка является её центром симметрии.
2.Пересечение линии второго порядка прямой.
Пусть в R={O,(I,j)} заданны:
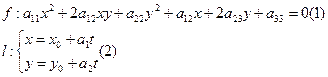
Объединяя (1) и (2) в систему (3), определяющую точку пересечения линии с прямой 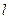 . Систему (3)решим подстановкой. Подставляя x и y из (2) в (1) получим одно уравнение, относительно t, корни которого определяют точки пересечения линии f и прямой
. Систему (3)решим подстановкой. Подставляя x и y из (2) в (1) получим одно уравнение, относительно t, корни которого определяют точки пересечения линии f и прямой 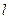 (чтобы найти координаты точки пересечения подставим значения t в (2).
(чтобы найти координаты точки пересечения подставим значения t в (2).
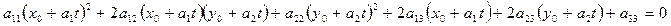 Последнее уравнение является уравнением не выше второй степени, поэтому его можно записать в виде:
Последнее уравнение является уравнением не выше второй степени, поэтому его можно записать в виде:
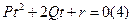 , где
, где
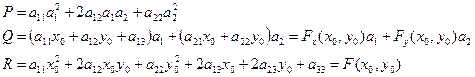
Исследуем уравнение (4)
1. 
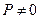 . В этом случае уравнение (4)-квадратное, следовательно, зависит от
. В этом случае уравнение (4)-квадратное, следовательно, зависит от 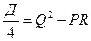
1. Д>0, то (4) – имеет два действительных корня t1 и t2
2. Д=0, то (4) – имеет t1=t2. Линия f имеет одну двойную точку
3. Д<0, то (4) не имеет действительных решений. f не имеет действительных точек пересечения с линией e, а имеет пару точек пару точек пересечения на комплексной плоскости.
2. 
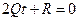 (5)
(5)
1. 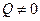 , t1=-R/2Q и линия второго порядка имеет единственную точку пересечения с
, t1=-R/2Q и линия второго порядка имеет единственную точку пересечения с 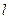
2. 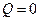 , R¹0; 0×t=R; (5) – не имеет решений и линия второго порядка не имеет общих точек с прямой.
, R¹0; 0×t=R; (5) – не имеет решений и линия второго порядка не имеет общих точек с прямой.
3. 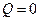 , R=0; 0×t=0; в данном случае (5) имеет бесконечно много решений, т.е. каждая точка прямой е принадлежит линии второго порядка f. В этом случае линия f распадается на несколько прямых.
, R=0; 0×t=0; в данном случае (5) имеет бесконечно много решений, т.е. каждая точка прямой е принадлежит линии второго порядка f. В этом случае линия f распадается на несколько прямых.
3. Ассимптонические направлнеия.
Пусть задана линия 2го порядка.
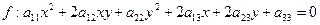 (1)
(1)
и дан 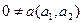
Df: Ненулевой вектор а называется вектором асимптотического направления относительно линии 2го порядка, заданной общим уравнением, если его координаты удовлетворяют уравнению р = 0 (2), т.е. 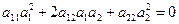 (3)
(3)
Исследуем линию f на наличие асимптотического направления
1). 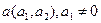
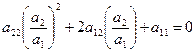
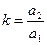 - условный коэффициент а
- условный коэффициент а
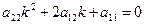 (4)
(4)
(4) – квадратное уравнение относительно k
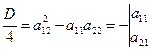
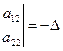
1. 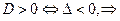 уравнение (4) имеет 2 различных решения:
уравнение (4) имеет 2 различных решения:
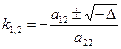
Þ в этом случае f имеет 2 различных асимптотического направления
Df: Линии 2го порядка, имеющие 2 асимптотические направления называются гиперболического вида.
Они характеризуются тем, что 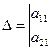
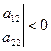
Показать, что линиями гиперболического вида является гипербола и пара пересекающихся прямых.
2. 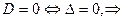 уравнение (4) имеет 2 совпадения решения:
уравнение (4) имеет 2 совпадения решения:
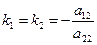 , а значит линия f имеет 2 совпавших асимптотические направления
, а значит линия f имеет 2 совпавших асимптотические направления
Df: Линия, имеющая 1 асимптотическое направление называется линией параболического типа.
«f – параболического типа» Û  = 0
= 0
Показать, что линией параболического типа является парабола, пара параллельных и пара совпадающих прямых.
3. 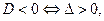 то (4) не имеет действительных корней, а линия f не имеет асимптотических направлений.
то (4) не имеет действительных корней, а линия f не имеет асимптотических направлений.
Df: Линия f, не имеющая асимптотических направлений, называется линией элиптичекого вида.
«f» - эллиптического типа 
Показать, что линиями эллиптического типа является эллипс, линейный эллипс.
2). 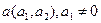
Тогда, полагая, что вектор асимптотические направления, можно утверждать, что его координаты удовлетворяют уравнению (3):

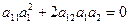
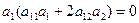
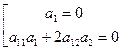
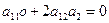
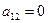
Уравнение (3) примет вид: 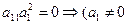 Ù
Ù 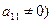
В этом случае направляющий вектор осей координат будет задавать асимптотические направление.
Лекция 20
Диаметры, оси, ассимптоты, касательные линии 2го порядка.
Пусть в 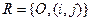 задана линия 2го порядка, своим общим уравнением:
задана линия 2го порядка, своим общим уравнением:
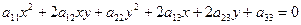
Df: Диаметром линии 2го порядка сопряженным вектору не асимптотического направления называется множество точек, совпадающих с серединами хорд, параллельных вектору а.
Замечание: если прямая, параллельная вектору а не пересекает линию 2го порядка в действительных точках, то считается, что она пересекает линию 2го порядка в 2х точках с комплексно-сопряженными координатами, а середина хорды, определенная этими точками будет действительной точкой и она лежит на диагонали.
Составим уравнение диаметра
Пусть прямая 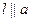 , и пересекает f в т.: М1 и М2
, и пересекает f в т.: М1 и М2
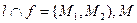 - середина М1М2 и
- середина М1М2 и
произвольная точка диаметра
Обозначим параметры, определяющие
т. М1 и М2 через t1 и t2
t1 и t2 – корни уравнения: 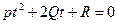 (1)
(1)
Пусть M(x,y), тогда 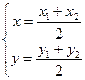
Но 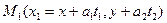

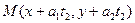
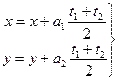
Эти равенства возможны  По т. Виета для уравнения (1):
По т. Виета для уравнения (1):
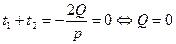
Верно и обратное: если 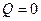 , то
, то 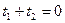
Таким образом, получим, что 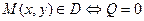
Запишем последнее равенство в координаты: 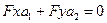 (2)
(2)
Если 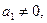 то разделив обе части последнего уравнения на а1 и учитывая, что
то разделив обе части последнего уравнения на а1 и учитывая, что
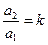 - угловой коэффициент а, получим:
- угловой коэффициент а, получим: 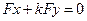
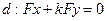 (3)
(3)
Покажем, что уравнение (3) задает прямую линию.
Запишем уравнение (2) в развернутом виде:
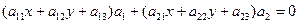
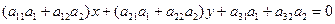
Полученное уравнение не выше 1ой степени; покажем, что это уравнение точно 1ой степени. Допустим противное:

P = 0
Получим противоречие (а – вектор асимптотического направления, следовательно, уравнение диаметра имеет 1ю степень и d является прямой линией)
Рассмотрим диаметры центральной и не центральной линии.
1). f - центральная линия, т.е. 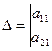
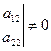
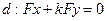
Вычислим условный коэффициент диаметра. Для этого запишем уравнение диаметра в развернутом виде:
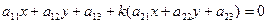
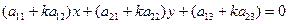
 (4)
(4)
Получим k’ – угловой коэффициент диаметра центральной линии. Направление задаваемое угловым коэффициентом k’ и k называют сопряженнными. Решая (4) относительно k, получим: 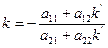
Из последнего уравнения заключаем, что если направление k сопряженно направлению k’, то и направление k’сопряженно направлению k. В силу этого свойства направления k и k’ называются взаимно сопряженными. Геометрически, это означает, что каждый из 2х сопряженных диаметров делит хорду, параллельную другому диаметру пополам. Из уравнения (3) видно, что любой диаметр центральной линии проходит через центр кривого, т.к. центр удовлетворяет уравнению: 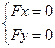
2). f - нецентральная линия, т.е. 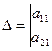
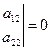 , или
, или 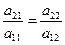
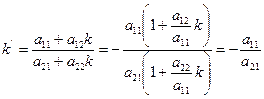
Таким образом, мы показали, что угловой коэффициент диаметра не зависит от углового коэффициента а, т.е. все диаметры нецентральной линии параллельны между собой.
Оси.
Df: Осью линии 2го порядка, называют диаметр, перпендикулярного своему сопряженному направлению.
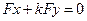 - ось
- ось 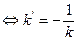
Подставим в последнее равенство k’, выраженное через k:
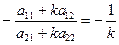
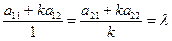


Система однородного линейного уравнения имеет ненулевое решение, что определитель этой системы равен нулю, т.е. 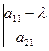
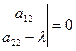 (5) –характерное уравнение линии 2го порядка.
(5) –характерное уравнение линии 2го порядка.
Подставим корни этого уравнения в предыдущую систему:
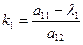
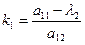
Получим 2 оси, которые задаются уравнениями:
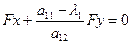
оси центральной линии
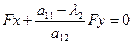
Если линия нецентральная, то угловой коэффициент нецентральной линии k’ равен:
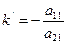 Но
Но 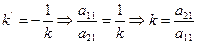
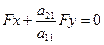
оси нецентральной линии
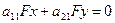
Дата публикования: 2015-07-22; Прочитано: 352 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
