Группы движений плоскости и ее подгруппы

Th1: Множеству движений плоскости образует группу.

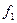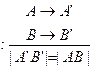1). Пусть движ. (1)

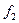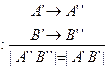Пусть движ. (2)

Тогда преобразование движений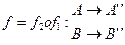

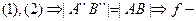движение

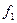
2). 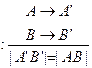(3)

Рассмотрим обратное произведение: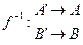

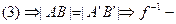движение

Из доказанных свойств 1 и 2 Þ множество движений является подгруппой всех преобразований плоскости Þ множество движений есть группа.

Th2: Множество всех точек движений 1^го рода образует группу, которая является подгруппой группы движений.

Доказательство:

Каждое движение 1^го рода сохраняет ориентацию плоскости, поэтому произведение движений 1^го рода и движения обратного движения 1^го рода, сохраняет ориентацию плоскости, т.е. является движением 1^го рода.

Th3: Множество параллельных переносов образует группу, которая является подгруппой группы движений 1^го рода.

Доказательство:

Пусть даны 2 параллельных переноса: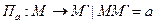

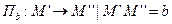
Рассмотрим произведения параллельных переносов: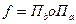

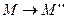
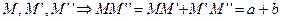. Значит f является параллельным переносом на вектор, равный сумме векторов a и b, т.е.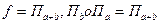

Пусть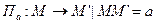

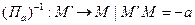
Следовательно, преобразование обратного переноса есть параллельный перенос

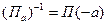- теорема доказана

Выберем на плоскости прямую 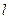и обозначим через а вектор, параллельный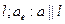

Рассмотрим множество всех векторов, параллельных фиксированных прямой 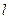. Параллельные переносы, определенные этими векторами, назовем параллельными переносами вдоль прямой .

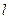Th4: Множество параллельных переносов вдоль фиксированной прямой образует группу, которая является подгруппой группы всех параллельных прямых.

Доказательство:

Пусть даны 2 пары параллельных переноса вдоль прямой 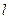: 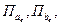и рассмотрим их произведение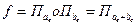

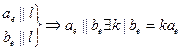
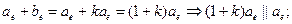но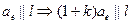

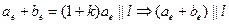
Пусть дан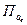

Рассмотрим обратное преобразование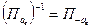

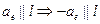
Параллельный перенос, обратный параллельному переносу вдоль l есть перенос того же вида.

Th5: Множество поворотов плоскости группы не образует, так как произведение 2^х поворотов с различными центрами может быть и не поворотом, а параллельным переносом.

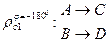
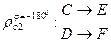
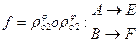
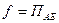
Но множество всех поворотов с фиксированным центром образует группу, которая является подгруппой группы движений 1^го рода, т.к.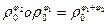

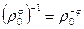
Если тождественное преобразование рассматривать как параллельный перенос на нулевой вектор или на нулевой угол как поворот, то образует группу, которая является подгруппой параллельного переноса. Доказанные Th позволяют построить таблицу строения группы движений.

Замечание: Множество движений 2^го рода группы не образует, т.к. произведение 2^х движений 2^го рода есть движение 1^го рода.

Лекция 23