 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Асимптоты. Df: Прямая называется асимптотой кривой, если при бесконечном уравнении от начала координат расстояние от точек кривой до прямой
|
|
Df: Прямая называется асимптотой кривой, если при бесконечном уравнении от начала координат расстояние от точек кривой до прямой, неограниченно уменьшается.
Tp: Прямая  является асимптотой гиперболы
является асимптотой гиперболы 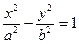
Доказательство:
Доказательство Tp проведем для ветви гиперболы, лежащей в ± четверти. Остальные ветви будут следовать из св. 10.
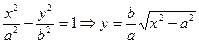
M(x,y) Î I четв
M(x,y) Î j
M1 = Ox Ù MM1 ^ Ox
M2 = e Ù MM1 ^ e
N = e Ù MM1
| M1M2 | = d = r (M,e)
| M1M2 | < | MN |; N (x,y)
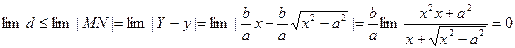 (3)
(3)
d 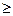 0 (4)
0 (4)
(3), (4) Þ lim d = 0
Df: точки пересечения гиперболы с осью на которой лежат фокусы называются вершинами гиперболы.
Расстояние между вершинами 2а, вершины имеют координаты:
A1(-a, 0), A2(a, 0); | A1A2 | = 2a (действительная ось)
B1(0, -b), B2(0, b); | B1B2 | = 2b (мнимая ось)
Все сказанное дает возможность построения.
Строится прямоугольник, центр которого совпадает с центром гиперболы, стороны которого проходят через т A1, A2, B1, B2 параллельно осям гиперболы, диагоналями этого прямоугольника являются асимптотами гиперболы.
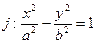
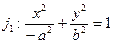
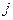 и
и 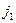 - взаимно сопряжены
- взаимно сопряжены
Df: если a = b т.е. мнимая ось равно действительной, то гипербола называется равнобочной
x2 – y2 = a2 – каноническое уравнение равнобочной гиперболы.
Df: 2 гиперболы, имеющие общие асимптоты и общие оси, но при этом действ. ось одной гиперболы (ось, на которой лежат фокуса) совпадает с мнимой осью другой называется сопряженными.
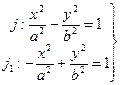 пара взаимно сопряженных гипербол
пара взаимно сопряженных гипербол
Лекция 14
Парабола: определение, каноническое уравнение, свойства.
Df: Параболой называется множество точек плоскости, для каждой из которых расстояние до данной ориентированной точки плоскости, называется фокусом, равно расстоянию до данной фиксированной прямой, называется директриссой.
d – директрисса, F Ï d, F- фокус
j = { M | | FM | = r (M, d) } Обозначение r (F, d) = p (1)
Составим каноническое уравнение параболы. Для этого введем на плоскости ДПСК R = { O, (i, j) }
(FN) ^ d
N = d Ç FN
O – середина [ NF ]
i NF
j | R – правый репер
" M (x, y) Î о Û | FM | = r (M, d) (2)
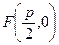
d: x = -p/2
Перепишем равенство (2) в виде:
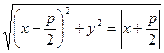 (3) – уравнение параболы
(3) – уравнение параболы
Т.к. обе части уравнения (3) неотрицательны, то возведя обе части уравнения в квадрат, получим уравнение равносильное исходному, т.е. получим уравнение:
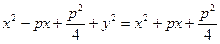
j: y2 = 2px (4) – каноническое уравнение параболы
Df: Отрезок, соединяющий фокус параболы с точкой, лежащей на параболе, называется фокальным радиусом параболы.
Выведем формулу для нахождения длины фокального радиуса.
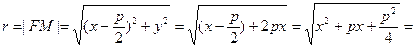
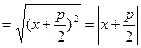 (5)
(5)
(4) 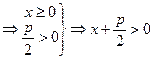 (6)
(6)
(5), (6) Þ 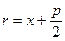
Дата публикования: 2015-07-22; Прочитано: 257 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
