Дисперсия среднего серии измерений

Пусть распределение случайной величины Х подчинено нормальному закону

.

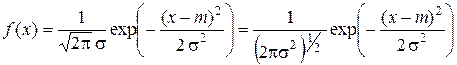Тогда вероятность совместного осуществления n независимых событий Х = x_i (i = 1, 2, …, n) равна

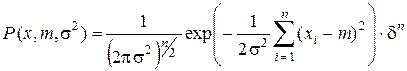(3.15)

и функция правдоподобия

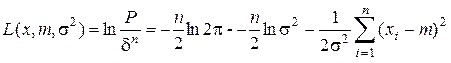. (3.16)

Продифференцируем (3.16) по m

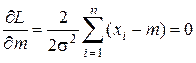. (3.17)

Поскольку 1/s² ¹ 0, то

.

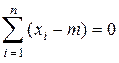Тогда оценка для математического ожидания равна

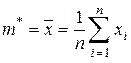, (3.18)

где 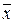— среднее арифметическое выборки (серии измерений). Отметим, что для выборочного среднего сохраняются все свойства математического ожидания. Например, если Z является нелинейной функцией n независимых случайных величин

Z = f (X ₁, X ₂, …, Х_n),

то ее выборочное среднее приближенно выражается формулой

.

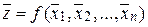Дифференцируя функцию правдоподобия (3.16) по s², получаем

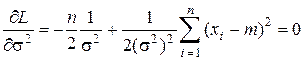, (3.19)

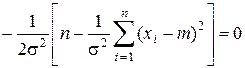. (3.20)

Поскольку 1/(2s²) ¹ 0, то

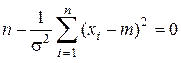, (3.21)

откуда находим оценку s ₁² для дисперсии случайной величины:

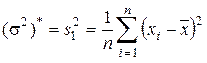. (3.22)

Метод максимального правдоподобия всегда приводит к состоятельным, хотя иногда и смещенным оценкам, имеющим наименьшую возможную дисперсию при неограниченном возрастании объема выборки. Так, выборочная дисперсия s ₁² оказывается смещенной оценкой генеральной дисперсии

. (3.23)

Для получения несмещенной оценки дисперсию s ₁² надо умножить на величину n /(n - 1)

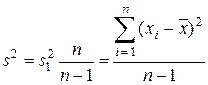. (3.24)

Уменьшение знаменателя в (3.24) на единицу непосредственно связано с тем, что величина 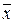, относительно которой берутся отклонения, сама зависит от элементов выборки. Каждая величина, зависящая от элементов выборки и входящая в формулу выборочной дисперсии, называется связью. Можно доказать, что знаменатель выборочной дисперсии всегда равен разности между объемом выборки n и числом связей l, наложенных на эту выборку. Эта разность

f = n – l (3.25)

называется числом степеней свободы выборки.

В практических вычислениях для выборочной дисперсии s ² часто более удобна следующая формула, получаемая из (3.24) путем арифметических преобразований:

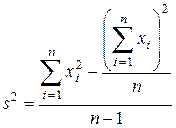. (3.26)

Итак, для нормально распределенной случайной величины получают по выборке следующие оценки генеральных параметров распределения: среднее арифметическое 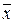для математического ожидания m и выборочную дисперсию s ² для генеральной дисперсии s².

Определим дисперсию среднего арифметического через дисперсию единичного наблюдения, воспользовавшись свойствами дисперсии. Если Х ₁, Х ₂, …, Х_n — независимые случайные величины, а ₁, а ₂, …, а_n — неслучайные величины, а функция Z равна

Z = а ₁ X ₁ + а ₂ X ₂ + … + а_nX_n , (3.27)

то дисперсия Z определяется следующим образом:

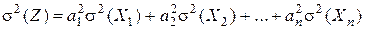. (3.28)

Пусть в результате одной серии опытов получена выборка х ₁, х ₂, …, х_n. Если провести несколько серий подобных наблюдений, то в общем случае будут получены другие совокупности значений случайной величины Х: х ₁^', х ₂^', …, х_n ^'; х ₁^'', х ₂^'', …, х_n ^'' и т.д. Поэтому значения х ₁, х ₂, …, х_n в серии из n наблюдений можно рассматривать как случайные величины с некоторыми дисперсиями s²(х ₁), s²(х ₂), …, s²(х_n). Поскольку эти случайные величины возникают при измерении одной и той же случайной величины Х, то дисперсии их естественно считать одинаковыми:

s²(х ₁) = s²(х ₂) = … = s²(х_n) = s². (3.29)

Применим теперь (3.28) для случая, когда Z является средним арифметическим (в этом случае а ₁ = а ₂ = … = а_n = 1/ n):

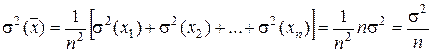. (3.30)

Из (3.30) следует, что дисперсия среднего в n раз меньше дисперсии единичного измерения, поэтому для стандартного отклонения

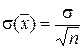. (3.31)

Если принять 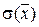в качестве меры случайной ошибки среднего выборки, то увеличение числа параллельных определений одной и той же величины снижает величину случайной ошибки. Это свойство случайной величины используют на практике для повышения точности результатов измерений.

Так как свойства генеральных дисперсий сохраняются и для их оценок — выборочных дисперсий, то

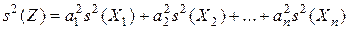, (3.32)

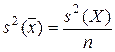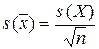, , (3.33)

где s ² — выборочные дисперсии, s — выборочное отклонение.

ЛЕКЦИЯ 4

Доверительные интервалы и доверительная вероятность, уровень значимости. Проверка статистических гипотез, критерии значимости, ошибки первого и второго рода. Построение доверительного интервала для математического ожидания непосредственно измеряемой величины. Распределение Стъюдента.