Косвенных измерений

В самом общем виде пример косвенных измерений формулируется следующим образом: имеется известная функция нескольких аргументов

Z = f (X ₁, X ₂, …, Х_k),

причем на опыте непосредственно измеряются случайные величины X ₁, X ₂, …, Х_k. При строгом статистическом анализе случайной ошибки Z необходимо найти закон распределения функции по известным законам распределения аргументов, что связано с большими вычислительными трудностями. Из-за этого строгая оценка ошибки косвенных измерений трудно выполнима и практически нецелесообразна. Поэтому используются упрощенные подходы, значительно облегчающие расчеты и вместе с тем дающие удовлетворительные для практических целей результаты.

Рассмотрим вначале случай, когда Z является известной функцией только одного параметра X: Z = f (X). Введем допущение о том, что в небольших интервалах изменения нормально распределенного аргумента функция этого аргумента также подчиняется нормальному закону распределения. Пусть х ₁, х ₂, …, х_n — результаты n измерений величины Х. Для каждого из х_i можно найти соответствующее значение z_i, затем вычислить среднее 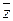и выборочную дисперсию s ²(Z) с числом степеней свободы f = n – 1. Тогда согласно изложенному в предыдущем разделе имеем

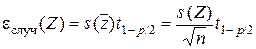. (5.1)

При учете только случайной ошибки результат измерений функции следует записать так:

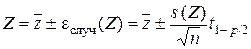. (5.2)

Если f (x) является достаточно сложной функцией и каждый раз вычисление величины z_i по значению х_i трудоемко, то можно определить сначала величины 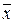и s (X), а затем пересчитать их в соответствующие величины 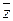и s (Z) при помощи приближенных формул:

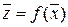, (5.3)

. (5.4)

Для случая, когда Z является извеcтной функцией нескольких аргументов, используем следующие допущения:

1) Случайные величины X ₁, X ₂, …, Х_k независимы.

2) В небольших интервалах изменения аргументов функция Z распределена нормально.

3) Выборочная дисперсия величины 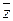равна соответствующей генеральной

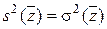. (5.5)

Оценка случайной ошибки функции проводится в следующем порядке. Находим среднее функции:

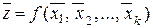, (5.6)

где — средние по выборкам соответствующих аргументов. Затем по закону накопления ошибок оцениваем выборочную дисперсию

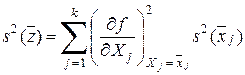. (5.7)

Тогда величина случайной ошибки функции определяется следующим образом:

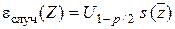, (5.8)

где U _{1- p /2} — квантиль стандартного нормального распределения (приложение 2), равный 1,96 для уровня значимости р = 0,05.

При учете только случайной ошибки для доверительной вероятности b = 0,95 результат измерений функции нескольких аргументов следует записать так:

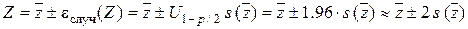. (5.9)

Случайную ошибку косвенных измерений можно оценить также, воспользовавшись формулами расчета погрешностей функций приближенных аргументов (лекция 1) для случая, когда погрешности аргументов независимы и случайны:

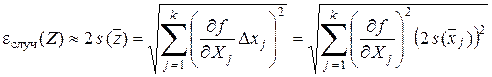, (5.10)

при этом в качестве абсолютной погрешности аргументов следует использовать удвоенное значение среднеквадратичных отклонений их средних

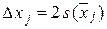. (5.11)

В общем случае при представлении результатов измерений следует учитывать не только случайную, но и систематическую ошибку методики или прибора. Предполагая, что эти два типа ошибки взаимонезависимы, суммарная ошибка измерений равна:

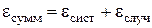. (5.12)

Систематические ошибки являются величинами, не зависящими от числа измерений, и определяются спецификой используемой аппаратуры и методом измерений. Так, например, с помощью ртутного термометра нельзя измерить температуру с точностью, большей 0,01 ^оС (редко 0,005 ^оС); значение эталонного сопротиления может быть известно с точностью 0,1% или 0,01%; и т. д. Если и источники, и величины систематических ошибок определены, то их влияние на окончательный результат косвенных измерений для функции нескольких аргументов можно оценить как предельную абсолютную погрешность по формуле (лекция 1)

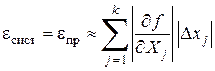. (5.13)

Величина систематической ошибки ограничивает число верных значащих цифр при представлении результатов эксперимента. С учетом систематической ошибки результат любого измерения следует записывать следующим образом:

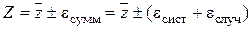. (5.14)

5.2. Оценка дисперсии нормально распределенной

случайной величины.

Дисперсию генеральной совокупности s² нормальной распределенной случайной величины можно оценить, если известно распределение ее оценки — выборочной дисперсии s ². Распределение выборочной дисперсии можно получить при помощи распределения Пирсона или c²-распределения.

Пусть имеется выборка n независимых наблюдений х ₁, х ₂, …, х_n над нормально распределенной случайной величиной. Можно показать, что сумма

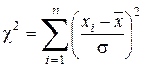(5.15)

имеет распределение с f = n – 1 степенями свободы. Плотность c² распределения зависит только от числа степеней свободы f:

j (c²) 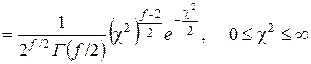, (5.16)

где Г (f ) — гамма-функция. На рис. 15 приведены кривые плотности вероятности c² распределения при некоторых значениях f. Кривые асимметричны, степень асимметрии уменьшается с увеличением f.

Рис. 15. Плотность c²-распределения.

При доверительной вероятности b = 1 – р двусторонняя доверительная оценка для c² имеет вид

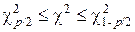, (5.17)

односторонние оценки имеют вид

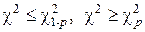. (5.18)

Квантили 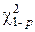при различных р и f приведены в приложении 4.

Поскольку выборочная дисперсия определяется по формуле

,

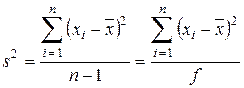то с учетом (5.15) имеем:

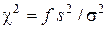. (5.19)

Подставляя (5.19) в (5.17) и решая полученное неравенство относительно s², получим доверительные двусторонние границы для генеральной дисперсии:

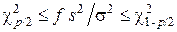, (5.20)

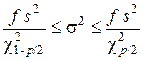. (5.21)

Аналогично получаются односторонние доверительные оценки:

. (5.22)

С ростом числа степеней свободы асимметрия кривых c²-распре-деления уменьшается, соответственно уменьшается и асимметрия доверительных границ. Можно показать, что при n ³ 30 выборочный стандарт s распределен приближенно нормально с математическим ожиданием m_s = s и среднеквадратичной ошибкой

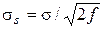. (5.23)

Неизвестный генеральный стандарт в (5.23) при n ³ 30 заменяют выборочным

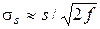. (5.24)

Тогда по уравнению (4.8) (лекция 4) доверительные границы для генерального стандарта определяются неравенством

. (5.25)