Понятие об оценках параметров генерального распределения

Явление статистической устойчивости результатов наблюдений имеет место лишь при большом (в пределе — бесконечно большом) числе измерений. В подавляющем же числе экспериментов исследователю приходится иметь дело лишь с ограниченным, обычно небольшим, числом наблюдений. В силу закона случая какие-то величины, определенные по малому числу наблюдений, в общем случае могут не совпадать с теми же величинами, вычисленными по большому числу наблюдений, выполненных в тех же условиях. Поэтому в математической статистике вводят понятие абстрактной генеральной совокупности, состоящей из всех допустимых значений случайной величины, и выборки, представляющей собой совокупность ограниченного числа значений, полученных в результате опытов. В соответствии с этим различают выборочные характеристики случайной величины, найденные по ограниченному числу наблюдений и зависящие от этого числа, и соответствующие им характеристики генеральной совокупности. При этом выборочные характеристики рассматриваются как оценки соответствующих характеристик генеральной совокупности.

Выборка называется репрезентативной (представительной), если она дает достаточное представление об особенностях генеральной совокупности. Однако из случайного характера выборок следует, что любое суждение о генеральной совокупности само случайно. Предположим, что в результате эксперимента получена выборка из х ₁, х ₂, …, х_n значений случайной величины Х. Обозначим через n_x число выборочных значений, расположенных левее х — некоторой точки числовой оси Х. Отношение (n_x / n) есть частота появления значений Х, меньших х, и является функцией от х. Эта функция, получаемая по выборке, называется эмпирической, или выборочной функцией распределения (в отличие от распределения генеральной совокупности) и обозначается как

F_n (x) = n_x / n. (3.1)

Можно доказать, что с вероятностью, равной 1, при n ®¥ максимальная разность между функциями распределения случайной величины F_n (x) и F (x) стремится к нулю. На практике это означает, что при достаточно большой выборке функцию распределения генеральной совокупности приближенно можно заменять выборочной функцией распределения. Пусть х ₁ < х ₂ < … < х_n (упорядоченная по величине выборка, или вариационный ряд). Все элементы выборки имеют одинаковую вероятность, равную 1/ n. Поэтому

F_n (x) = 0 при x < x ₁,

F_n (x) = k / n при x_k £ x < x_{k +1}, где k = 1, 2, …, n – 1,

F_n (x) = 1 при x ³ x_n.

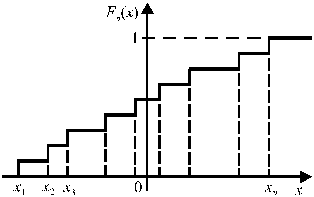График F_n (x) представлен на рис. 9. Все элементы выборки оказываются точками разрыва этой функции. В точке разрыва х = х_k функция скачком переходит от значения (k – 1)/ n к значению k / n, которое и удерживает в следующем интервале.

Рис. 9. Выборочная функция распределения.

При обработке выборок обычно используют метод «сгруппированных данных»: выборка объема n преобразуется в статистический ряд. Весь диапазон значений случайной величины от х _min до x _max делится на k равных интервалов ( j = 1, 2, …, k). Число интервалов можно выбирать произвольно или по эмпирическим формулам, например:

(3.2)

с округлением до ближайшего целого. Длина интервала равна

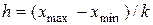. (3.3)

Число элементов выборки, попавших в j -интервал, обозначим через n_j. Величина

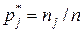(3.4)

определяет относительную частоту попадания случайной величины в j -интервал. Все точки, попавшие в j -интервал, относят к его середине:

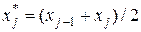. (3.5)

Статистический ряд записывается в виде табл. 1.

Таблица 1

Статистический ряд.

Интервал	Длина интервала	Середина интервала	Число точек в интервале	Относительная частота
	(х min, x 1)	x 1*	n 1	p 1*
	(х 1, x 2)	x 2*	n 2	p 2*
…	…	…	…	…
k	(хk -1, x max)	xk *	nk	pk *
S			n

График, построенный по данным табл. 1, называется гистограммой эмпирического, или выборочного, распределения (рис. 10). На рис. 11 приведен график функции F_n (x), построенный по сгруппированным данным.

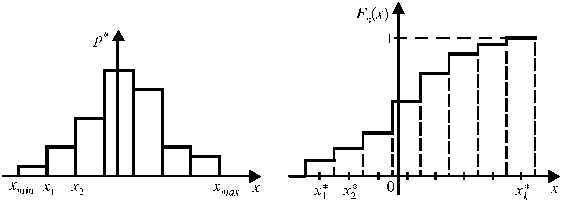
Рис. 10. Гистограмма распределения. Рис. 11. График функции F _n(x),

построенный по сгруппированным

данным.

При обработке результатов наблюдений обычно не удается получить эмпирическую функцию распределения. Однако даже простейший анализ условий опыта позволяет с достаточной уверенностью определять тип неизвестной функции распределения. Окончательное уточнение неизвестной функции распределения сводится к определению некоторых числовых параметров распределения. По выборкам могут быть рассчитаны выборочные статистические характеристики (выборочное среднее, дисперсия и т.д.), которые являются оценками соответствующих генеральных параметров.

Оценка а ^*(х ₁, х ₂, …, х_n) называется состоятельной, если с увеличением объема выборки n она стремится (по вероятности) к оцениваемому параметру а. Эмпирические (выборочные) моменты являются состоятельными оценками теоретических моментов.

Оценка а ^*(х ₁, х ₂, …, х_n) называется несмещенной, если ее математическое ожидание при любом объеме выборки равно оцениваемому параметру а, т. е. М [ а ^*] = а.

Важной характеристикой оценок генеральных параметров является также их эффективность, которая для различных несмещенных оценок одного и того же параметра при фиксированном объеме выборок обратно пропорциональна дисперсиям этих оценок.