ЛЕКЦИЯ 2. Числовые характеристики случайной величины. Свойства математического ожидания и дисперсии

Числовые характеристики случайной величины. Свойства математического ожидания и дисперсии. Нормированная случайная величина. Квантили. Нормальное и стандартное распределения случайной величины. Функция Лапласа. Задача об абсолютном отклонении.

2.1. Числовые характеристики случайной величины.

Свойства математического ожидания и дисперсии.

Нормированная случайная величина.

Вместо полного определения случайной величины в виде законов распределения вероятностей в прикладных задачах ее часто определяют при помощи числовых характеристик — чисел (вещественных), выражающих характерные особенности случайной величины, называемых моментами случайной величины.

Наиболее часто в приложениях математической статистики используют математическое ожидание (характеристику положения значений случайной величины на числовой оси) и дисперсию (или среднее квадратичное отклонение), определяющую характер разброса значений случайной величины.

Математическое ожидание (генеральное среднее) случайной величины (начальный момент первого порядка) принято обозначать М [ Х ], m_x или m. Оно определяется для дискретной и непрерывной случайной величины соответственно как

m = M [ X ] = 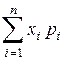, (2.1)

m_х = M [ X ] = 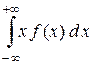. (2.2)

Для случайных величин математическое ожидание является теоретической величиной, к которой приближается среднее значение 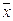случайной величины Х при большом количестве испытаний.

Свойства математического ожидания:

1. Если с — постоянное число (неслучайная величина), то

М [ c ] = c, (2.3)

М [ cХ ] = c М [ Х ]. (2.4)

2. Математическое ожидание суммы случайных величин равно сумме математических ожиданий этих случайных величин:

М [ Х ₁ + Х ₂ + …+ Х_n ] = М [ Х ₁] + М [ Х ₂] + … + М [ Х_n ]. (2.5)

3. Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей:

М [ Х ₁× Х ₂× Х ₃×…× Х_n ] = М [ Х ₁]× М [ Х ₂]× М [ Х ₃]×…× М [ Х_n ]. (2.6)

Случайные величины называются независимыми, если каждая из них имеет самостоятельное распределение, не зависящее от возможных значений других величин.

4. Если случайная величина Z является некоторой нелинейной функцией n независимых случайных величин

Z = f (X ₁, X ₂, …, Х_n),

которая мало меняется в небольших интервалах изменения аргументов, то

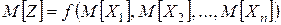. (2.7)

Дисперсией (вторым центральным моментом) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т. е.

D [ X ] = M [(X – m_x)²]. (2.8)

Для дискретной и непрерывной случайных величин дисперсия определяется следующим образом соответственно:

D [ X ] = 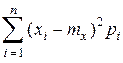, (2.9)

D [ X ] = 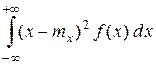. (2.10)

Другие обозначения для дисперсии: D _x, s _x ², s²(X).

Дисперсия играет важную роль при статистических расчетах и является мерой рассеяния значений х около их математического ожидания. Корень квадратный из второго центрального момента называется средним квадратичным отклонением (стандартным отклонением, или стандартом):

s _x = s = . (2.11)

Свойства дисперсии:

1. Если с — постоянное число (неслучайная величина), то

s²(c) = 0, (2.12)

s²(cХ) = с ² s²(Х). (2.13)

2. Дисперсия случайной величины равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания:

s²(Х) = М [ 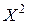] — 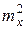. (2.14)

3. Дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин:

s²(Х ₁ + Х ₂ +…+ Х_n) = s²(Х ₁) + s²(Х ₂) + … +s²(Х_n). (2.15)

Выражение (2.15) называют законом сложения дисперсий. Следует отметить, что закон сложения справедлив для дисперсий случайных величин (s²), а не среднеквадратичных отклонений (s).

4. Если случайная величина Z является нелинейной функцией n независимых случайных величин

Z = f (X ₁, X ₂, …, Х_n),

которая мало меняется в небольших интервалах изменения аргументов, то ее дисперсия приближенно равна

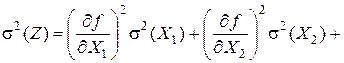
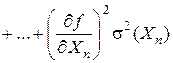. (2.16)

Выражение (2.16) называют законом накопления ошибок, и он часто используется в теории ошибок для определения случайной ошибки функции по значениям случайных ошибок аргументов.

Третий центральный момент, разделенный на s _x ³, называется коэффициентом асимметрии плотности распределения:

g = 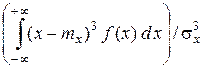. (2.17)

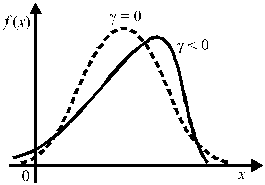На рис. 5 приведены примеры плотностей распределения с одинаковыми математическим ожиданием и дисперсией, но с разными коэффициентами асимметрии.

Рис. 5. Плотности распределения с нулевым

и ненулевым коэффициентами асимметрии.

Если у случайной величины Х существуют первый и второй моменты, то можно построить нормированную случайную величину

, (2.18)

для которой

М [ X ₀] = 0, D [ X ₀] = 1. (2.19)

Докажем, что для нормированной случайной величины справедливы утверждения (2.19):

,

.

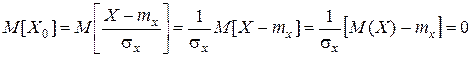Существуют следующие соотношения между функциями распределения, соответствующими нормированной Х ₀ и ненормированной Х величинам:

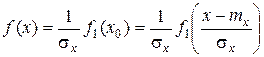, (2.20)

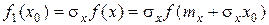, (2.21)

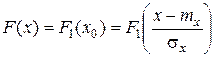, (2.22)

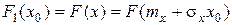. (2.23)

Рассмотренные выше моменты являются общими (интегральными) характеристиками распределения случайной величины. Вторая группа параметров характеризует отдельные значения функции распределения. К ним относятся квантили. Квантилем х _b распределения случайной величины Х с функцией распределения F (x) называется решение уравнения F (x _b) = b, т. е. такое значение случайной величины, что Р (Х £ x _b) = b. Наиболее важное значение имеет квантиль х _1/2, называемый медианой распределения (рис. 6).

Рис. 6. Медиана распределения.

Ордината медианы пополам рассекает площадь между кривой плотности вероятности и осью абсцисс. Если распределение симметрично, то х _1/2 = m_x.

2.2. Нормальное и стандартное распределения

случайной величины. Функция Лапласа.

Задача об абсолютном отклонении.

Непрерывная случайная величина Х называется распределенной по нормальному закону, если ее плотность распределения имеет вид

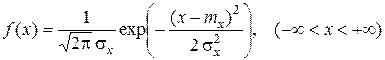, (2.24)

где m_x и 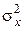— математическое ожидание и дисперсия случайной величины Х.

Функция распределения равна

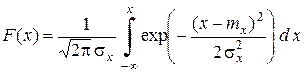. (2.25)

Нормальное распределение наиболее часто встречается на практике и теоретически наиболее полно разработано. Множество событий происходит случайно вследствие воздействия на них большого числа независимых (или слабо зависимых) возмущений, и у таких явлений закон распределения близок к нормальному. Установлено, что нормальное распределение содержит минимум информации о случайной величине по сравнению с любыми распределениями с той же дисперсией. Следовательно, замена некоторого распределения эквивалентным нормальным не может привести к переоценке точности наблюдений, что широко используется на практике.

График плотности нормального распределения называется нормальной кривой, или кривой Гаусса (рис. 7).

Рис. 7. Кривая Гаусса. Рис. 8. График функции F ₀(x)

стандартного распределения.

Нормальное распределение нормированной случайной величины называется стандартным. Его функция распределения имеет вид

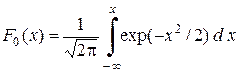, (2.26)

а график этой функции представлен на рис. 8.

Вероятность того, что значения нормированной случайной величины будут лежать в интервале от х ₀₁ до х ₀₂, равна

Р (х ₀₁ £ Х ₀ £ х ₀₂) = F ₀(х ₀₂) – F ₀(х ₀₁). (2.27)

Функция

Ф (Х) = F ₀(х) – ½ (2.28)

называется функцией Лапласа

Ф (Х) = F ₀(х) – ½ = F ₀(х) – F ₀(0) = 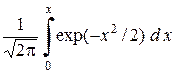. (2.29)

Значения функции Лапласа табулированы (приложение 1). Так как она является нечетной функцией, т. е. Ф (- х) = - Ф (х), то таблицы значений Ф (х) составлены лишь для х > 0.

Для нормированной случайной величины с учетом (2.27) и (2.28) имеем:

Р (х ₀₁ £ Х ₀ £ х ₀₂) = F ₀(х ₀₂) – F ₀(х ₀₁) =

= Ф (х ₀₂) + ½ - Ф (х ₀₁) - ½ = Ф (х ₀₂) - Ф (х ₀₁). (2.30)

Тогда в общем случае

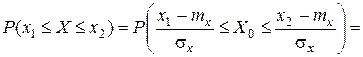
. (2.31)

Во многих практических задачах х ₁ и х ₂ симметричны относительно математического ожидания, в частности в задаче об абсолютном отклонении. Абсолютным отклонением является величина

. (2.32)

Требуется найти вероятность того, что абсолютное отклонение случайной величины не превзойдет некоторого заданного числа e:

P (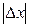 £ e) = P (m_x - e £ X £ m_x + e). (2.33)

В частности, для нормированной случайной величины

P (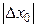 £ e) = P (-e £ X ₀ £ +e) = Ф (e) – Ф (-e) = 2 Ф (e). (2.34)

Тогда для нормально распределенной случайной величины с параметрами m_x и s _х справедливо

P (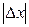 £ e) = 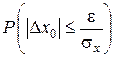= 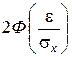. (2.35)

Обозначив e/s _х = k, из (2.35) получаем

P (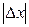 £ k s _х) = 2 Ф (k), (2.36)

откуда

P (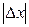 £ s _х) = 2 Ф (1) = 0.6826,

P (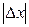 £ 2s _х) = 2 Ф (2) = 0.9544,

P (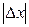 £ 3s _х) = 2 Ф (3) = 0.9973.

Таким образом, отклонения больше, чем утроенный стандарт (утроенное стандартное отклонение), практически невозможны. На практике часто величины 2s_х (или 3s_х ) считают максимально допустимой ошибкой и отбрасывают результаты измерений, для которых величина отклонения превышает это значение, как содержащие грубые ошибки.

Нормальное распределение обладает также свойством линейности: если независимые случайные величины Х ₁ и Х ₂ имеют нормальные распределения, то для произвольных чисел a и b величина

Y = a X ₁ + b X ₂

также имеет нормальное распределение, причем из свойств математического ожидания и дисперсии следует, что

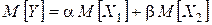, (2.37)

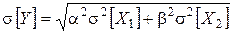. (2.38)