ЛЕКЦИЯ 1. Классификация ошибок измерений.

Случайные величины. Классификация ошибок измерений. Абсолютная и относительная погрешность. Прямые и косвенные измерения. Оценка погрешностей функций приближенных аргументов. Распределение случайных величин. Функция распределения и плотность распределения.

1.1. Случайные величины.

Классификация ошибок измерений.

Абсолютная и относительная погрешность.

Под случайной величиной понимают величину, принимающую в результате испытания значение, которое принципиально нельзя предсказать, исходя из условий опыта. Случайная величина обладает целым набором допустимых значений, но в результате каждого отдельного опыта принимает лишь какое-то одно из них. В отличие от неслучайных величин, изменяющих свое значение только при изменении условий опыта, случайная величина может принимать различные значения даже при неизменном комплексе основных факторов.

Различают дискретные и непрерывные случайные величины. Возможные значения дискретных величин можно заранее перечислить. Значения непрерывной случайной величины не могут быть заранее перечислены, они заполняют собой некоторый интервал. Набор допустимых значений сам по себе слабо характеризует случайную величину. Чтобы ее полностью охарактеризовать, необходимо не только указать, какие значения она может принимать, но и как часто.

Каждый результат измерения — случайная величина. Отклонение результата реального измерения от истинного значения величины называется ошибкой измерения. («Ошибка» в научном смысле означает неизбежную погрешность, которая сопутствует всем измерениям). Ни одну физическую величину (длину, время, температуру и т.д.) невозможно измерить с полной определенностью. Лучшее, на что можно рассчитывать, — это свести ошибки к возможному минимуму и надежно рассчитать их величины.

Различают ошибки измерений трех видов:

1. Грубые ошибки возникают вследствие нарушения основных условий измерения. Результат, содержащий грубую ошибку, резко отличается по величине от остальных измерений, на чем основаны некоторые критерии исключения грубых ошибок.

2. Систематические ошибки постоянны во всей серии измерений или изменяются по определенному закону. Выявление их требует специальных исследований, их всегда стремятся свести к минимуму, а при необходимости они обычно учитываются введением соответствующих поправок в результаты измерения.

3. Случайные ошибки — ошибки измерения, остающиеся после устранения всех выявленных грубых и систематических ошибок. Они вызываются большим количеством таких факторов, эффекты действия которых столь незначительны, что их нельзя выделить в отдельности (при данном уровне техники измерения). При этом распределение случайных ошибок обычно симметрично относительно нуля: ошибки, противоположные по знаку, но равные по абсолютной величине, встречаются довольно часто.

Корректный способ представления результатов любого измерения состоит в том, что экспериментатор указывает свою наилучшую оценку измеряемой величины и интервал, в котором, как он уверен, она лежит. Чтобы охарактеризовать отклонение приближенного значения некоторой величины от ее истинного значения, вводят понятия абсолютной и относительной погрешностей, отвлекаясь от конкретного источника погрешностей.

Пусть А — точное значение исследуемой величины, а — ее наилучшая экспериментальная оценка (обычно среднее арифметическое серии измерений). Под абсолютной ошибкой (или погрешностью) величины а понимают абсолютное значение разности между этими значениями:

e = ½ А – а ½ = ½D а ½, (1.1)

или

А = а ± e. (1.2)

Предельная абсолютная погрешность определяется как

e_пр. ³ ½ А – а ½, (1.3)

или

e_пр. ³ e, (1.4)

при этом

(а + e_пр.) ³ А и А ³ (а - e_пр.), (1.5)

т. е. истинное значение искомой величины заведомо лежит в пределах

а - e_пр. £ А £ а + e_пр.. (1.6)

Для характеристики относительной точности измерений, зависящей от значения измеряемой величины, вводится относительная погрешность:

, (1.7)

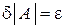. (1.8)

По аналогии с абсолютной погрешностью вводится также понятие предельной относительной погрешности:

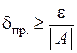, (1.9)

или

. (1.10)

Тогда

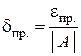, (1.11)

или

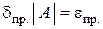. (1.12)

В вышеприведенные формулы входит неизвестная величина А, что делает невозможным численное определение погрешности. Практически поступают следующим образом: так как в большинстве случаев абсолютная погрешность много меньше самой измеряемой величины, т. е. e << 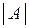, e << 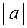или А» а, то для таких достаточно точных измерений можно записать:

и .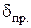

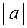
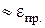Тогда с учетом определений абсолютной и относительной погрешностей получаем

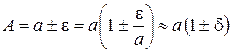или 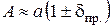. (1.13)

Относительная погрешность в отличие от абсолютной является величиной безразмерной и для большинства измерений представляет собой малое число, поэтому ее часто умножают на 100 и приводят в процентах.

1.2. Оценка погрешностей функций

приближенных аргументов.

Измерения делят на прямые и косвенные. В первом случае непосредственно измеряется определяемая величина, при косвенных измерениях она задается некоторой функцией от непосредственно измеряемых величин. Подавляющее большинство физико-химических свойств веществ и параметров процессов определяются в результате косвенных измерений, погрешность которых зависит от погрешностей непосредственно измеряемых величин, использованных в расчетах.

Предположим, что некоторые величины X ₁, X ₂, …, Х_n измерены с абсолютными погрешностями D х ₁, D х ₂, …, D х_n и что измеренные значения используются для вычисления функции

Z = f (X ₁, X ₂, …, Х_n). (1.14)

Очевидно, что погрешности приближенных аргументов должны привести к погрешности в значении искомой функции, что можно записать в следующем виде:

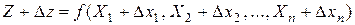, (1.15)

где D z — абсолютная погрешность функции Z.

Разложим правую часть равенства (1.15) в ряд Тейлора:

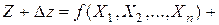
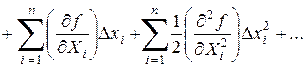. (1.16)

Если предположить, что измерения достаточно точны, так что величины D х_i малы по сравнению со значениями аргументов X_i, то в выражении (1.16) можно отбросить все члены, содержащие абсолютные погрешности аргументов во второй и высшей степенях. Тогда

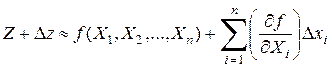, (1.17)

откуда с учетом (1.14) получаем

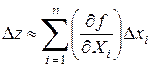. (1.18)

Выражение для предельной абсолютной погрешности функции n переменных запишется в следущем виде:

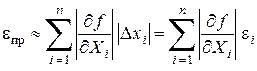, (1.19)

т.е. предельная абсолютная погрешность функции независимых переменных равна сумме частных производных этой функции, умноженных на соответствующие абсолютные погрешности аргументов. В практических расчетах значения частных производных берутся в точках, соответствующих измеренным значениям х_i или средним арифметическим 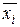, если проводились серии измерений.

В математической статистике также доказывается, что если абсолютные погрешности аргументов независимы и случайны, то наилучшей оценкой погрешности функции (1.14) будет квадратичная сумма ее частных производных, умноженных на соответствующие погрешности аргументов:

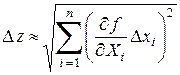. (1.20)

Формулы (1.19) и (1.20) являются основными при практических расчетах. Из них можно вывести формулы для расчетов погрешностей косвенных измерений для некоторых частных случаев, использование которых на практике бывает более удобным:

1. Измеренная величина умножается на точное число. Если величина X измерена с погрешностью D х и используется для вычисления

Z = BX,

в котором В — точное число, то абсолютная погрешность в Z равна

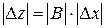.(1.21)

2. Погрешность в суммах и разностях. Если величины X ₁, X ₂, …, Х_n измерены с малыми погрешностями D х ₁, D х ₂, …, D х_n и измеренные значения используются для вычисления функции

Z = (X ₁ + … + Х_m) – (Х_k + …+ Х_n),

а погрешности аргументов независимы и случайны, то погрешность в Z равна квадратичной сумме исходных погрешностей:

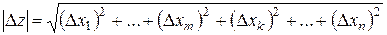; (1.22)

в любом случае она никогда не больше, чем их обычная сумма

. (1.23)

3. Погрешности в произведениях и частных. Если величины X ₁, X ₂, …, Х_n измерены с малыми погрешностями D х ₁, D х ₂, …, D х_n и измеренные значения используются для вычисления функции

,

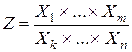а погрешности аргументов независимы и случайны, то относительная погрешность в Z равна квадратичной сумме исходных относительных погрешностей:

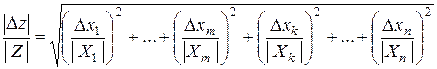; (1.24)

в любом случае она никогда не больше, чем их обычная сумма

. (1.25)

4. Погрешность в произвольной функции одной переменной. Если величина X измерена с погрешностью D х и используется для вычисления функции Z = f (X), то абсолютная погрешность в Z равна

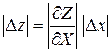. (1.26)

5. Погрешность в степенной функции. Если величина X измерена с погрешностью D х и используется для вычисления степенной функции 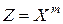(где m — фиксированное известное число), относительная погрешность в Z в 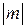раз больше, чем в Х:

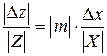. (1.27)

Пользуясь формулами (1.21) - (1.27), можно справиться практически с любой задачей вычисления ошибок в случае косвенных измерений. Любой расчет может быть представлен как последовательность определенных шагов, каждый из которых включает один из следующих видов операций: 1) нахождение сумм и разностей, 2) расчет произведений и частных, 3) вычисление функции одного переменного (данный метод называют «шаг за шагом»). Однако в случае когда выражение для вычисления функции Z включает одну и ту же величину более чем один раз (например, дважды Х ₁), то некоторые из ошибок могут взаимно компенсироваться и в результате расчет ошибки методом «шаг за шагом» может привести к переоценке конечной погрешности. Поэтому в подобных случаях рекомендуется пользоваться общими формулами (1.19) и (1.20).

1.3. Распределение случайных величин. Функция распределения

и плотность распределения случайной величины.

Пусть дискретная физическая величина Х может принимать в результате опыта значения х ₁, х ₂, …, х_n. Отношение числа опытов m_i, в результате которых величина Х принимает значение х_i, к общему числу проведенных опытов n называется частотой появления события Х = х_i. Частота (m_i / n) является случайной величиной и меняется в зависимости от количества проведенных опытов. Однако при большом количестве опытов (в пределе n ® ¥) она стабилизируется около некоторого значения р_i, называемого вероятностью события Х = х_i (статистическое определение):

р_i = Р (Х = х_i)» (m_i / n). (1.28)

Очевидно, что сумма вероятностей реализации всех возможных значений случайной величины равна единице:

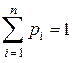. (1.29)

Дискретную случайную величину можно полностью задать вероятностным рядом, указав вероятность р_i для каждого значения х_i:

х 1	х 2	х 3	…	хn
р 1	р 2	р 3	…	рn

Законом распределения случайной величины называют любое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Вероятностный ряд является одним из видов законов распределения случайной величины.

Распределение непрерывной случайной величины нельзя задать вероятностным рядом, поскольку число значений, которое она может принимать, так велико, что для большинства из них вероятность принять эти значения равна нулю. Поэтому для непрерывных физических величин изучается вероятность того, что в результате опыта значение случайной величины попадет в некоторый интервал. Удобно пользоваться вероятностью события Х £ х, где х — произвольное действительное число. Эта вероятность

Р (Х £ х) = F (x) (1.30)

является функцией от х и называется функцией распределения (предельной функцией распределения, функцией распределения генеральной совокупности) случайной величины. В виде функции распределения можно задать распределение как непрерывной, так и дискретной случаной величины (рис. 2 и 3). F (x) является неубывающей функцией, т.е. если х ₁ £ х ₂, то F (х ₁) £ F (х ₂) (рис. 3).

Рис. 2. Функция распределения Рис. 3. Функция распределения

дискретной случайной величины. непрерывной случайной величины.

Ордината кривой F (x), соответствующая точке х_i, представляет собой вероятность того, что случайная величина Х при испытании окажется £ х_i. Тогда вероятность того, что значения случайной величины будут лежать в интервале от х ₁ до х ₂, равна

Р (х ₁ £ Х £ х ₂) = F (х ₂) - F (х ₁). (1.31)

Значения F (х) при предельных значениях аргумента равны: F (-¥) = 0, F (+¥) = 1. Следует отметить, что функция распределения дискретной случайной величины всегда есть разрывная функция. Скачки происходят в точках, соответствующих возможным значениям этой величины, и равны вероятностям этих значений (рис. 2).

Для непрерывной случайной величины наиболее часто используется производная функции распределения — плотность распределения случайной величины Х.

Если F (х) непрерывна и дифференцируема, то

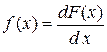. (1.32)

Задание f (x) также полностью определяет случайную величину. Плотность распреределения является неотрицательной функцией (рис. 4).

Рис. 4. Плотность распределения

непрерывной случайной величины.

Площадь, ограниченная осью х, прямыми х = х ₁ и х = х ₂ и кривой плотности распределения, равна вероятности того, что случайная величина примет значения из интервала х ₁ ¸ х ₂:

Р (х ₁ £ Х £ х ₂) = 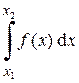= F (х ₂) - F (х ₁). (1.33)

Тогда

F (х) = Р (-¥ £ Х £ х)= 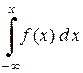. (1.34)

Поскольку попадание случайной величины в интервал -¥ < Х < +¥ есть достоверное событие, то

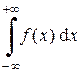= 1. (1.35)