 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Алгоритм. 1. Шаг 1. Задаются начальные границы отрезка и число итераций , рассчитывают начальные точки деления: и значения в них целевой функции: .
|
|
1. Шаг 1. Задаются начальные границы отрезка 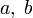 и число итераций
и число итераций 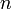 , рассчитывают начальные точки деления:
, рассчитывают начальные точки деления: 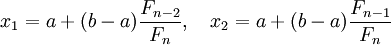 и значения в них целевой функции:
и значения в них целевой функции: 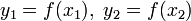 .
.
2. Шаг 2. 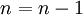 .
.
§ Если 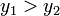 , то
, то 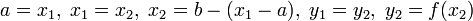 .
.
§ Иначе 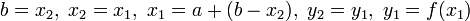 .
.
3. Шаг 3.
§ Если 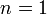 , то
, то 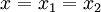 и останов.
и останов.
§ Иначе возврат к шагу 2.
11. Методы безусловной минимизации выпуклых функций многих переменных:
Метод покоординатного спуска (Метод Гаусса-Зейделя )
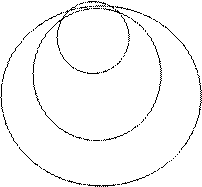
Данный метод легко проиллюстрировать геометрически для случая двух переменных. Рассмотрим функцию двух переменных 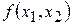
x2 
 |
Е

 x12
x12 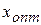
Д С


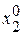

 А В
А В
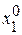
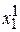 х1
х1
Предполагаем, что в 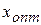 - функция имеет min. Выбираем начальную точку А (
- функция имеет min. Выбираем начальную точку А (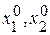 ). И вычисляем значение целевой функции в этой точке (
). И вычисляем значение целевой функции в этой точке (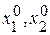 ). Затем фиксируем координату
). Затем фиксируем координату 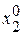 и изменяя первую переменную х1 двигаемся в направлении убывания функции f до тех пор, пока не дойдем до минимума, при
и изменяя первую переменную х1 двигаемся в направлении убывания функции f до тех пор, пока не дойдем до минимума, при 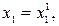 вычисляем в этой точке В значение целевой функции и сравниваем его с предыдущим значением целевой функции.
вычисляем в этой точке В значение целевой функции и сравниваем его с предыдущим значением целевой функции.
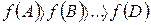
Фиксируем координату 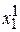 и начинаем изменять координату x2. Изменение координаты x2 будет происходить, пока целевая функция уменьшается. Затем снова фиксируем координату x12 и измеряем координату х1, таким образом мы должны прийти к оптимуму.
и начинаем изменять координату x2. Изменение координаты x2 будет происходить, пока целевая функция уменьшается. Затем снова фиксируем координату x12 и измеряем координату х1, таким образом мы должны прийти к оптимуму.
Окончания процесса оптимизации является следующее условие:
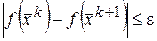
12. Методы безусловной минимизации выпуклых функций многих переменных:метод градиентного спуска
Выбираем начальную точку, вычисляем в ней градиент функции и делаем небольшой шаг в обратном антиградиентном направлении (ищем min).
В результате пришли в точку, в которой значение целевой функции больше первоначального.
В новой точке повторяем процедуру: вычисляем grad функции и делаем шаг в антиградиентном направлении. Таким образом, будет двигаться в сторону убывания функции формула, по которой осуществляется поиск вычисления экстремума функции:
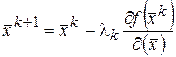 (1)
(1)
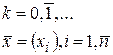
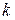 - число шагов (итераций)
- число шагов (итераций)
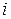 - число переменных (коэффициентов)
- число переменных (коэффициентов)
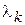 - шаг
- шаг
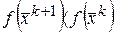 (2)
(2)
шаг 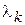 выбираем из условия убывания функции на каждом этапе вычисления. Наиболее простой способ выбора шага – это берут одно и то же значение шага:
выбираем из условия убывания функции на каждом этапе вычисления. Наиболее простой способ выбора шага – это берут одно и то же значение шага:
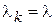
если при этом выполняется условие (2).
При нарушении условия (2) число 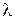 уменьшают, пока условие (2) не восстанавливается. Процесс заканчивается при достижении условия:
уменьшают, пока условие (2) не восстанавливается. Процесс заканчивается при достижении условия:
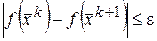
13. Методы безусловной минимизации выпуклых функций многих переменных:метод наискорейшего спуска
При применении метода градиентного спуска на каждом шаге нужно вычислять значения всех частных производных по всем переменным. Это замедляет вычислительный процесс. Так как вычисление градиента более сложная операция, чем вычисление самой функции, поэтому часто используют метод наискорейшего спуска.
Берем начальную точку 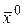 . вычисляем в ней значение grad и будем двигаться антиградиентным направлением до тех пор, пока это приводит к уменьшению целевой функции. То есть делаем не маленький шаг как в методе градиентного спуска.
. вычисляем в ней значение grad и будем двигаться антиградиентным направлением до тех пор, пока это приводит к уменьшению целевой функции. То есть делаем не маленький шаг как в методе градиентного спуска.
Точка 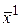 - в которой функция перестает уменьшаться является точкой ее min в направлении:
- в которой функция перестает уменьшаться является точкой ее min в направлении: 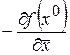
В точке 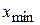 вычисляем снова grad и двигаемся в антиградиентном направлении до тех пор, пока целевая функция уменьшается и т.д.
вычисляем снова grad и двигаемся в антиградиентном направлении до тех пор, пока целевая функция уменьшается и т.д.
таким образом очередная точка 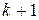 вычисляется по формуле:
вычисляется по формуле:
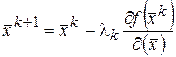
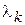 - шаг непостоянен. А мы его должны вычислить из условия минимума функции:
- шаг непостоянен. А мы его должны вычислить из условия минимума функции:
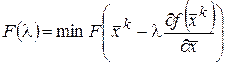
Эта функция одной переменной и для определения шага можно использовать методы одномерной оптимизации (метод простого перебора, метод золотого сечения, метод дихотомии).
14.Методы штрафных функций
Методы штрафных функций относятся к группе непрямых методов решения задач нелинейного програмирования:
Математическая модель задачи минимизации функции при наличии ограничений:

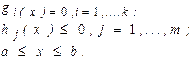
Они преобразуют задачу с ограничениями в последовательности задач безусловной оптимизации некоторых функций. Последние получаются путем модификации целевой функции с помощью функций-ограничений таким образом, чтобы ограничения в явном виде в задаче оптимизации не фигурировали. Это обеспeчивает возможность применения методов безусловной оптимизации. В общем случае вспомогательная функция имеет вид
F(x, а)= f(x) + Ф(x, a).
Здесь f(x) - целевая функция задачи оптимизации; Ф(х, a) - "штрафная" функция; параметр. Точку безусловного минимума функции будем обозначать через x(a).
В зависимости от вида различают методы внутренних штрафных, или барьерных, функций и методы внешных функций.
Методы внутренних штрафных функций.Эти методы применяются для решения задач нелинейного програмирования с ограничениями-неравенствами. В рассматриваемых методах функции Ф(x, a) подбирают такими, чтобы их значения неограниченно возрастали при приближение к границе допустимой области G.
Общий вид внутренней штрафной функции: Ф(x, a) = 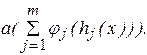
Методы внешних штрафных функций. Данные методы применяются для решения задачи оптимизации в общей постановке, т. е. при наличии как ограничений-неравенств, так и ограничений-равенств. В рассматриваемых методах функции Ф(x, a) выбирают такими, что из значения равны нулю внутри и на границе допустимой области G, а вне ее - положительны и возрастают тем больше, чем сильнее нарушаются ограничения. Таким образом, здесть "штрафуется" удаление от допустимой области G. Общий вид внешней штрафной функции:
Ф(x, a) = 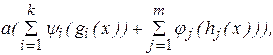
где 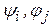 - функции, определяемые соответственно ограничениями-равенствами и неравенствами исходной задачи нелинейного программирования.
- функции, определяемые соответственно ограничениями-равенствами и неравенствами исходной задачи нелинейного программирования.
15.Постановка задачи линейного программирования (ЛП)Эквивалентные формы задач линейного программирования
Важный класс оптимизационных задач составляют линейные задачи, в которых целевая функция линейно зависит от управляющих параметров и систем уравнений или неравенств, условия ограничений также является линейной функцией.
К задачам линейного программирования сводятся задачи планирования производства, приготовления оптимальных смесей, раскроя материалов и т.д. Для определения оптимального решения используется симплекс-метод. Ниже рассматриваются примеры составления математического описания основных задач линейного программирования.
Эквивалентные формы линейного программирования
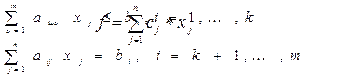 |
Общая задача линейного программирования. Она состоит в определении максимального (минимального) значения целевой функции:
при условиях
Условие неотрицательности: x j >= 0 (4) может быть наложено не на все переменные (j = 1,…, l; l ≤n).
Как известно, существуют три основные формы записи задачи линейного программирования. Эти формы запишем более подробно.
1. Общая задача имеет вид: 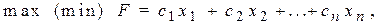
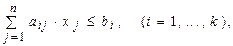
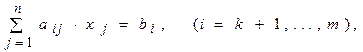
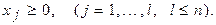
2. Стандартная (симметричная) задачаимеет вид: 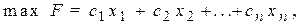
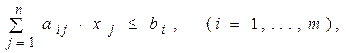
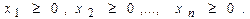 В стандартной задаче соотношение между числом неизвестных n и числом уравнений m может быть произвольным (
В стандартной задаче соотношение между числом неизвестных n и числом уравнений m может быть произвольным (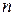 > m, n = m, n < m).
> m, n = m, n < m).
3. Каноническая задачаимеетвид: 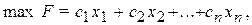
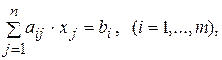
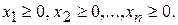
В канонической задаче число неизвестных всегда больше числа уравнений (n > m).
Частным случаем канонической задачи является задача в базисной форме, в которой все свободные члены в условиях ограничения неотрицательны (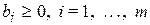 ), и каждая переменная
), и каждая переменная 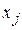 входит только в одно уравнение с коэффициентом 1. Такая переменная
входит только в одно уравнение с коэффициентом 1. Такая переменная 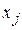 называетсябазисной.
называетсябазисной.
16. Графический метод
Графический метод решения задач ЛП основаны на геометрической интерпретации этих задач. Он применяется при решении задач двумерного пространства (целевая функция зависит от 2-х параметров 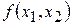 ). Задачу пространства размерности более 3-х изобразить на графике не возможно. В задачах ЛП всегда имеются ограничения задающие область допустимых решений.
). Задачу пространства размерности более 3-х изобразить на графике не возможно. В задачах ЛП всегда имеются ограничения задающие область допустимых решений.
Найти максимальное значение функции:
1) 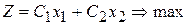
при условиях ограничения:
2) 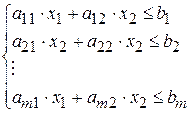
3) 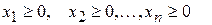
Система неравенств (2) при условии (3), если она имеет хотя бы одно решение, она называется совместной, в противном случае она несовместна.
Каждое неравенство системы (2) геометрически определяет полуплоскость граничной прямой:
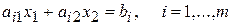
Условия неотрицательности (3) определяет полуплоскости граничными прямыми х1=0, х2=0.
Общая схема решения
1. Строят прямые, уравнения которых получаются в результате замены в ограничениях (2) и (3) знаков неравенств на знаки точных равенств.
2. Находят полуплоскости, определяемые каждым из ограничений задачи.
3. Находят многоугольник решений.
1. Строят вектор 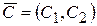
2. Строят прямую, 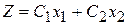 , проходящую через многоугольник решений.
, проходящую через многоугольник решений.
3. Передвигают эту прямую в направлении перпендикулярном вектор 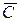 , в результате чего, либо находят точку в которой целевая функция принимает max значение, либо устанавливают неограниченность сверху функции.
, в результате чего, либо находят точку в которой целевая функция принимает max значение, либо устанавливают неограниченность сверху функции.
4. Определяют координаты точки максимальной функции и вычисляют значение целевой функции в этой точке.
17. Симплекс-метод решения задач ЛП. Алгоритм симплексного метода.
Для решения задачи линейного программирования в канонической форме разработан симплекс-метод. Симплекс-метод решения задачи линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план и каждый ее опорный план является невырожденным).
1. В последней строке симплекс-таблицы находят наименьший среди отрицательных приведенных коэффициентов 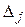 . Переменную для перевода в базисную выбирают из условия:
. Переменную для перевода в базисную выбирают из условия:
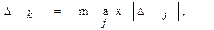 для
для 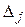 <0. (3.29)
<0. (3.29)
Свободная переменная 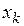 переводится в базисную. Столбец, соответствующий этому элементу, считается разрешающим (
переводится в базисную. Столбец, соответствующий этому элементу, считается разрешающим (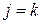 ).
).
2. Вычисляются отношение свободных членов к положительным элементам разрешающего столбца. Находят наименьшее из этих отношений, оно соответствует разрешающей строке (i = r):
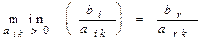 . (3.30)
. (3.30)
Элемент ark называется разрешающим. Базисная переменная 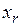 становится свободной переменной.
становится свободной переменной.
3. После нахождения разрешающего элемента и определения новой базисной переменной, переходят к следующей симплекс-таблице. Свободные члены 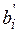 вычисляются по формулам:
вычисляются по формулам:
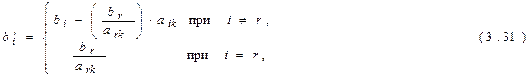
а коэффициенты при переменных 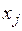 – по формулам:
– по формулам:
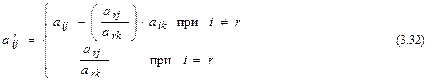
После вычисления 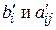 согласно формулам (3.31) и (3.32) их значения заносят в табл. 3.4. Элементы (m + 1)-й строки этой таблицы вычисляются либо по формулам:
согласно формулам (3.31) и (3.32) их значения заносят в табл. 3.4. Элементы (m + 1)-й строки этой таблицы вычисляются либо по формулам:
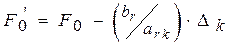 , (3.33)
, (3.33)
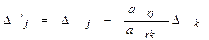 , (3.34)
, (3.34)
либо на основании их определения (3.28) - (3.29).4. Как только получится симплекс-таблица, в которой в последней строке все приведенные коэффициенты положительные, то оптимальный план получен и максимум целевой функции определен.
Дата публикования: 2015-07-22; Прочитано: 429 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
