Определение оптимального сечения балки при изгибе

Заданы размер l, нормативные нагрузки F_н, M_н, q_н, предел текучести материала s_т и коэффициенты надёжности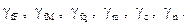

Требуется:

1. Построить эпюры поперечной силы Q и изгибающего момента М.

2. Из расчёта по предельным состояниям подобрать прокатный двутавр, размеры поперечного сечения в виде круга и прямоугольника с заданным соотношением сторон h/b.

3. По максимальному значению поперечной силы определить касательные напряжения на нейтральной оси и проверить прочность.

4. Сравнить варианты балки по расходу материала и выбрать наиболее оптимальное сечение.

Исходные данные

Шифр	l м	h/b	Fн кН	Mн кНм	qн кН/м	sт МПа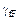
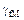
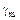
31–5	2,6	1,7					1,15	1,10	1,35	1,15	0,9	1,0

Расчётная схема и эпюры

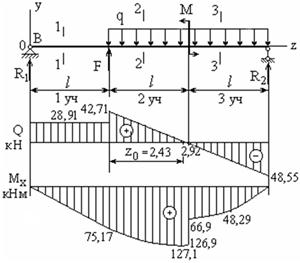
Рис. 1

Решение

Заданы нормативные значения сопротивления материала и нагрузок. Расчётные значения нагрузок получим, умножая нормативные величины на коэффициент надёжности по нагрузке:

F = F_н 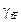= 12 · 1,15 = 13,8 кН,

M = M_н 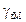= 50 · 1,2 = 60 кНм,

q = q_н 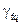= 13 · 1,35 = 17,55 кН/м.

Нормативное сопротивление равно пределу текучести, т.е. R_н = s_T = 360 МПа. Расчётное сопротивление материала будет

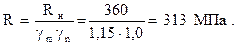
Проведём координатные оси y и z, как отмечено на расчётной схеме. Покажем опорные реакции R₁ и R₂. При определении внутренних сил понадобятся опорные реакции, потому определим их с помощью уравнений равновесия. Целесообразно сначала составить такое уравнение равновесия, которое будет содержать только одно из неизвестных. Наметим точку В и составим уравнение

,

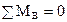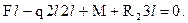
Разделим все слагаемые на l и найдём R₂

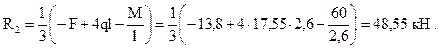
Составим второе уравнение равновесия

,

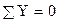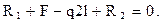
Отсюда

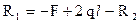= –13,8 + 2·17,55·2,6 – 48,55 = 28,91 кН.

Далее приступаем к определению внутренних сил Q и М_х в сечениях балки с помощью метода сечений. Разобьём балку по длине на 3 участка и обозначим их. Рассмотрим каждый участок отдельно. Проведём внутри них произвольные сечения 1–1, 2–2, 3–3.

1 участок z 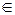[0; ]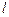

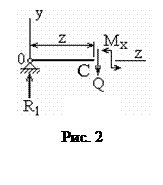Целесообразно рассмотреть левую отсечённую часть балки (рис. 2), так как к ней приложено меньше нагрузок, и это повлечёт меньший объём вычислений. Покажем оси y, z, переменное расстояние z, точку С, поперечную силу Q, изгибающий момент М_х. Для внутренних сил здесь и далее избираются положительные направления, что позволяет получить ответы, учитывающие установленные правила знаков. Они заключаются в том, что положительные поперечные силы создают момент по часовой стрелке относительно отсечённой части, положительные изгибающие моменты растягивают нижние волокна. Получим их из уравнений равновесия. Первое из них даёт поперечную силу

,

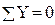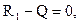
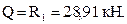
Эта величина постоянная, т.е. не зависит от z, поэтому на первом участке эпюра Q является горизонтальной прямой линией.

Cоставим второе уравнение равновесия и найдём изгибающий момент

, ,

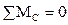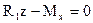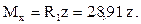
При составлении этого уравнения момент силы относительно точки С, направленный по часовой стрелке принят со знаком плюс. Изгибающий момент в сечениях является линейной функцией z. Поэтому найдём значения только на концах участка

,

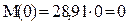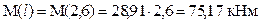
По этим результатам строим эпюру изгибающих моментов первого участка в виде прямой линии.

2 участок z 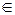[0; l ]

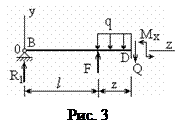
Рассмотрим левую отсечённую часть балки (рис. 3). Укажем на схеме оси y, z, точку D, поперечную силу Q, изгибающий момент М_х.

Поперечную силу находим из уравнения равновесия

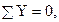
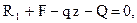
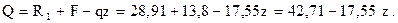
Поперечная сила является линейной функцией координаты сечения. Необходимо находить значения в двух точках

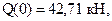
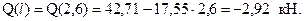
Строим эпюру для этого участка.

Воспользуемся уравнением равновесия для определения изгибающего момента

,

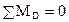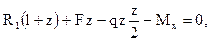
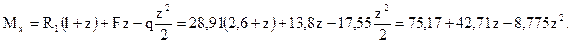
Полученный результат свидетельствует, что эпюра изгибающих моментов на этом участке является криволинейной, поэтому необходимо иметь три её точки. Очевидно, что две точки целесообразно иметь на концах участка. Положение же третьей точки не совпадает с серединой участка и должно быть установлено специально. Дело в том, что поперечная сила в некотором сечении этого участка обращается в нуль, и из этого следует, что изгибающий момент в нём является экстремумом функции изгибающего момента. В этом месте поперечная сила меняет знак с плюса на минус, поэтому экстремум является конкретно максимумом. Чтобы установить положение этого сечения, приравняем поперечную силу к нулю

.

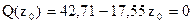Отсюда имеем

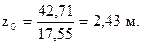
Подставим это значение в (2) и найдём максимум функции изгибающего момента на этом участке

кНм.

Для построения эпюры находим ещё изгибающие моменты в концевых сечениях

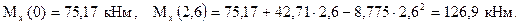
Строим соответствующую эпюру по трём значениям в виде кривой линии.

3 участок z 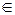[0; l ]

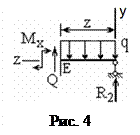Для этого участка целесообразнее использовать правую отсечённую часть (рис. 4). Указываем на схеме оси y, z, точку Е, поперечную силу Q, изгибающий момент М_х.

Составим уравнение равновесия и определим из него поперечную силу.

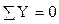, Q – qz + R₂ = 0,

(1)

Получена линейная функция, поэтому находим два значения поперечной силы

Q(0) = –48,55 кН,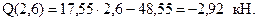

Второе значение совпадает с результатом для данного сечения, полученным во втором участке.

Теперь найдём изгибающие моменты.

, ,

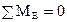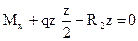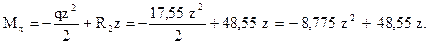(2)

В трёх точках участка

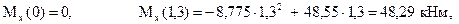
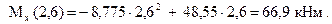
По результатам счёта построены эпюры M и Q, показанные на рис. 1.

Теперь перейдём к подбору сечений. Опасным является сечение с максимальным изгибающим моментом М_max = 127,1 кНм. Требующиеся размеры поперечных сечений и номер двутавра найдутся из условия прочности, которое имеет вид

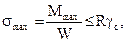(1)

где W – искомый осевой момент сопротивления поперечного сечения. Определим его из (1)

.

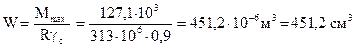Определим сечения, соответствующие такому значению момента сопротивления.

Двутавр

По таблице сортамента наиболее подходящим является двутавр № 30 с осевым моментом сопротивления W = 472 см³, осевым моментом инерции J = 7080 см⁴, площадью сечения А_д = 46,5 см², статическим моментом полусечения S = 268 см³, с толщиной стенки d = 0,65 см.

Проверим прочность по касательным напряжениям. В сечении с наибольшей поперечной силой должно выполняться условие

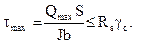(2)

Здесь R_s – расчётное сопротивление материала балки при сдвиге, b – ширина сечения на уровне нейтрального слоя, т.е. b = d = 0,65 см. Для стали в данной балке

R_s= 0,6R = 0,6·313 = 187,8 МПа.

Подставляя численные значения в (2), получим

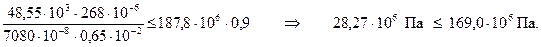
Очевидно, что условие прочности выполняется.

Прямоугольник

Осевой момент сопротивления прямоугольника вычисляется по формуле

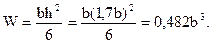
Приравнивая его к найденному выше значению, находим

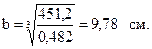
Высота сечения и его площадь составляют

h = 1,7 · 9,78 = 16,6 см, A_п = 9,78 · 16,6 = 162,6 см².

Условие прочности по касательным напряжениям имеет вид

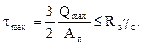(3)

Численные подстановки в (3) дают

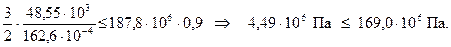
Условие прочности выполняется.

Круг

Аналогично находим диаметр и площадь сечения.

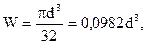
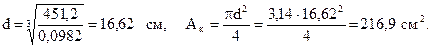
Проверим условие прочности по касательным напряжениям

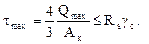(4)

Подставляя числа, имеем

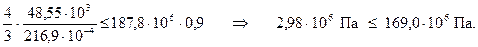
Условие прочности (4) выполняется.

Соотношения между найденными площадями имеют вид

А_д:А_п: А_к = 1: 3,5: 4,66.

Поскольку расход материала прямо зависит от площади поперечного сечения балки, отсюда следует, что балка из двутавра является наиболее оптимальной. Её площадь сечения многократно меньше, чем в остальных случаях.

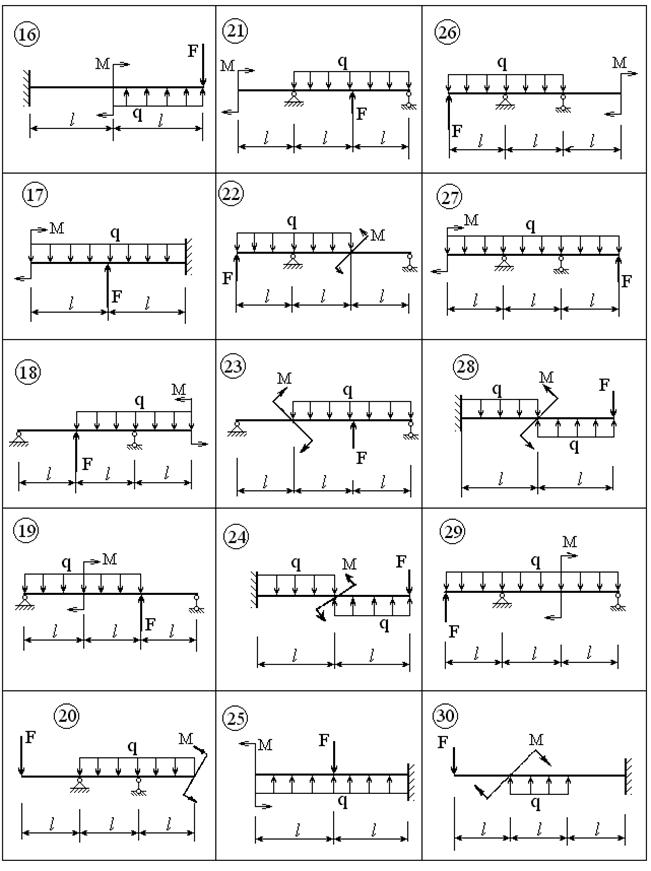
ВАРИАНТЫ ЗАДАНИЙ

Второе число шифра	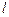м	h/b	Fн кН	Mн кНм	qн кН/м	sт МПа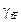
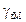
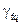
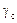
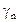
	2,5	1,9					1,10	1,15	1,35	1,05	0,80	0,85
	2,4	1,5					1,05	1,10	1,30	1,15	0,90	1,10
	2,2	2,0					1,15	1,20	1,25	1,10	0,85	1,15
	2,3	1,8					1,20	1,25	1,40	1,05	0,95	1,00
	2,1	1,6					1,11	1,18	1,38	1,12	0,88	1,13