Типовые примеры. Пример 5.1.Известна информация об интенсивности страховых случаев (отношение страховых выплат к страховым поступлениям) 140 страховых компаний (табл

Пример 5.1. Известна информация об интенсивности страховых случаев (отношение страховых выплат к страховым поступлениям) 140 страховых компаний (табл. 5.1).

Таблица 5.1

Интенсивность страховых случаев 140 страховых компаний для примера 5.1

Интенсивность страховых случаев	Количество страховых компаний
0,01—0,12
0,12—0,23
0,23—0,34
0,34—0,45
0,45—0,56
0,56—0,67
0,67—0,78
0,78—0,89

Осуществите расчет основных характеристик вариационного ряда, выравнивание по кривой нормального распределения, проверку по основным критериям согласия.

Решение

Имеющаяся информация об интенсивности страховых случаев (отношение страховых выплат к страховым поступлениям) 140 страховых компаний представляет собой интервальный вариационный ряд распределения (табл. 5.2), где интенсивность страховых случаев — изучаемый признак в виде интервала, а количество страховых компаний — частота (вес) признака. Осуществим расчет накопленных частот в графе 2 табл. 5.2.

Таблица 5.2

Вариационный ряд распределения

Интервал	Частота	Накопленная частота
А
0,01—0,12
0,12—0,23
0,23—0,34
0,34—0,45
0,45—0,56
0,56—0,67
0,67—0,78
0,78—0,89

Далее рассчитаем характеристики вариационного ряда. Осуществим расчет вспомогательных значений для определения среднего значения интенсивности страховых случаев в графах 2, 3 табл. 5.3.

Таблица 5.3

Расчет среднего значения ряда распределения

Интервал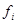
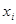
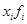
А
0,01—0,12		0,065	0,78
0,12—0,23		0,175	2,80
0,23—0,34		0,285	5,70
0,34—0,45		0,395	11,46
0,45—0,56		0,505	12,12
0,56—0,67		0,615	9,23
0,67—0,78		0,725	10,15
0,78—0,89		0,835	8,35
Итого		—	60,58

Среднее значение интервального ряда распределения определяется по формуле средней арифметической взвешенной:

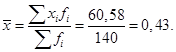
Средняя интенсивность страховых случаев в одной компании по договорам страхования за изучаемый период составляет 0,43.

Определим модальный интервал: так как наибольшая частота в графе 1 табл. 5.2 составляет 29 страховых фирм, то модальный интервал будет от 0,34 до 0,45. Мода составит

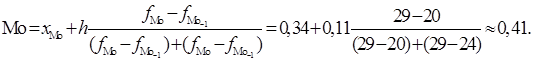
Наиболее часто встречающееся значение интенсивности страховых случаев — 0,41.

Определим медианный интервал (интервал, в котором сумма накопленных частот превысит половину общего числа наблюдений): половина изучаемой совокупности представляет собой 70 страховых фирм, последняя из которых находится в интервале от 0,34 до 0,45, являющимся медианным интервалом (графа 2 табл. 5.2). Медиана составит

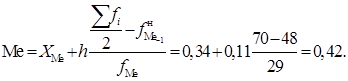
В одной половине исследуемых страховых компаний интенсивность страховых случаев находится ниже 0,42 в другой половине — выше 0,42.

По соотношению можно сделать предварительный вывод, что изучаемое распределение близко к нормальному закону распределения.

Первая квартиль:

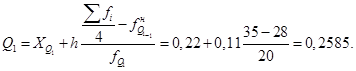
В четверти всех страховых компаний интенсивность страховых случаев колеблется от 0,01 до 0,2585.

Третья квартиль:

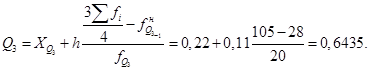
В 75% всех страховых компаний интенсивность страховых случаев колеблется от 0,01 до 0,6435.

Необходимые для определения основных характеристик вариационного ряда величины приведены в табл. 5.4.

Таблица 5.4

Расчет вспомогательных величин для характеристики вариационного ряда

Интервал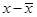
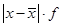
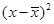
А
0,01—0,12	–0,367714286	4,412571429	0,135213796	1,622565551
0,12—0,23	–0,257714286	4,123428571	0,066416653	1,062666449
0,23—0,34	–0,147714286	2,954285714	0,02181951	0,436390204
0,34—0,45	–0,037714286	1,093714286	0,001422367	0,041248653
0,45—0,56	0,072285714	1,734857143	0,005225224	0,125405388
0,56—0,67	0,182285714	2,734285714	0,033228082	0,498421224
0,67—0,78	0,292285714	4,092	0,085430939	1,196033143
0,78—0,89	0,402285714	4,022857143	0,161833796	1,618337959
Итого	-	25,25	—	6,6

Продолжение таблицы 5.4

Интервал
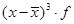
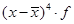
А
0,01—0,12	–0,049720044	–0,596640533	0,0183	0,2194
0,12—0,23	–0,01711652	–0,273864325	0,0044	0,0706
0,23—0,34	–0,003223053	–0,064461067	0,0005	0,0095
0,34—0,45	–5,36436E-05	–0,001555663	0,0000	0,0001
0,45—0,56	0,000377709	0,009065018	0,0000	0,0007
0,56—0,67	0,006057005	0,090855069	0,0011	0,0166
0,67—0,78	0,024970243	0,349583401	0,0073	0,1022
0,78—0,89	0,065103424	0,651034242	0,0262	0,2619
Итого	—	0,16	—	0,6808

Размах вариации:

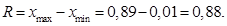
Среднее линейное отклонение (взвешенное):

Амплитуда колебаний интенсивности страховых случаев составляет 0,88.

Среднее квадратичное отклонение (взвешенное):

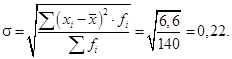
В среднем варианты интенсивности страховых случаев отклоняются от среднего значения на 0,22.

Дисперсия (взвешенная):

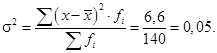
Средний квадрат отклонений интенсивности страховых случаев от их средней величины составляет 0,05.

Коэффициент осцилляции:

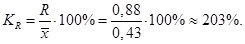
Относительная колеблемость крайних значений интенсивности страховых случаев вокруг средней велика, следовательно, высока вариация признака.

Линейный коэффициент вариации:

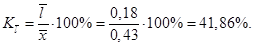
Доля усредненного значения абсолютных отклонений интенсивности страховых случаев от средней величины составляет 41,86%.

Коэффициент вариации:

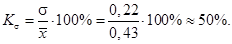
Так как 50% > 33%, совокупность неоднородная, коэффициент вариации высокий.

Коэффициент асимметрии:

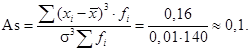
Аs > 0, значит, асимметрия правосторонняя.

Эксцесс распределения:

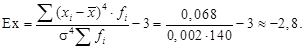
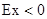, следовательно, эксцесс распределения — низковершинный.

Эмпирическое распределение изобразим графически с помощью гистограммы распределения на рис. 5.5.

Рис. 5.5. Гистограмма распределения интенсивности распределения страховых случаев 140 страховых компаний

Осуществим выравнивание по теоретической кривой нормального распределения.

Теоретические частоты для распределения определим в графе 3 табл. 5.5 по формуле

.

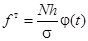Таблица 5.5

Расчет теоретических частот вариационного ряда

Интервал	t	j(t)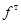
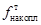
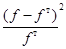
А
0,01—0,12	–1,69	0,0957			3,5714
0,12—0,23	–1,18	0,1989			0,2857
0,23—0,34	–0,68	0,3166			0,1818
0,34—0,45	–0,17	0,3932			0,0357
0,45—0,56	0,33	0,3778			0,3333
0,56—0,67	0,84	0,2803			1,2500
0,67—0,78	1,35	0,1604			0,8181
0,78—0,89	1,85	0,0721			5,0000

Критерий согласия Пирсона:

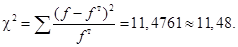
Определим табличное значение критерия Пирсона:

k = 8 – 3 = 5, α = 99%, n = 0,01, c² = 11,48.

Расхождение между фактическим и теоретическим распределением случайно, а распределение хорошо согласуется с законом нормального распределения.

Критерий согласия Романовского:

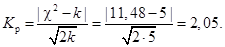
Имеем 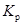< 3, значит, расхождение между фактическим и теоретическим распределением случайно.

Критерий согласия Колмогорова:

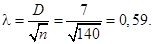
Имеем 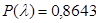. Следовательно, с вероятностью 86,43% можно утверждать, что гипотеза о нормальном распределении не отвергается, а расхождения эмпирического и теоретического распределений носят случайный характер.

Построим эмпирическое и теоретическое распределения графически (рис. 5.6).

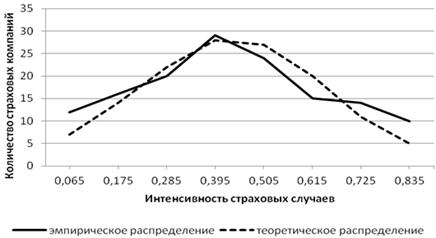
Рис. 5.6. Эмпирическое и теоретическое распределения интенсивности распределения страховых случаев 140 страховых компаний

Пример 5.2. Известна следующая информация о распределении клиентов туристической фирмы (табл. 5.6).

Таблица 5.6

Распределение клиентов по числу посещений туристической фирмы для примера 5.2

Количество посещений	Частота (количество чел.)	Накопленная частота
Итого		—

Осуществите построение кумуляты для дискретного ряда.

Решение

Построение кумуляты для дискретного ряда осуществим на основе ряда накопленных частот: по оси абсцисс откладываем значения признака — количества посещений, по оси ординат — накопленные частоты (рис. 5.7).

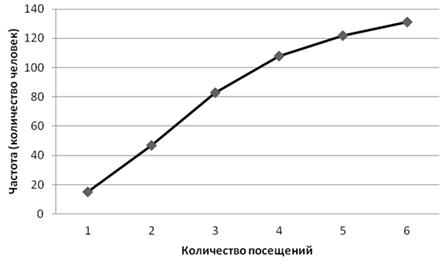
Рис. 5.7. Кумулята распределения клиентов по числу посещений туристической фирмы

Пример 5.3. Известна информация о распределении путевок в туристической фирме в зависимости от затрат времени на поездку (табл. 5.7).

Таблица 5.7

Распределение путевок в зависимости от затрат времени на поездку

Затраты времени в пути до турбазы, мин	Количество путевок
А
20—25
25—30
30—40
40—60
60—90
Всего

Осуществите расчет частостей, абсолютной и относительной плотностей, накопленной частоты и постройте кумуляту для интервального ряда.

Решение

Расчет частостей, абсолютной и относительной плотностей, накопленной частоты осуществим в табл. 5.8 соответственно в графах 2, 4, 5 и 6. Построение кумуляты для интервального ряда осуществим на основе ряда накопленных частот: по оси абсцисс откладываем значения признака — затраты времени в пути до турбазы, по оси ординат — накопленные частоты (рис. 5.8).

Таблица 5.8

Расчет параметров

Затраты времени в пути до турбазы, мин	Количество путевок	Частость (доля)	Длина интервала	Абсолютная плотность	Относительная плотность	Накопленная частота
А
20—25		0,3		6,00	0,0600
25—30		0,2		4,00	0,0400
30—40		0,2		2,00	0,0200
40—60		0,15		0,75	0,0075
60—90		0,15		0,50	0,0050
Всего		1,0	—	—	—	—

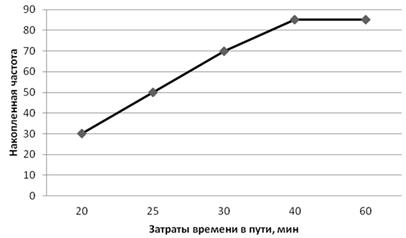
Рис. 5.8. Кумулята распределения путевок в зависимости от затрат времени на поездку

Пример 5.4. Выполним выравнивание эмпирических частот, приведенных в табл. 5.9, по нормальному закону.

Таблица 5.9

Эмпирических частоты для примера 5.4

Эмпирические данные, х	Эмпирическая частота, m
А
Всего

Решение

Для вычисления 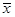используется формула взвешенной средней арифметической 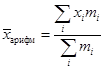; получаем 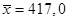. Для расчета s используется формула 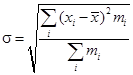; получаем s = 13, 60. Имеем N = 100; h_k = 10.

Расчет теоретических частот осуществим в табл. 5.10.

Таблица 5.10

Выравнивание эмпирических частот по нормальному закону

Эмпирические данные, х	Эмпирическая частота, m		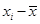t	Ф(t)	Теоретические частоты
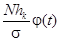
	m ¢
А
			2,43	0,021	1,5
			1,69	0,096	7,1
			0,96	0,252	18,5
			0,22	0,389	28,6
		–7	0,51	0,350	25,7
		–17	1,25	0,183	13,5
		–27	1,99	0,055	4,0
		–37	2,72	0,010	0,7
Всего		—	—	—	99,6

Эмпирические и теоретические частоты распределения изобразим графически на рис. 5.9.

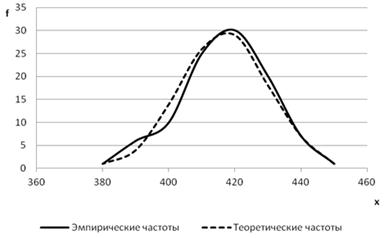
Рис. 5.9. Выравнивание эмпирических частот по закону нормального распределения

Пример 5.5. Проведем выравнивание эмпирических частот, приведенных в табл. 5.11, по закону Вейбулла.

Таблица 5.11

Эмпирические частоты для примера 5.5

Эмпирические данные, х	Эмпирическая частота, m
Всего

Решение

Имеем N = 48; h_k = 436; 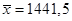; s = 754,6; V = 0,52 (для расчета используется формула ). При V = 0,52 находим в[xxvii] = 2 и K _в= 0,886.

Определим значение параметра распределения[xxviii]:

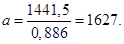
Необходимые для расчета величины приведем в табл. 5.12.

Таблица 5.12

Выравнивание эмпирических частот по закону Вейбулла

Эмпирические данные, х	Эмпирическая частота, m	x / а	аf (x / а)	Теоретические частоты
	m ¢
		1,98	0,0792	0,98
		1,71	0,1842	2,27
		1,44	0,3631	4,48
		1,17	0,5948	7,33
		0,90	0,8007	9,87
		0,64	0,8454	10,42
		0,37	0,6417	7,91
Всего		–	–	43,25

Эмпирические и теоретические частоты распределения Вейбулла изобразим графически на рис.5.10.

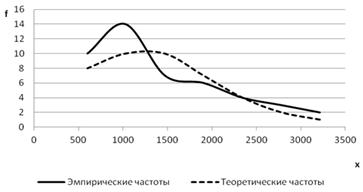
Рис. 5.10. Выравнивание эмпирических частот по закону Вейбулла

Пример 5.6. Проведем выравнивание эмпирического распределения (табл. 5.13) по экспоненциальному закону.

Таблица 5.13

Эмпирические частоты для примера 5.6

Эмпирические данные, х	Эмпирическая частота, m
Всего

Решение

Имеем N = 77; h_k = 36; .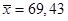

Рассчитанные величины приведем в табл. 5.14.

Таблица 5.14

Выравнивание эмпирических частот по экспоненциальному закону

Эмпирические данные, х	Эмпирическая частота, m		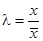e –l	Теоретические частоты
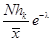
	m ¢
		3,37	0,0344	1,373
		2,85	0,0578	2,307
		2,33	0,0973	3,885
		1,81	0,1637	6,535
		1,30	0,2725	10,880
		0,78	0,4584	18,301
		0,26	0,7710	30,786
Всего		—	—	74,015

Эмпирические и теоретические частоты экспоненциального распределения изобразим графически на рис.5.11.

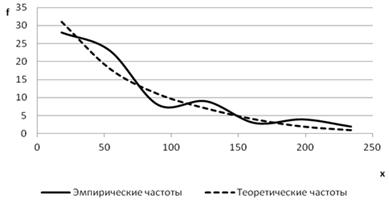
Рис. 5.11. Выравнивание эмпирических частот по экспоненциальному закону

Пример 5.7. Выполним выравнивание статистического ряда (табл. 5.15) по закону Пуассона с параметрами 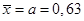(следовательно, 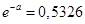); N = 400.

Таблица 5.15

Эмпирические частоты для примера 5.7

Эмпирические данные, х	Эмпирическая частота, m
Всего

Решение

Рассчитанные величины приведем в табл. 5.16

Таблица 5.16

Выравнивание эмпирических частот по закону Пуассона

Эмпирические данные, х	Эмпирическая частота, m	ax	x!	Теоретические частоты
	m ¢
				213,04
		0,64		136,35
		0,41		43,63
		0,26		9,316
		0,17		1,49
		0,11		0,19
Всего		—	—	404,01

Эмпирические и теоретические частоты распределения Пуассона изобразим графически на рис.5.12.

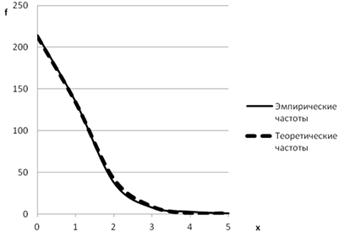
Рис. 5.12. Выравнивание эмпирических частот по распределению Пуассона

Пример 5.8. Применим критерий согласия Ястремского для проверки гипотезы о нормальном законе распределения для данных, приведенных в табл. 5.17.

Таблица 5.17

Эмпирические частоты для примера 5.8

Эмпирические данные, х	Эмпирическая частота, m
Всего

Решение

Поскольку в формуле расчета критерия согласия Ястремского применяется критерий согласия Пирсона, осуществим его расчет в табл.5.18.

Таблица 5.18

Расчет величин для определения критериев согласия Пирсона и Ястремского

Эмпирические данные, х	Эмпирическая частота, m	Теоретические частоты m ¢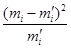
			0,222
			0,034
			0,038
			1,143
			1,000
Всего			2,438

.

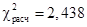Критерий согласия Ястремского:

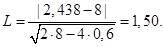
Эта величина меньше 3, следовательно, расхождения между эмпирическими и теоретическими частотами случайны.

Пример 5.9. Применим критерий согласия Колмогорова для проверки гипотезы о законе распределения Вейбулла для данных, приведенных в табл. 5.19.

Таблица 5.19

Эмпирические частоты для примера 5.9

Эмпирические данные х	Эмпирическая частота m
Всего

Решение

Рассчитанные величины приведем а табл. 5.20.

Таблица 5.20

Расчет критерия согласия Колмогорова

Эмпирические данные х	Эмпирическая частота m	Теоретические частоты m ¢	Накопленные эмпирические частоты F	Накопленные теоретические частоты F ¢	| F – F ¢|
Всего					–

При D = 4 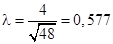. Согласно таблице данное значение λ находится между вероятностями 0,8643 и 0,9228, следовательно, при вероятности от 0,8643 до 0,9228 расхождения между эмпирическими и теоретическими частотами несущественны.