 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
ВВЕДЕНИЕ 7 страница. Для заданного положения механизма (рис. 97) определить скорость ползуна , угловую скорость звена
|
|
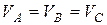 ,
,  .
.
Пример №13.
Для заданного положения механизма (рис. 97) определить скорость ползуна 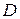 , угловую скорость звена
, угловую скорость звена 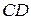 , если кривошип
, если кривошип  размером
размером 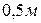 вращается с угловой скоростью
вращается с угловой скоростью 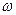 =1с-1,
=1с-1,  , длина звена
, длина звена 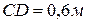 ,
, 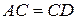 .
.
Решение.
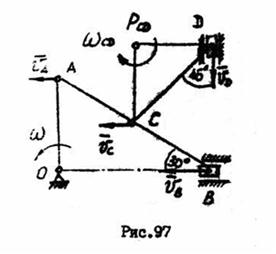
1. Определяем скорость точки  , принадлежащей кривошипу
, принадлежащей кривошипу  :
: 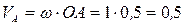 м/с. Вектор
м/с. Вектор 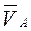 скорости точки
скорости точки  направлен перпендикулярно звену
направлен перпендикулярно звену  . Ползун
. Ползун  движется в горизонтальных направляющих. Векторы
движется в горизонтальных направляющих. Векторы 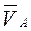 и
и 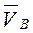 скоростей точек
скоростей точек  и
и  параллельны между собой. Мгновенный центр скоростей звена
параллельны между собой. Мгновенный центр скоростей звена  находится в бесконечности, что следует из соотношения:
находится в бесконечности, что следует из соотношения:
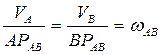 ,
,
где 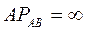 ,
, 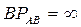 ,
, 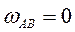 .
.
2.Следовательно, звено  совершает мгновенное поступательное движение. Все точки звена
совершает мгновенное поступательное движение. Все точки звена  движутся с одинаковыми по модулю и направлению скоростями, т.е.
движутся с одинаковыми по модулю и направлению скоростями, т.е.
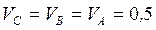 м/с.
м/с.
3. Ползун 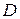 движется в вертикальных направляющих. Мгновенный центр скоростей звена
движется в вертикальных направляющих. Мгновенный центр скоростей звена 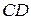 лежит в точке
лежит в точке 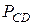 . Для звена
. Для звена 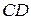 соблюдаются следующие соотношения:
соблюдаются следующие соотношения:
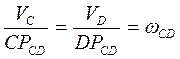 .
.
Так как 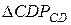 - равнобедренный,
- равнобедренный, 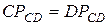 , скорости точек
, скорости точек 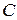 и
и 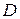 равны между собой:
равны между собой:
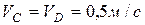 ;
;
угловая скорость звена 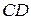 :
:  .
.
4. Если скорости точек  и
и  тела параллельны между собой и при этом линия
тела параллельны между собой и при этом линия  перпендикулярна вектору
перпендикулярна вектору 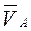 , то МЦС звена определяется геометрическим построением (рис. 98,а, б).
, то МЦС звена определяется геометрическим построением (рис. 98,а, б).
Численные значения скоростей точек  и
и  должны быть известны. Положение МЦС определяются из соотношения:
должны быть известны. Положение МЦС определяются из соотношения:
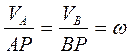
Пример №14.
Дифференциальный ворот состоит из двух валов  и
и  с радиусами
с радиусами  и
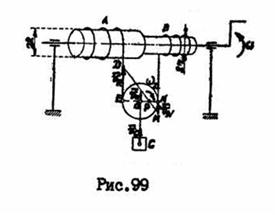
и 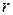 , где
, где  .
.
 На оба вала намотана одна нить, на которой находится подвижный блок радиуса
На оба вала намотана одна нить, на которой находится подвижный блок радиуса 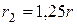 с подвешенным к нему грузом
с подвешенным к нему грузом 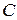 (рис. 99). Определить скорость груза, угловую скорость подвижного блока, если валам рукоятки сообщена угловая скорость
(рис. 99). Определить скорость груза, угловую скорость подвижного блока, если валам рукоятки сообщена угловая скорость 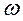 .
.
Решение:
1. Принимая, что нить наматывается без проскальзывания, выразим скорости точек 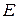 и
и 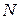 через угловую скорость барабана и его размеры:
через угловую скорость барабана и его размеры:
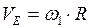 ;
; 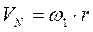 .
.
Подвижный блок совершает плоскопараллельное движение. Скорости двух точек блока 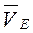 и
и 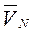 параллельны и направлены в противоположные стороны. Мгновенный центр скоростей блока – точку
параллельны и направлены в противоположные стороны. Мгновенный центр скоростей блока – точку  , найдем построением. Положение точки
, найдем построением. Положение точки  определим из соотношения:
определим из соотношения:
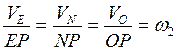 .
.
Из свойства пропорции получим:
 ;
;
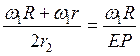 , откуда
, откуда
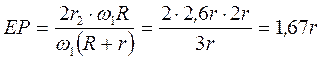 .
.
Угловая скорость подвижного блока:
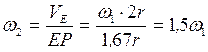 .
.
Скорость груза равна скорости центра блока, которая пропорциональна расстоянию точки 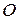 до мгновенного центра скоростей блока:
до мгновенного центра скоростей блока:
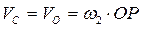 ;
;
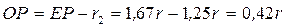 .
.
 .
.
Пример №15.
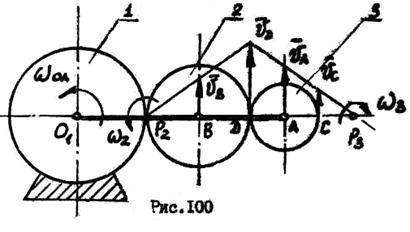
Для заданного положения механизма (рис. 100) определить скорости точек  ,
,  ,
, 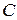 , угловые скорости всех его звеньев, если
, угловые скорости всех его звеньев, если 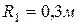 ,
, 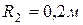 ,
, 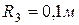 ,
, 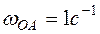 .
.
Решение:
Зная угловую скорость кривошипа  , найдем скорость точки
, найдем скорость точки  :
: 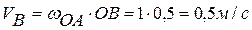
Для колеса  мгновенный центр скоростей находится в точке
мгновенный центр скоростей находится в точке 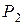 касания с неподвижным колесом 1. Угловая скорость колеса
касания с неподвижным колесом 1. Угловая скорость колеса  :
:
 .
.
Скорость точки 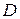 , принадлежащей колесу
, принадлежащей колесу  , пропорциональна расстоянию
, пропорциональна расстоянию  :
:
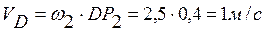
Найдем скорость точки  , принадлежащей кривошипу
, принадлежащей кривошипу  :
: 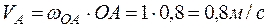
Скорости точек 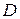 и
и  колеса 3 известны по модулю и направлению. Мгновенный центр скоростей колеса 3 находится в точке Р3. Положение точки Р3 найдем из соотношений
колеса 3 известны по модулю и направлению. Мгновенный центр скоростей колеса 3 находится в точке Р3. Положение точки Р3 найдем из соотношений
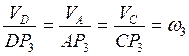 ;
;
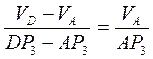 ;
;
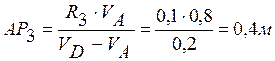 ;
;
 ;
;
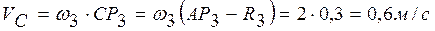 .
.
Пример №16.
Кривошип  (рис. 101) вращается с угловой скоростью
(рис. 101) вращается с угловой скоростью  . Колесо
. Колесо  , соединенное с кривошипом в точке
, соединенное с кривошипом в точке  , обкатывается по колесу
, обкатывается по колесу 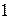 , вращающемуся с угловой скоростью
, вращающемуся с угловой скоростью 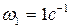 . Определить угловую скорость колеса
. Определить угловую скорость колеса  и скорость точки
и скорость точки 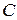 , если
, если 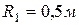 ,
, 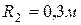 .
.
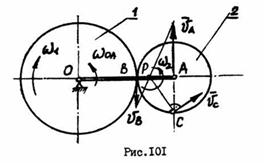 Решение:
Решение:
1. Найдем скорость точки  , принадлежащей кривошипу
, принадлежащей кривошипу  :
:  .
.
2. Определим скорость точки  , принадлежащей колесу 1, вращающемуся с угловой скоростью
, принадлежащей колесу 1, вращающемуся с угловой скоростью 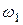 :
: 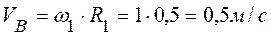 .
.
3. Для колеса  , совершающего плоское движение, известны скорости точек
, совершающего плоское движение, известны скорости точек  и
и  . Мгновенный центр скоростей колеса
. Мгновенный центр скоростей колеса  -точку
-точку 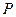 найдем построением. Угловую скорость колеса
найдем построением. Угловую скорость колеса  определим из соотношения:
определим из соотношения:
 .
.
Для определения положения мгновенного центра скоростей используем свойство пропорции:
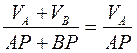 ;
;
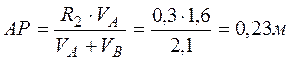
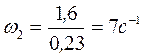 .
.
Скорость точки 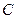 пропорциональна расстоянию
пропорциональна расстоянию 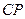 до МЦС:
до МЦС: 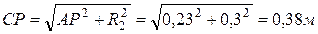 ;
;
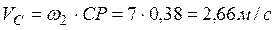 .
.
Вектор 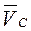 скорости точки
скорости точки 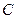 направлен перпендикулярно отрезку
направлен перпендикулярно отрезку 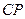 в сторону угловой скорости
в сторону угловой скорости 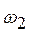 .
.
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ ТОЧЕК ТЕЛА ПРИ ПЛОСКОМ ДВИЖЕНИИ.
Ускорение любой точки  тела при плоском движении равно геометрической сумме ускорения точки, принятой за полюс, и ускорение точки в ее вращении вместе с телом вокруг оси, проходящей через полюс (рис. 102),
тела при плоском движении равно геометрической сумме ускорения точки, принятой за полюс, и ускорение точки в ее вращении вместе с телом вокруг оси, проходящей через полюс (рис. 102),
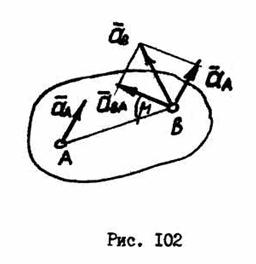
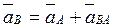 . (2.36)
. (2.36)
Вектор  направлен под углом
направлен под углом 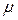 к отрезку АВ, где
к отрезку АВ, где
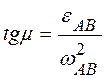 . (2.37)
. (2.37)
Так как значение угла 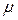 неизвестно, предварительно вектор
неизвестно, предварительно вектор  раскладывают на нормальную и касательную составляющие:
раскладывают на нормальную и касательную составляющие:
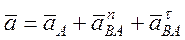 , (2.38)
, (2.38)
где 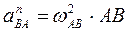 ,
, 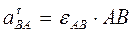 . (2.39)
. (2.39)
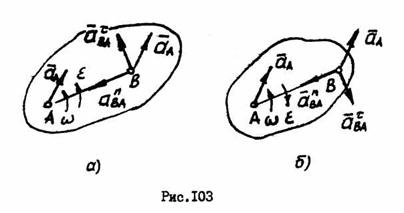
Вектор 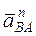 направлен всегда вдоль прямой
направлен всегда вдоль прямой 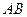 к полюсу
к полюсу 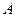 , вектор
, вектор  направлен перпендикулярно отрезку
направлен перпендикулярно отрезку 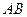 в сторону вращения, если оно ускоренное (рис. 103,а) или против вращения, если оно замедленное (рис. 103, б).
в сторону вращения, если оно ускоренное (рис. 103,а) или против вращения, если оно замедленное (рис. 103, б).
Пример №17.
Для механизма, изображенного на рис. 104, определить ускорение ползуна  и точки
и точки 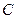 , если колесо
, если колесо 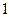 радиуса
радиуса 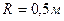 катится с постоянной скоростью его центра
катится с постоянной скоростью его центра 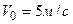 , угол
, угол  ,
, 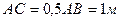 .
.
 Решение:
Решение:
1. Колесо катится по горизонтальной поверхности с постоянной скоростью его центра, т.е. 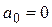 .
.
Выразим ускорение точки 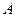 , принимая за полюс точку
, принимая за полюс точку 
 , (1)
, (1)
где 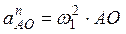 ,
, 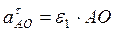 ;
;
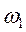 и
и 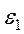 - соответственно угловая скорость и угловое ускорение колеса.
- соответственно угловая скорость и угловое ускорение колеса.
Так как центр колеса движется с постоянной скоростью, то 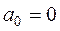 ,
, 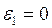 . Следовательно,
. Следовательно,
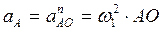 .
.
Угловую скорость колеса найдем, принимая во внимание, что мгновенный центр колеса находится в точке  касания его с неподвижной поверхностью. Тогда
касания его с неподвижной поверхностью. Тогда
 ;
;
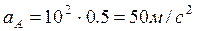 .
.
2. Определим ускорение точки  , принимая за полюс точку
, принимая за полюс точку  :
:
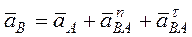 . (2) В векторном равенстве (2) для вектора
. (2) В векторном равенстве (2) для вектора 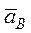 ускорение точки
ускорение точки  известно направление, так как ползун
известно направление, так как ползун  движется в горизонтальных направляющих. Предполагаем, что вектор
движется в горизонтальных направляющих. Предполагаем, что вектор 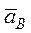 направлен по горизонтали вправо. Вектор ускорения точки
направлен по горизонтали вправо. Вектор ускорения точки 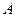 (полюса) известен по модулю и направлению. Определим нормальную составляющую ускорения звена
(полюса) известен по модулю и направлению. Определим нормальную составляющую ускорения звена 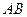 во вращательном движении вокруг полюса:
во вращательном движении вокруг полюса: 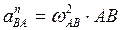 ,
,
где  - угловая скорость звена
- угловая скорость звена 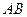 .
.
Так как векторы скоростей 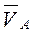 и
и 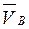 точек
точек 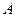 и
и  звена
звена 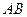 параллельны между собой (рис. 104), мгновенный центр скоростей звена
параллельны между собой (рис. 104), мгновенный центр скоростей звена 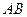 находится в бесконечности, т.е. звено
находится в бесконечности, т.е. звено 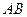 совершает мгновенно поступательное движение. Следовательно,
совершает мгновенно поступательное движение. Следовательно,
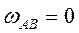 ,
, 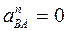 .
.
Выразим касательную составляющую ускорения:
 .
.
Численное значение углового ускорения звена 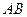 неизвестно. Вектор
неизвестно. Вектор 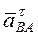 направлен перпендикулярно составляющей
направлен перпендикулярно составляющей 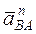 .
.
В векторном равенстве (2) неизвестны численные значения ускорений 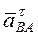 ,
, 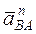 .
.
Для их нахождения спроецируем (2) на две взаимно перпендикулярные оси координат 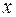 и
и 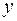 , направляя ось
, направляя ось 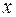 вдоль звена
вдоль звена 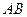 :
:
на ось 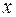 :
: 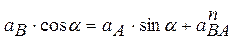 ; (3)
; (3)
на ось у: 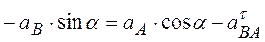 . (4)
. (4)
Из уравнения (3) с учетом того, что 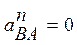 , получим
, получим 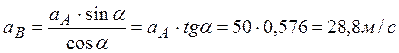 .
.
Из уравнения (4) определим составляющую 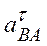 :
:
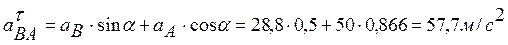
Угловое ускорение звена 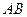 :
:
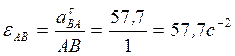 .
.
3. Выразим ускорение точки 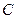 , принимая за полюс точку
, принимая за полюс точку 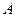 .
. 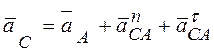 . (5)
. (5)
Определим предварительно величину составляющих 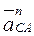 ,
, 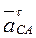 :
:
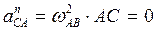 ,
,
так как 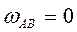 ;
;
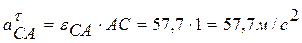
Так как ускорение точки 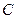 неизвестно ни по модулю, ни по направлению, определим его по проекциям на координатные оси. Для этого необходимо спроецировать векторное уравнение (5) на координатные оси.
неизвестно ни по модулю, ни по направлению, определим его по проекциям на координатные оси. Для этого необходимо спроецировать векторное уравнение (5) на координатные оси.
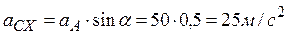 ;
;
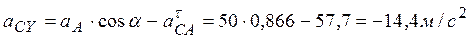 ;
;
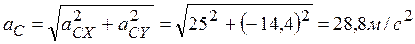 .
.
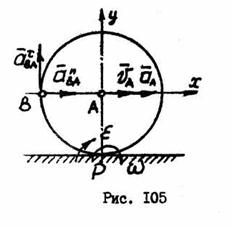
Пример №18.
Колесо радиуса 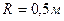 катится без скольжения по горизонтальной поверхности (рис. 105), имея в данный момент времени скорость центра VA=1м/с и ускорение аА=2м/с2. Определить скорость и ускорение точки В.
катится без скольжения по горизонтальной поверхности (рис. 105), имея в данный момент времени скорость центра VA=1м/с и ускорение аА=2м/с2. Определить скорость и ускорение точки В.
Решение:
 1. Выразим ускорение точки
1. Выразим ускорение точки  , принимая за полюс точку
, принимая за полюс точку 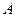 :
:
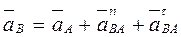 . (1)
. (1)
Так как направление вектора ускорения точки  неизвестно, необходимо определить численные значения всех слагаемых правой части векторного уравнения (1).
неизвестно, необходимо определить численные значения всех слагаемых правой части векторного уравнения (1).
Выразим касательную и нормальную составляющие ускорения 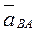 :
:
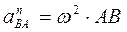 ;
; 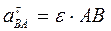 ,
,
где 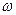 ,
, 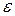 - соответственно угловая скорость и угловое ускорение колеса.
- соответственно угловая скорость и угловое ускорение колеса.
Угловую скорость колеса определим, зная скорость точки  и положение мгновенного центра скоростей колеса – точки
и положение мгновенного центра скоростей колеса – точки 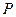 :
:  .
.
Угловое ускорение колеса определим как производную по времени от угловой скорости колеса: 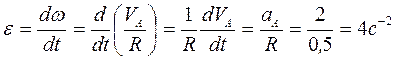 ;
;
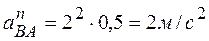 ;
;
Дата публикования: 2014-10-20; Прочитано: 721 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
