ВВЕДЕНИЕ 4 страница. 2. Можно было рассмотреть пластину , и из нее вычесть два выреза и .

2. Можно было рассмотреть пластину , и из нее вычесть два выреза и .

Тогда

;

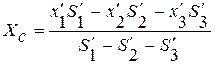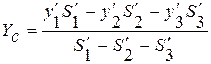
Центры тяжести некоторых однородных тел.

Центр тяжести дуги окружности в силу симметрии лежит на оси

симметрии (рис.49) и имеет координату:

, (20.4)

где - угол, измеряемый в радианах.

Центр тяжести площади кругового сектора лежит на оси

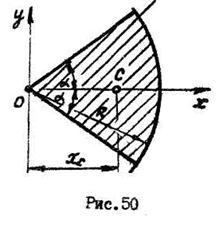симметрии (рис.50) и имеет координату:

. (20.5)

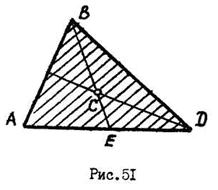
Центр тяжести треугольника лежит в точке пересечения медиан:

.

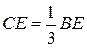Пример №12.

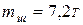Определить положение центра тяжести автокрана и статические нагрузки на его передний и задний спаренные колесные хода, если общая масса автокрана , масса шасси ; масса стрелы 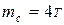; кабины крановщика с поворотным устройством . Размеры приведены на рис.52а.

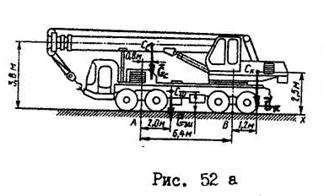Решение:

Данные для определения координат центра тяжести сведены в табл. 2.

Элемент	Масса 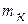,	Координаты центра тяжести
,	,
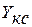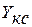
Кабина крановщика с поворотным устройством	4,8	7,6	2,5	36,48	12,0
Шасси	7,2	2,0	1,4	14,4	10,08
Стрела	4,0	0,8	3,8	3,2	15,2
Сумма	16,0			54,08	37,28

;

.

Для определения статических нагрузок на передний и задний спаренные колесные хода составим расчетную схему (рис.52б). Для плоской системы параллельных сил составим два уравнения равновесия:

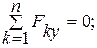
(1)

(2)

Тогда

из (2):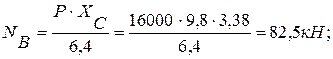

из (1):

2. К И Н Е М А Т И К А

2.1. ПРЕДМЕТ И ЗАДАЧИ КИНЕМАТИКИ.

Кинематика - раздел механики, который изучает геометричес­кие свойства механического движения тел без учета их массы и причин, вызывающих движение. Под механическим движением понима­ется происходящее с течением времени перемещение точек и тел в пространстве. При движении твердого тела его точки могут дви­гаться различно, поэтому изучение кинематики начинается с изу­чения-движения самого простого объекта - материальной точки.

Положение точки в пространстве определяется относительно системы отсчета, за которую может быть принято какое-то твердое тело и связанная с ним система координат.

Задачи, решаемые методами кинематики точки, можно разде­лить на следующие типы:

1) определение траектории движения точки;

2) определение скорости и ускорения точки по заданному закону
движения - прямая задача кинематики;

3) определение закона движения точки в выбранной системе отсче­та - обратная задача кинематики.

СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ.

Определить движение точки - это значит определить положе­ние этой точки в любой момент времени по отношению к выбранной системе отсчета.

Кривая, которую описывает точка при своем движении в про­странстве относительно выбранной системы отсчета, называется траекторией (рис. 53,54).

Движение точки можно задать векторным, координатным и естественным способами.

При векторном способе положение точки задается радиусом - вектором , проведенным из некоторой неподвижной точки О (рис. 55). Каждому моменту времени соответствует новое значение радиуса – вектора . Следовательно, для векторного способа задания движения уравнение движения точки имеет вид:

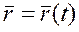(2.1)

В декартовой системе координат 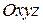(рис.56) положение точки определяется тремя ее координатами, изменяющимися во времени. Тогда в координатной форме уравнения движения точки будут иметь следующий вид:

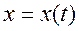, , (2.2)

Если точка движется в плоскости , будем иметь два уравнения движения:

, (2.3)

При прямолинейном движении точки прямую, по которой движется точка принимаем за ось координат. Уравнение движения точки имеет вид:

. (2.4)

Между векторным и координатным способами задания движения су­ществует непосредственная связь. Координаты точки являются проекциями на оси координат, ее радиуса-вектора , а сам ра­диус-вектор можно определить через его проекции на координат­ные оси:

, (2.5)

где 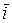, , 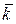- орты координатных осей , , .

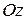Естественный способ задания движения точки используется, если точка движется по криволинейной траектории (рис. 57). В этом случае для точки должны быть известны траектория движения, начало отсчета, направление отсчета.

Принимая за начало отсчета точку 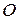и выбрав положительное нап­равление отсчета, положение точки в любой момент времени можно определить дуговой координатой ,которая изменяется с течением времени (рис.58).

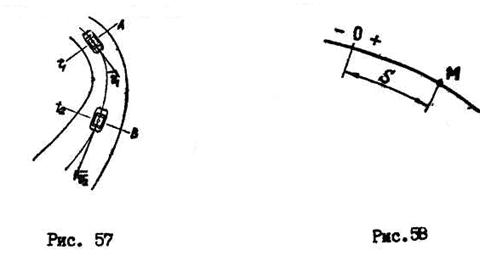
Уравнение движения точки в естественной форме будет иметь вид:

. (2.6)

Взаимосвязь между координатным и естественным способами задания движения точки можно установить через дифференциал дуговой координаты:

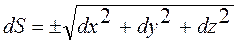, (2.7)

где 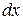, , - дифференциалы координат точек;

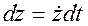, , (2.8)

После интегрирования (2.7) в интервале времени от 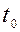до 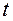получим:

(2.9)

Знак плюс соответствует движению в положительном направлении отсчета дуговой координаты, знак минус – положительному направлению. В формулах (2.8) и (2.9)

, , - производные по времени от соответствующих координат (см. формулы 2.13).

ОПРЕДЕЛЕНИЕ ТРАЕКТОРИИ ДВИЖЕНИЯ ТОЧКИ.

Пример №1.

Кривошип вращается с постоянной угловой скоростью . Найти траекторию движения средней точки шатуна, если 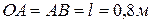. В начальный момент времени ползун находиться в крайнем правом положении. Начало координат поместить в точку .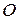

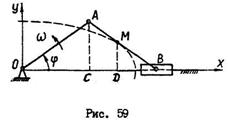
Положение механизма определяется углом поворота ведущего звена – кривошипа , изменяющимся во времени по закону .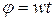

В выбранной системе отсчета выразим координаты точки :

. (1)

С учетом исходных данных уравнения (1) примут вид:

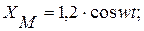
. (2)

Уравнения (2) определяет закон движения точки . Для нахождения уравнения траектории из уравнений движения необходимо исключить параметр :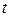

, .

Возведем в квадрате и сложим:

.

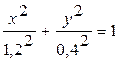Следовательно, средняя точка шатуна движется по замкнутой эллиптической траектории с центром в точке 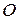и полуосям:

, .

2.3. СКОРОСТЬ ТОЧКИ.

Скоростью точки называется векторная величина, характеризующая быстроту и направление движения точки в пространстве. При векторном способе задания движения скорость определяется первой производной радиуса-вектора по времени:

(2.10)

Вектор скорости можно выразить через его проекции на координатные оси.

(2.11)

При координатном способе задания движения точки модуль скорости определяется по проекциям вектора скорости на оси декартовых координат:

, (2.12)

где ,

,

. (2.13)

Направление вектора-скорости можно найти через направляющие косинусы углов, которые вектор скорости точки составляет с координатными осями:

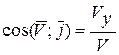, , . (2.14)

При естественном способе задания движения точки вектор скорости определяется формулой:

, (2.15)

где 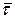- единичный вектор (орт) касательной, направленный в сторону возрастающих значений дуговой координаты (рис.60).

Алгебраическую величину скорости точи определяются по формуле:

, (2.16)

Если 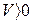, точка движется в сторону возрастающих, а при 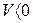в сторону убывающих значений дуговой координаты.

УСКОРЕНИЕ ТОЧКИ.

Ускорением точки называется векторная величина, характеризующая быстроту изменения во времени скорости движения.

При векторном способе задания движения точки вектор ускорения определяется первой производной по времени от вектора скорости или второй производной по времени от радиуса-вектора:

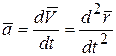. (2.17)

Вектор ускорения точки можно выразить через проекции на оси декартовых координат:

, (2.18)

где ;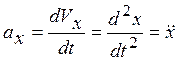

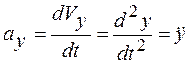; (2.19)

.

Модуль ускорения точки определяется выражением:

. (2.20)

Направление вектора ускорения точки в пространстве можно определить через направляющие косинусы:

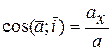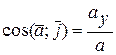, , . (2.21)

ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПО ЗАДАННОМУ ЗАКОНУ ДВИЖЕНИЯ.

Решение первой задачи кинематики рекомендуется осуществлять в такой последовательности:

а) выбрать систему координат;

б) записать уравнения движения в выбранной системе координат;

в) по уравнениям движения определить проекции скорости на оси координат, модуль и направление вектора скорости;

г) определить модуль и направление вектора ускорения по проекциям на координатные оси.

Пример №2. Координатный способ задания движения точки.

По заданным уравнениям движения точки 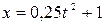, 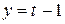(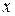, 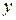- в метрах, 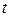- в секундах) определить для момента времени скрость и ускорение, радиус кривизны траектории движения точки.

Решение:

1. Для определения уравнения траектории точки исключим из заданных уравнений движения параметр :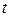

, .

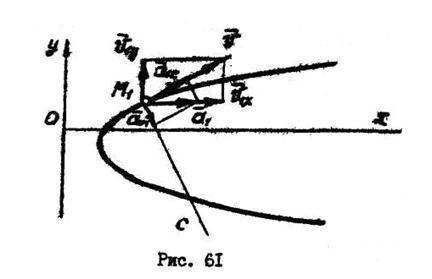
Следовательно, траекторией движения точки будет парабола (рис.61). В заданный момент времени точка имеет координаты:

, .

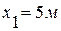2. Скорость точки найдем по проекциям на координатные оси:

, ,

.

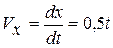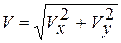При

; ;

.

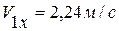3. Аналогично найдем ускорение точки:

; ; .

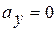4. Радиус кривизны траектории можно найти по формуле:

.

Ускорение точки можно выразить через проекции на естественные оси координат:

,

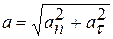где 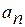, - соответственно нормальная и касательная составляющие ускорения.

Так как величина ускорения для заданного момента времени уже определена, можно выразить нормальное ускорение:

.

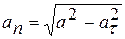Касательное ускорение найдем, дифференцируя по времени равенство:

.

Получим

или

.

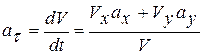Для заданного момента времени:

;

;

.

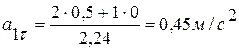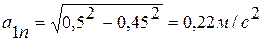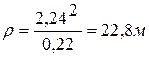При естественном способе задания движения точки ускорение точки определяется по проекциям на естественные оси координат. Пусть точка движется по криволинейной траектории (рис. 62).

Построим с началом в точке естественную систему координат: ка­сательную , нормаль и бинормаль 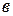. Орт касательной направлен в сторону возрастания дуговой координаты (в положительном направлении).
Нормаль перпендикулярна касательной. Орт нормали 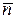направлен к центру кривизны траектории, в сторону вогнутости траек­тории и определяет положительное направление второй естественной оси.

Бинормаль 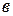перпендикулярна нормали и касательной. Еди­ничный вектор бинормали направлен так, чтобы три вектора

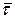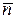, , образовали правую систему координат.

При движении точки по криволинейной траектории естественные оси изменяют свое положение в пространстве, т.е. орты 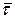, , 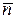также изменяют свое направление в пространстве (явля­ются переменными). Вектор ускорения лежит в плоскости, проходя­щей через касательную и нормаль. Дифференцируя (2.15) по време­ни, выразим вектор ускорения через проекции на естественные оси:

(2.22)

где

- касательное или тангенциальное ускорение, проекция век­тора ускорения на касательную, характеризует изменение скорости по величине, может иметь положительное или отрицательное значение (рис. 63):

. (2.23)

Нормальное ускорение является проекцией вектора ускорения на нормаль, характеризует изменение скорости по направлению. Величина нормального ускорения всегда положительна (рис. 63) и определяется формулой:

, (2.24)

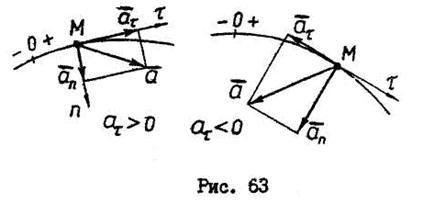
где 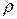- радиус кривизны траектории.

Модуль ускорения можно определить по проекциям на естественные оси координат.

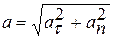. (2.25)