 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
ВВЕДЕНИЕ 9 страница. Дуге соответствует центральный угол
|
|
 .
.
Дуге 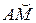 соответствует центральный угол:
соответствует центральный угол:
 .
.
По условию задачи задано положительное направление отсчета относительной координаты 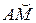 . Так как дуговая координата
. Так как дуговая координата 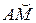 и соответствующий ей угол получены с отрицательными знаками, откладываем угол
и соответствующий ей угол получены с отрицательными знаками, откладываем угол  в отрицательном направлении.
в отрицательном направлении.
3. Выразим абсолютную скорость точки:
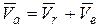 , (1)
, (1)
где 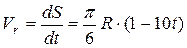 ,
,
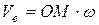 .
.
Так как 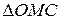 -равносторонний,
-равносторонний,  .
.
В заданный момент времени:
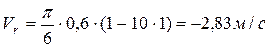 ,
,
 .
.
Вектор 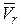 относительной скорости направлен в соответствии с полученным знаком. Значение абсолютной скорости точки
относительной скорости направлен в соответствии с полученным знаком. Значение абсолютной скорости точки  определим по проекциям на координатные оси:
определим по проекциям на координатные оси:
 ;
;
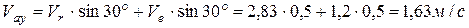 ;
;
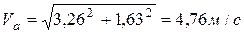 .
.
4. Абсолютное ускорение точки определим по теореме Кориолиса:
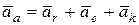 . (2)
. (2)
Так как в переносном и относительном движении точка движется неравномерно по криволинейным траекториям, уравнение (2) примет вид:
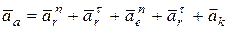 (3)
(3)
Вычислим слагаемые абсолютного ускорения:
 ,
,
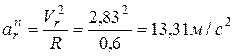 .
.
Совпадение знаков относительной скорости и касательной составляющей относительного ускорения показывает, что относительное движение точки является ускоренным.
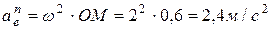 ,
,
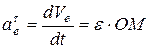 .
.
Так как диск вращается с постоянной угловой скоростью, то 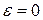 .
.
Ускорение Кориолиса:
 .
.
Модуль абсолютного ускорения определим, проецируя векторное равенство (3) на координатные оси:
 ;
;
 ;
;
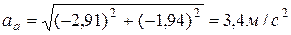 .
.
Пример №24.
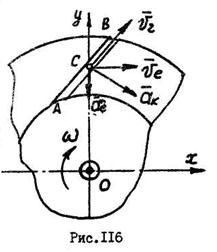
Рабочее колесо компрессора с прямолинейными каналами (рис.116) равномерно вращается с угловой скоростью  вокруг оси
вокруг оси 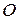 , перпендикулярной плоскости чертежа. Воздух течет по каналам с постоянной относительной скоростью
, перпендикулярной плоскости чертежа. Воздух течет по каналам с постоянной относительной скоростью 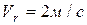 . Найти абсолютную скорость и абсолютное ускорение для частицы воздуха, находящейся в точке
. Найти абсолютную скорость и абсолютное ускорение для частицы воздуха, находящейся в точке 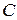 канала
канала  , наклоненного под углом
, наклоненного под углом  , если
, если 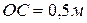 .
.
 Решение:
Решение:
1. Определим абсолютную скорость точки по теореме о сложении скоростей:
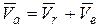 , (1)
, (1)
где 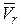 - относительная скорость движения частицы воздуха по каналу
- относительная скорость движения частицы воздуха по каналу  ;
;
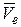 - переносная скорость, т.е. скорость точки
- переносная скорость, т.е. скорость точки 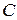 канала
канала  , в которой в данный момент времени находится частица воздуха.
, в которой в данный момент времени находится частица воздуха.
 .
.
Модуль абсолютной скорости определим, проецируя векторное равенство (1) на координатные оси:
 ,
,
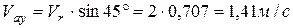 ,
,
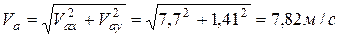 .
.
2. Определим абсолютное ускорение точки по теореме Кориолиса:
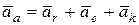 (2)
(2)
Относительное ускорение 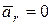 , так как по условию задачи частица воздуха движется по каналу
, так как по условию задачи частица воздуха движется по каналу  с постоянной скоростью:
с постоянной скоростью:
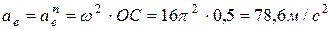 .
.
Ускорение Кориолиса:
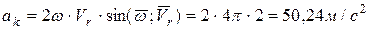 .
.
Спроецируем векторное равенство (2) на координатные оси:
 ,
,
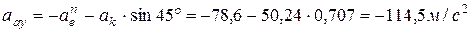 ,
,
 .
.
Пример №25.
Кулисный механизм состоит из двух параллельных валов 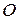 и
и 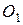 , кривошипа
, кривошипа  и кулисы
и кулисы 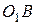 (рис.117). Кривошип
(рис.117). Кривошип  вращается равномерно вокруг оси
вращается равномерно вокруг оси 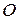 с постоянной угловой скоростью
с постоянной угловой скоростью 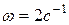 . Камень
. Камень  перемещается вдоль прорези кулисы
перемещается вдоль прорези кулисы 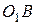 . Найти угловую скорость и угловое ускорение кулисы в момент времени, когда угол поворота кривошипа
. Найти угловую скорость и угловое ускорение кулисы в момент времени, когда угол поворота кривошипа 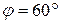 , если расстояние между осями валов
, если расстояние между осями валов 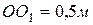 .
.
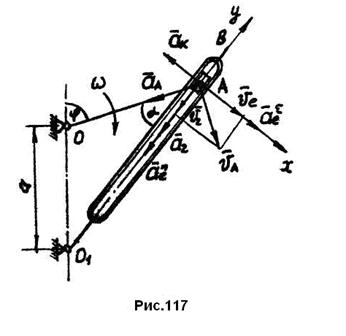
Решение:
1. Абсолютным движение точки  является вращение вместе с кривошипом
является вращение вместе с кривошипом  вокруг оси
вокруг оси 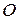 с угловой скоростью
с угловой скоростью  :
:
 .
.
Вектор абсолютной скорости можно разложить на две составляющие: вектор 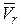 относительной скорости точки
относительной скорости точки  вдоль прорези кулисы и вектор
вдоль прорези кулисы и вектор 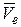 переносной скорости вращения кулисы
переносной скорости вращения кулисы 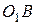 вокруг оси
вокруг оси 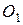 , тогда:
, тогда:
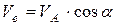 ,
, 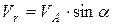 .
.
Так как 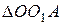 равнобедренный,
равнобедренный, 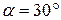 , т.е.
, т.е.
 ,
,
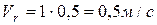 .
.
Так как переносным движением для точки  является вращение кулисы вокруг оси
является вращение кулисы вокруг оси 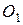 , а величина переносной скорости
, а величина переносной скорости 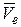 определена, можно найти угловую скорость кулисы:
определена, можно найти угловую скорость кулисы:
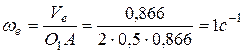 .
.
2. Определим абсолютное ускорение точки:
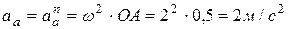 .
.
Выразим абсолютное ускорение точки  по теореме Кориолиса:
по теореме Кориолиса:
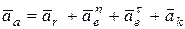 , (1)
, (1)
где 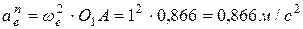 ,
,
 ; (2)
; (2)
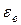 - угловое ускорение кулисы.
- угловое ускорение кулисы.
Вычислим ускорение Кориолиса:
 .
.
Для нахождения углового ускорения 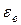 кулисы спроецируем векторное равенство (1) на ось
кулисы спроецируем векторное равенство (1) на ось 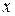 :
:
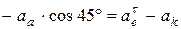 ;
;
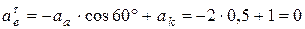 .
.
Учитывая соотношение (2), найдем угловой ускорение кулисы:
 .
.
т.е кулиса 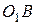 вращается с постоянной угловой скоростью
вращается с постоянной угловой скоростью 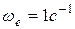 .
.
Пример №26.
По радиусу диска (рис.118), вращающегося вокруг вертикальной оси 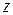 с угловой скоростью
с угловой скоростью  в направлении от центра диска к ободу по закону
в направлении от центра диска к ободу по закону 
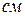 , движется точка
, движется точка  . Радиус
. Радиус 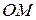 составляет с осью вращения угол
составляет с осью вращения угол 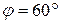 . Определить величину абсолютного ускорения точки в момент
. Определить величину абсолютного ускорения точки в момент  .
.

Решение:
1. Абсолютное ускорение точки можно определить по теореме Кориолиса:
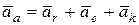 (1)
(1)
Зная закон относительного движения, можно найти относительное ускорение точки:
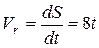 ;
;
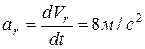 .
.
В переносном движении точка  движется по окружности радиуса
движется по окружности радиуса 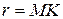 , поэтому:
, поэтому:
 ;
;
 ;
;
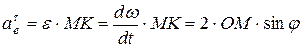 .
.
Ускорение Кориолиса:
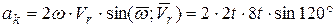 .
.
Направление вектора ускорения Кориолиса определим по правилу Жуковского: перенесем в точку  вектор
вектор 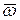 угловой скорости переносного вращательного движения, спроецируем вектор
угловой скорости переносного вращательного движения, спроецируем вектор 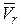 на горизонтальную плоскость, перпендикулярную вектору
на горизонтальную плоскость, перпендикулярную вектору 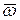 , и повернем проекцию на
, и повернем проекцию на 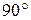 в сторону вращения, т.е. вектор
в сторону вращения, т.е. вектор  направлен в сторону, противоположную положительному направлению оси
направлен в сторону, противоположную положительному направлению оси 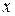 .
.
Для заданного момента времени  :
:
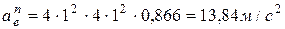 ;
;
 ;
;
 .
.
Вычислим абсолютное ускорение точки по проекциям на координатные оси:
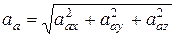 ;
;
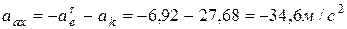 ;
;
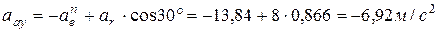 ;
;
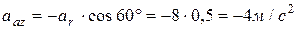 ;
;
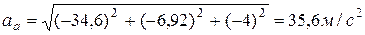 .
.
2.10. ВРАЩЕНИЕ ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ.
Всякое элементарное перемещение тела, имеющего неподвижную точку (рис.119), представляет собой элементарный поворот вокруг некоторой мгновенной оси вращения 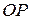 , проходящей черев эту точку.
, проходящей черев эту точку.
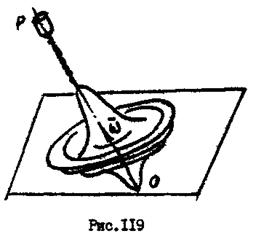 Скорости всех точек, лежащих на мгновенной оси вращения, равны нулю. Положение мгновенной оси вращения в пространстве и в самом теле постоянно изменяется.
Скорости всех точек, лежащих на мгновенной оси вращения, равны нулю. Положение мгновенной оси вращения в пространстве и в самом теле постоянно изменяется.
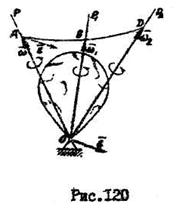
Вектор 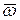 мгновенной угловой скорости направлен вдоль мгновенной оси вращения. Со временем вектор мгновенной угловой скорости изменяется как по величине, так и по направлению (рис.120). Мгновенное угловое ускорение определяет изменение угловой скорости
мгновенной угловой скорости направлен вдоль мгновенной оси вращения. Со временем вектор мгновенной угловой скорости изменяется как по величине, так и по направлению (рис.120). Мгновенное угловое ускорение определяет изменение угловой скорости 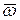 по величине и направлении:
по величине и направлении:
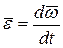 (2.53)
(2.53)
Вектор мгновенного углового ускорения направлен по касательной к кривой 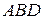 , являющейся годографом вектора мгновенной угловой скорости.
, являющейся годографом вектора мгновенной угловой скорости.
Скорость любой точки тела пропорциональна расстоянию 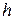 этой точки до мгновенной оси вращения (рис.121)
этой точки до мгновенной оси вращения (рис.121) 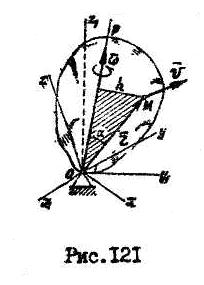 :
:
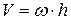 , (2.54)
, (2.54)
где  - мгновенная скорость колеса;
- мгновенная скорость колеса;
 - радиус-вектор, определяющий положение точки
- радиус-вектор, определяющий положение точки  относительно неподвижной точки
относительно неподвижной точки 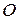 .
.
Ускорение точ5ки состоит из вращательной 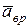 и осестремительной
и осестремительной 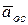 составляющих:
составляющих:
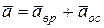 , (2.55)
, (2.55)
 ,
, 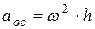 , (2.56)
, (2.56)
где 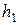 - расстояние от точки
- расстояние от точки  до вектора
до вектора 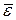 ;
;
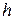 - расстояние от точки
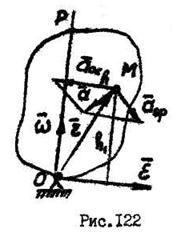
- расстояние от точки  до мгновенной оси вращения (рис.122).
до мгновенной оси вращения (рис.122).
Вектор 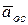 осестремительного ускорения направлен перпендикулярно мгновенной оси вращения. Вектор
осестремительного ускорения направлен перпендикулярно мгновенной оси вращения. Вектор 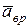 вращательного ускорения направлен перпендикулярно плоскости, проходящей через точку
вращательного ускорения направлен перпендикулярно плоскости, проходящей через точку  и вектор
и вектор  .
.
Пример №27.
Найти скорости точек  и
и 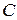 конического катка (бегуна), катящегося без скольжения по горизонтальной конической опоре, если точка
конического катка (бегуна), катящегося без скольжения по горизонтальной конической опоре, если точка 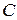 лежит на окружности радиуса
лежит на окружности радиуса 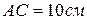 , расстояние
, расстояние 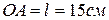 . Скорость движения центра
. Скорость движения центра  катка по его траектории постоянна и равна
катка по его траектории постоянна и равна 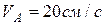 (рис.123).
(рис.123).
Решение:
1. Мгновенная ось вращения проходит через две неподвижные точки 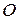 и
и  . Сферическое движение катка можно рассматривать как вращение вокруг мгновенной оси
. Сферическое движение катка можно рассматривать как вращение вокруг мгновенной оси 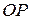 . Скорость любой точки тела при таком движении пропорциональна расстоянию до мгновенной оси вращения. Так как скорость точки
. Скорость любой точки тела при таком движении пропорциональна расстоянию до мгновенной оси вращения. Так как скорость точки  известна, можно определить
известна, можно определить
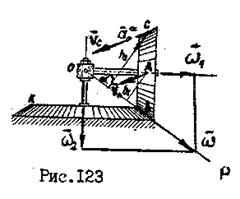 мгновенную угловую скорость:
мгновенную угловую скорость:
 ,
,
где 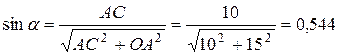 ;
; 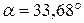 .
.
2. Определим угловую скорость собственного вращения катка 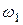 , которая является угловой скоростью относительного движения:
, которая является угловой скоростью относительного движения:
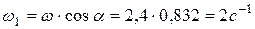 .
.
Каток участвует в переносном вращательном движении вокруг оси 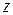 с угловой скоростью
с угловой скоростью 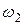 .
.
Определим скорость точки 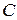 :
:
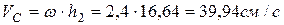 ;
;
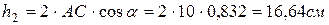 .
.
Скорость точки  равна нулю, так как точка находится на мгновенной оси вращения.
равна нулю, так как точка находится на мгновенной оси вращения.
3.Ускорение точки 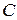 состоит из вращательной и осестремительной составляющих:
состоит из вращательной и осестремительной составляющих:
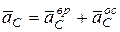 (1)
(1)
где 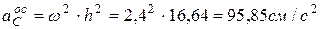 .
.
Вектор 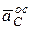 направлен перпендикулярно мгновенной оси вращения по отрезку, составляющему
направлен перпендикулярно мгновенной оси вращения по отрезку, составляющему  .
.
2.11. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО
ТВЕРДОГО ТЕЛА.
Свободное твердое тело имеет 6 степеней свободы и может перемещаться как угодно в пространстве по отношению к некоторой
неподвижной системе отсчета.
 Любое элементарное перемещение свободного твердого тела слагается из элементарного поступательного перемещения вместе с полюсом
Любое элементарное перемещение свободного твердого тела слагается из элементарного поступательного перемещения вместе с полюсом  и элементарного поворота вокруг мгновенной оси вращения
и элементарного поворота вокруг мгновенной оси вращения  , проходящей через этот полюс (рис.124). Любая точка тела участвует в сложном движении: относительном вращательном движении вместе с телом вокруг полюса
, проходящей через этот полюс (рис.124). Любая точка тела участвует в сложном движении: относительном вращательном движении вместе с телом вокруг полюса  и в переносном поступательном движении вместе с полюсом
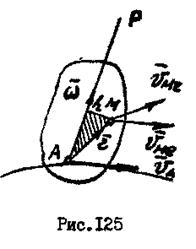
и в переносном поступательном движении вместе с полюсом  . Скорость точки определяется геометрической суммой (рис.125):
. Скорость точки определяется геометрической суммой (рис.125):
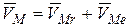 , (2.57)
, (2.57)
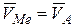
 ,
,
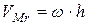 ,
,
где 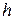 - расстояние до мгновенной оси вращения;
- расстояние до мгновенной оси вращения;
Ускорение точки  также определяется геометрической суммой:
также определяется геометрической суммой:
 , (2.58)
, (2.58)
Где 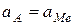 ,
,
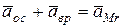 .
.
2.12. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА.
Движение тела называется сложным, если тело движется от-нисительно подвижной системы отсчета, которая, в свою очередь, совершает переносное движение по отношению к неподвижной системе отсчета.
 При сложении двух поступательных движений результирующее движение тела так же является поступательным со скоростью, равной геометрической сумме скоростей составляющих движений:
При сложении двух поступательных движений результирующее движение тела так же является поступательным со скоростью, равной геометрической сумме скоростей составляющих движений:
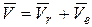 (2.59)
(2.59)
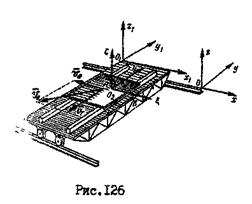
Тележка крана  (рис. 126) движется поступательно со скоростью
(рис. 126) движется поступательно со скоростью 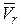 относительно подвижной системы отсчета
относительно подвижной системы отсчета 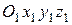 . Подвижная система отсчета жестко связана с фермой крана, которая со скоростью
. Подвижная система отсчета жестко связана с фермой крана, которая со скоростью 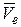 совершает поступательное движение относительно неподвижной системы отсчета
совершает поступательное движение относительно неподвижной системы отсчета 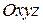 . Результирующее движение тележки также является поступательным со скоростью
. Результирующее движение тележки также является поступательным со скоростью 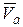 .
.
При сложении двух вращательных движений вокруг вертикальных осей возможны три частных случая:
1. Вращения направлены в одну сторону. Если тело участвует одновременно в двух направленных в одну сторону вращениях вокруг параллельных осей, то его результирующее движение будет мгновенным вращением с абсолютной угловой скоростью, равной сумме угловых скоростей составляющих вращений, вокруг мгновенной оси, параллельной осям составляющих вращений.
 Колесо 2 (рис.127) обкатывается по неподвижному колесу
Колесо 2 (рис.127) обкатывается по неподвижному колесу 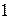 вследствие вращения кривошипа
вследствие вращения кривошипа  с угловой скоростью
с угловой скоростью 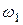 вокруг оси
вокруг оси 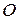 . Одновременно колесо
. Одновременно колесо  вращается вокруг собственной оси
вращается вокруг собственной оси  с угловой скоростью
с угловой скоростью 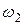 . Направления двух вращений совпадают. Результирующим движением для колеса
. Направления двух вращений совпадают. Результирующим движением для колеса  является вращение вокруг мгновенной оси, проходящей через мгновенный центр скоростей - точку
является вращение вокруг мгновенной оси, проходящей через мгновенный центр скоростей - точку  , с угловой скоростью:
, с угловой скоростью:
Дата публикования: 2014-10-20; Прочитано: 551 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
