 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
ВВЕДЕНИЕ 8 страница. Спроецируем векторное равенство (1) на координатные оси х и у:
|
|
 .
.
Спроецируем векторное равенство (1) на координатные оси х и у:  ;
;
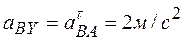 ;
;
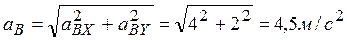 .
.
Пример №19.
Для плоского механизма, состоящего из стержней 1, 2, 3, 4 и ползуна  , соединенных между собой и с опорами О1 и О2 шарнирно, положение механизма определяется углами
, соединенных между собой и с опорами О1 и О2 шарнирно, положение механизма определяется углами  ,
,  ,
,  ,
, 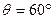 (рис. 106).
(рис. 106).
 Ведущее звено – кривошип ОА вращается с постоянной угловой скоростью
Ведущее звено – кривошип ОА вращается с постоянной угловой скоростью  . Определить скорость точки
. Определить скорость точки  , угловую скорость и угловое ускорение звена
, угловую скорость и угловое ускорение звена 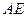 , если размеры звеньев механизма
, если размеры звеньев механизма 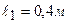 ,
,  ,
,  ,
, 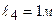 ,
, 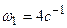 .
.
Решение:
1. Определим скорость точки 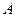 кривошипа
кривошипа  :
: 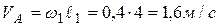 .
.
Для звена 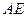 известны направления скоростей
известны направления скоростей 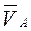 и
и 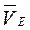 точек
точек 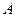 и
и 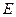 , принадлежащих одновременно вращающимся звеньям
, принадлежащих одновременно вращающимся звеньям  и
и 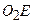 . Мгновенный центр скоростей звена
. Мгновенный центр скоростей звена 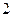 находится на пересечении перпендикуляров, проведенных к векторам
находится на пересечении перпендикуляров, проведенных к векторам 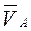 и
и 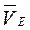 . для точек
. для точек 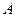 ,
,  ,
, 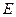 звена
звена 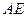 запишем соотношения:
запишем соотношения:
 ;
;
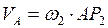 ;
;
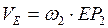 .
.
Так как 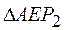 - равносторонний,
- равносторонний, 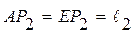 , следовательно,
, следовательно,
 ;
;
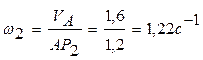 ;
;
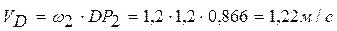 .
.
Вектор  скорости точки D направлен перпендикулярно отрезку
скорости точки D направлен перпендикулярно отрезку  , являющемуся высотой
, являющемуся высотой  .
.
2. Скорость ползуна  и угловую скорость звена 3 определим с помощью мгновенного центра скоростей звена 3, который находится в точке Р3. Запишем соотношения для звена 3:
и угловую скорость звена 3 определим с помощью мгновенного центра скоростей звена 3, который находится в точке Р3. Запишем соотношения для звена 3:
 .
.
Из  выразим
выразим 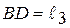 ;
; 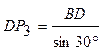 ;
;
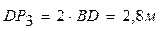 ;
;
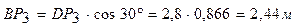 ;
;
 ;
;
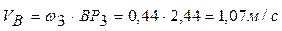 .
.
3. Так как кривошип О1А вращается с постоянной угловой скоростью, ускорение точки 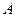 определим по формуле:
определим по формуле: 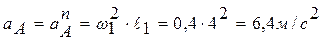 .
.
Принимая точку 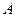 за полюс, выразим ускорение точки
за полюс, выразим ускорение точки 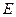 :
:
 . (1)
. (1)
Так как точка 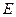 принадлежит звену
принадлежит звену 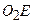 , вращающемуся вокруг оси
, вращающемуся вокруг оси 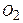 , ускорение точки
, ускорение точки 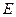 состоит из нормальной и касательной составляющих:
состоит из нормальной и касательной составляющих:
 . (2)
. (2)
Ускорение звена АЕ во вращательном движении состоит из двух слагаемых:
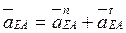 . (3)
. (3)
С учетом (2) и (3) векторное равенство (1) примет вид:
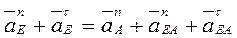 (4)
(4)
Выразим слагаемые векторного равенства (4):
 ;
;
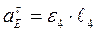 ;
;
 ;
;
 .
.
В векторном равенстве (4) слагаемые  и
и 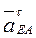 известны только по направлению. Для нахождения двух неизвестных величин спроецируем (4) на две координатные оси, направляя ось х вдоль звена
известны только по направлению. Для нахождения двух неизвестных величин спроецируем (4) на две координатные оси, направляя ось х вдоль звена 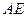 , а ось у – перпендикулярно звену:
, а ось у – перпендикулярно звену:
на ось х:  , (5)
, (5)
на ось у: 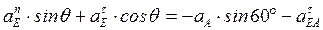 , (6)
, (6)
из (5) 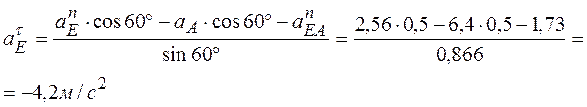

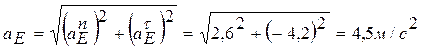 .
.
Знак (-) показывает, что направление вектора 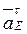 противоположно показанному на чертеже.
противоположно показанному на чертеже.
Из (6):

Зная ускорение  , найдем угловое ускорение звена 2:
, найдем угловое ускорение звена 2: 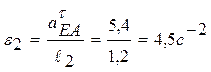 .
.
2.9. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ.
В ряде случаев движение точки можно рассматривать по отношению к двум системам отсчета, из которых одну можно считать условно неподвижной. Например, движение человека по движущейся лодке (рис. 107) по отношению к берегу является сложным, состоящим из движения относительно лодки (подвижная система отсчета) и движение вместе с лодкой по отношению к берегу (неподвижная система отсчета).
Движение точки относительно неподвижной системы отсчета называется абсолютным движением. Движение точки относительно подвижной системы отсчета называется относительным. Движение точки вместе с подвижной системой отсчета относительно неподвижной системы отсчета является для точки переносным.
 При сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей.
При сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей.
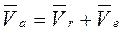 , (2.40)
, (2.40)
где  - абсолютная скорость точки в движении относительно неподвижной системы отсчета;
- абсолютная скорость точки в движении относительно неподвижной системы отсчета;
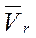 - относительная скорость точки, скорость движения относительно подвижной системы отсчета;
- относительная скорость точки, скорость движения относительно подвижной системы отсчета;
 - переносная скорость точки, скорость той точки подвижной системы отсчета, с которой в данный момент времени совпадает движущаяся точка.
- переносная скорость точки, скорость той точки подвижной системы отсчета, с которой в данный момент времени совпадает движущаяся точка.
Если переносным движением является вращательное движение (рис. 108), переносной скоростью  для точки будет являться скорость точки вращающегося конуса (подвижной системы отсчета), где в данный момент времени находится движущаяся точка М.
для точки будет являться скорость точки вращающегося конуса (подвижной системы отсчета), где в данный момент времени находится движущаяся точка М.
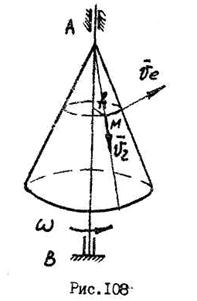
Численное значение скорости  зависит от угловой скорости вращающегося тела и расстояния
зависит от угловой скорости вращающегося тела и расстояния  точки до оси вращения. Расстояние
точки до оси вращения. Расстояние  зависит от относительного движения точки вдоль образующей конуса. Модуль абсолютной скорости определяется по правилу параллелограмм:
зависит от относительного движения точки вдоль образующей конуса. Модуль абсолютной скорости определяется по правилу параллелограмм: 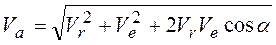 , (2.41)
, (2.41)
где 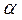 - угол между направляющими векторов
- угол между направляющими векторов 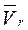 и
и  . Если векторы
. Если векторы 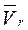 и
и  взаимно перпендикулярны (рис. 108), то
взаимно перпендикулярны (рис. 108), то
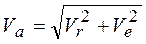 . (2.42)
. (2.42)
Если векторы 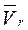 и
и  лежат в одной плоскости (рис. 109), то модуль абсолютной скорости удобно определить по проекциям на координатные оси
лежат в одной плоскости (рис. 109), то модуль абсолютной скорости удобно определить по проекциям на координатные оси

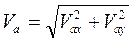 ,
,
где 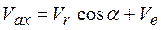 ,
,  .
.
Абсолютное ускорение точки равно геометрической сумме трех ускорений:
· относительного  , характеризующего изменение относительной скорости точки в относительном движении;
, характеризующего изменение относительной скорости точки в относительном движении;
· переносного 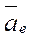 , характеризующего изменение переносной скорости точки в переносном движении;
, характеризующего изменение переносной скорости точки в переносном движении;
· ускорения Кориолиса 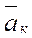 , характеризующего изменение относительной скорости точки в переносном движении и переносной скорости точки в относительном движении:
, характеризующего изменение относительной скорости точки в переносном движении и переносной скорости точки в относительном движении:
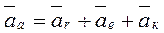 . (2.43)
. (2.43)
Относительное и переносное ускорение определяется из закона соответствующего движения. Ускорение Кориолиса вычисляется по формуле:
 , (2.44)
, (2.44)
где 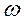 - угловая скорость переносного вращательного движения.
- угловая скорость переносного вращательного движения.
Модуль ускорения Кориолиса зависит от угла между векторами 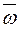 и
и 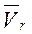 :
:
 . (2.45)
. (2.45)
Ускорение Кориолиса равно нулю, если а) 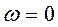 , т.е. переносное движение не является вращательным; б) векторы
, т.е. переносное движение не является вращательным; б) векторы 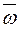 и
и 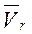 параллельны между собой, т.е.
параллельны между собой, т.е.
 .
.
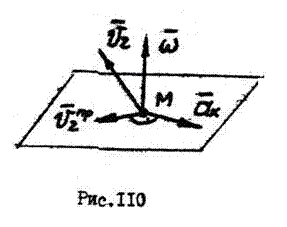
Чтобы определить направление вектора ускорения Кориолиса по правилу Жуковского необходимо:
1. перенести в точку М вектор угловой скорости переносного вращательного движения;
2. спроецировать вектор относительной скорости 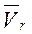 на плоскость, перпендикулярную вектору
на плоскость, перпендикулярную вектору 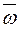 ;
;
3. повернуть проекцию 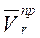 на
на 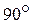 в сторону вращения (рис. 110).
в сторону вращения (рис. 110).
Если переносное движение поступательное, то  ,
,  , поэтому абсолютное ускорение будет равно геометрической сумме относительного и переносного ускорений (рис. 111):
, поэтому абсолютное ускорение будет равно геометрической сумме относительного и переносного ускорений (рис. 111):
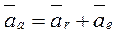 . (2.46)
. (2.46)

При решении задач на сложное движение точки рекомендуется придерживаться следующего порядка:
1. Выяснить, какое движение точки является абсолютным, какое относительным и какое переносным.
2. Используя закон относительного движения, определить положение точки в заданный момент времени.
3. Вычислить относительную и переносную скорости точки, показать векторы переносной и относительной скорости. Вычислить абсолютную скорость точки по правилу параллелограмма или по проекциям на координатные оси.
4. Вычислить составляющие относительного и переносного ускорения и показать на схеме их векторы.
5. В случае переносного вращательного движения определить модуль и направление ускорения Кориолиса.
6. Вычислить модуль абсолютного ускорения точки по проекциям на координатные оси.
ПРИМЕНЕНИЕ ТЕОРЕМЫ О СЛОЖЕНИИ СКОРОСТЕЙ.
Пример №20.
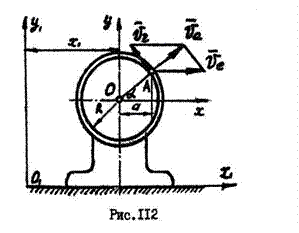
Электромотор (рис. 112), установленный на горизонтальном фундаменте без креплений, движется поступательно и прямолинейно по закону:
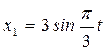 .
.
Ротор мотора вращается вокруг оси  согласно уравнению
согласно уравнению 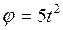 . Определить абсолютную скорость точки ротора, отстоящей от оси вращения ротора на расстоянии
. Определить абсолютную скорость точки ротора, отстоящей от оси вращения ротора на расстоянии  в момент времени
в момент времени  . Положение точки М определяется углом
. Положение точки М определяется углом  .
.
 Решение:
Решение:
1. Точка  совершает абсолютное движение относительно неподвижной системы отсчета
совершает абсолютное движение относительно неподвижной системы отсчета 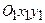 . Подвижная система отсчета
. Подвижная система отсчета  жестко связана с электромотором. Абсолютное движение точки состоит из относительного движения по окружности радиуса R со скоростью
жестко связана с электромотором. Абсолютное движение точки состоит из относительного движения по окружности радиуса R со скоростью 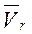 и переносного прямолинейного движения вдоль горизонтального фундамента со скоростью
и переносного прямолинейного движения вдоль горизонтального фундамента со скоростью  .
.
2. Положение точки в заданный момент времени определено углом  .
.
3. Относительную и переносную скорость точки найдем, используя заданные законы относительного и переносного движения. В относительном движении скорость точки М зависит от угловой скорости вращения ротора и расстояния точки до оси вращения:  ,
,
где 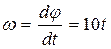 ;
;
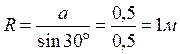 .
.
Следовательно, в заданный момент времени:
 .
.
Переносную скорость точки найдем, дифференцируя по времени уравнение движения электромотора:
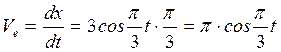 ;
;
при t1=1c 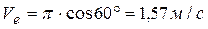 .
.
Абсолютную скорость точки М можно найти по правилу параллелограмма:
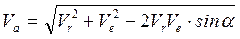 .
.
Учитывая, что  .
.
Абсолютную скорость точки можно найти по проекциям на координатные оси.
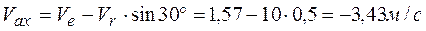 ;
; 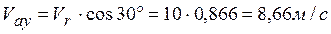 ;
; 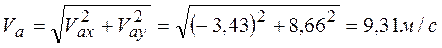 .
.
Пример №21.
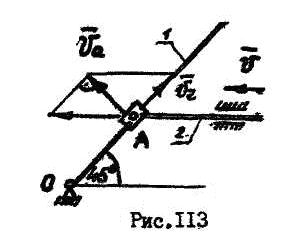
Стержень 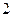 кулисного механизма (рис. 113) движется со скоростью
кулисного механизма (рис. 113) движется со скоростью 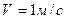 . Для заданного положения механизма определить угловую скорость кулисы
. Для заданного положения механизма определить угловую скорость кулисы 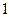 , если расстояние
, если расстояние 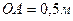 .
.
Решение:
Точка 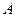 участвует в относительном движении вдоль кулисы
участвует в относительном движении вдоль кулисы 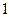 со скоростью
со скоростью 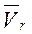 и в переносном движении со стержнем
и в переносном движении со стержнем 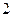 со скоростью
со скоростью  . В абсолютном движении точка
. В абсолютном движении точка 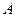 движется по окружности радиуса
движется по окружности радиуса  со скоростью
со скоростью  . Зная переносную скорость
. Зная переносную скорость  , можно найти абсолютную скорость движения точки
, можно найти абсолютную скорость движения точки 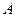 :
: 
 .
.
Учитывая, что 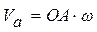 , где
, где  - угловая скорость кривошипа,
- угловая скорость кривошипа,  .
.
ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЯЫ ДЛЯ СЛУЧАЯ ПЕРЕНОСНОГО ПОСТУПАТЕЛЬНОГО УСКОРЕНИЯ.
Пример №22.
Колеса тепловоза одинакового радиуса 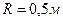 катятся без скольжения по прямолинейному участку пути. Спарник
катятся без скольжения по прямолинейному участку пути. Спарник  соединяющий кривошипы
соединяющий кривошипы  и
и 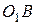 , движется поступательно. Определить абсолютную скорость и абсолютное ускорение точки
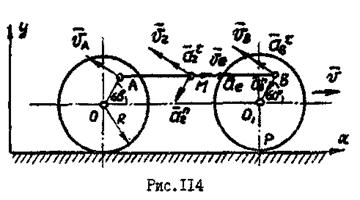
, движется поступательно. Определить абсолютную скорость и абсолютное ускорение точки  спарника тот момент, когда угол поворота кривошипов
спарника тот момент, когда угол поворота кривошипов  и
и 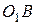 , равен
, равен  и
и 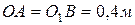 (рис.114), а тепловоз движется с постоянной скоростью
(рис.114), а тепловоз движется с постоянной скоростью 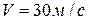 .
.
Решение:
1. Спарник  , на котором находится точка
, на котором находится точка  , движется поступательно, следовательно, все точки спарника движутся по одинаковым траекториям - окружностям радиуса
, движется поступательно, следовательно, все точки спарника движутся по одинаковым траекториям - окружностям радиуса  и имеют равные скорости и ускорения.
и имеют равные скорости и ускорения.
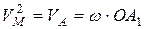
где  - угловая скорость колеса.
- угловая скорость колеса.
Угловую скорость колеса определим, принимая во внимание, что колесо совершает плоскопараллельное движение, центр колеса движется со скоростью 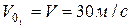 , а мгновенный центр скоростей колеса находится в точке
, а мгновенный центр скоростей колеса находится в точке  :
:
 .
.
Тогда
 .
.
Абсолютную скорость точки  найдем по проекциям на координатные оси:
найдем по проекциям на координатные оси:
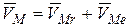 ;
;
 ;
;
где 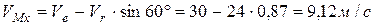 ;
;
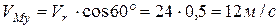 ;
;
 .
.
2. Так как переносное движение является поступательным, абсолютное ускорение точки  определим по формуле:
определим по формуле:
 , (2)
, (2)
где 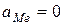 ,
, 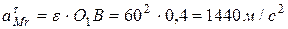 .
.
ПРИМЕНЕНИЕ ТЕОРЕМЫ КОРИОЛИСА.
Пример №23.
Диск радиуса 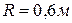 , закрепленный шарнирно в точке
, закрепленный шарнирно в точке 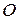 (рис.115), вращается вокруг неподвижной оси с угловой скоростью
(рис.115), вращается вокруг неподвижной оси с угловой скоростью 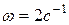 . По ободу диска движется точка
. По ободу диска движется точка  согласно закону относительного движения
согласно закону относительного движения 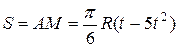 , (
, ( - в сантиметрах,
- в сантиметрах, 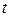 - в секундах). Найти абсолютную скорость и абсолютное ускорение точки
- в секундах). Найти абсолютную скорость и абсолютное ускорение точки  в момент времени
в момент времени  .
.
Решение:
 1. Сложное движение точки
1. Сложное движение точки  складывается из относительного движения по ободу диска по закону
складывается из относительного движения по ободу диска по закону  и переносного вращательного движения с диском относительно оси
и переносного вращательного движения с диском относительно оси 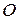 .
.
2. Положение точки в заданный момент времени определяется дуговой координатой  :
: 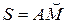 .
.
Дата публикования: 2014-10-20; Прочитано: 642 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
