 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Несобственный интеграл первого рода
|
|
Пусть функция  определена на промежутке
определена на промежутке 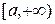 и интегрируема на любом конечном промежутке
и интегрируема на любом конечном промежутке 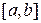 ,
, 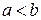 .
.
Определение. Несобственным интегралом от функции  по промежутку
по промежутку 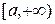 называют
называют 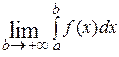 и обозначают
и обозначают 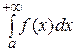 . Если указанный выше предел существует, то говорят, что несобственный интеграл сходится и справедливо равенство
. Если указанный выше предел существует, то говорят, что несобственный интеграл сходится и справедливо равенство 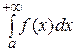 =
= 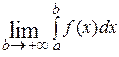 . Если же указанный предел не существует или равен бесконечности, тогда говорят, что несобственный интеграл расходится.
. Если же указанный предел не существует или равен бесконечности, тогда говорят, что несобственный интеграл расходится.
Если  непрерывна на промежутке
непрерывна на промежутке 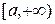 , тогда у неё существует первообразная
, тогда у неё существует первообразная 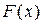 а этом промежутке и из определения несобственного интеграла вытекает практический способ вычисления этого интеграла
а этом промежутке и из определения несобственного интеграла вытекает практический способ вычисления этого интеграла 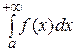 =
= 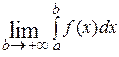 =
= 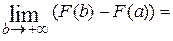
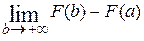 = =
= = 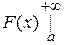 , где подстановка на
, где подстановка на 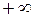 означает что необходимо вычислить
означает что необходимо вычислить 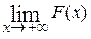 . Из сказанного выше следует, что в несобственном интеграле первого рода можно делать замену переменной и интегрировать по частям также, как и в определённом интеграле.
. Из сказанного выше следует, что в несобственном интеграле первого рода можно делать замену переменной и интегрировать по частям также, как и в определённом интеграле.
Пример. Вычислим 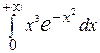 . Произведём в данном интеграле замену переменной
. Произведём в данном интеграле замену переменной 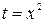 . Тогда
. Тогда 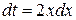 ,
, 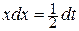 , а
, а 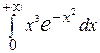 = =
= = 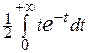 = (интегрируем по частям
= (интегрируем по частям 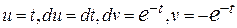 ) =
) =
= 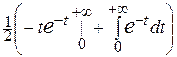 =
= 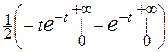 =
= 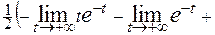
+ 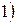 =
= 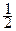 . Так как
. Так как 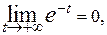
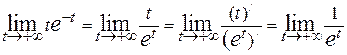 = = 0.
= = 0.
Следовательно, данный несобственный интеграл сходится и равен 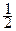 .
.
Аналогичным образом определяется несобственный интеграл от функции  по промежутку
по промежутку 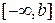 , а именно
, а именно 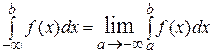 .
.
Пример. Вычислим 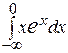 . Интегрируя по частям
. Интегрируя по частям 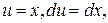
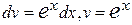 , получим
, получим 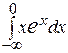 =
= 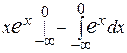 =
= 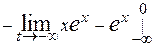 = =
= = 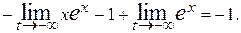 Так как
Так как 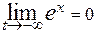 ,
,  . Следовательно, рассматриваемый интеграл сходится и равен –1.
. Следовательно, рассматриваемый интеграл сходится и равен –1.
Если функция  определена на промежутке
определена на промежутке 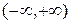 и интегрируема на любом конечном промежутке
и интегрируема на любом конечном промежутке 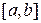 , тогда несобственный интеграл
, тогда несобственный интеграл  .
.
Пример. Вычислим 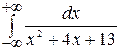 . Выделив полный квадрат, полу-
. Выделив полный квадрат, полу-
чим 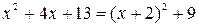 , а интеграл
, а интеграл 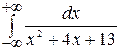 =
= 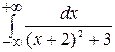 = =
= = 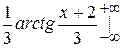 =
= 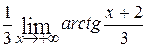 –
– 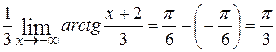 .
.
Дата публикования: 2014-10-20; Прочитано: 292 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
