 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Экстремум функции двух переменных
|
|
Определение. Точка 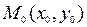 называется точкой локального максимума (локального минимума) функции
называется точкой локального максимума (локального минимума) функции 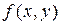 , если существует число
, если существует число
∆ > 0 такое, что для любых точек плоскости 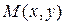 , удовлетворяющих неравенству
, удовлетворяющих неравенству 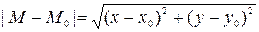 < ∆, выполняется неравенство
< ∆, выполняется неравенство 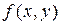 ≤
≤ 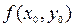 (
(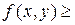
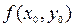 для точки локального минимума).
для точки локального минимума).
Необходимый признак экстремума. Если точка 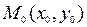 является точкой локального экстремума (точкой локального максимума или минимума) функции
является точкой локального экстремума (точкой локального максимума или минимума) функции 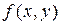 и в этой точке существуют частные производные первого порядка
и в этой точке существуют частные производные первого порядка 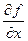 ,
, 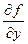 , тогда
, тогда 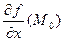 =
= 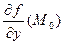 = 0.
= 0.
Точки плоскости, в которых частные производные первого порядка равны нулю, называют стационарными точками функции 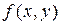 . Из необходимого признака экстремума следует, что для отыскания точек локального экстремума функции необходимо сначала найти стационарные точки этой функции.
. Из необходимого признака экстремума следует, что для отыскания точек локального экстремума функции необходимо сначала найти стационарные точки этой функции.
Например, стационарные точки функции 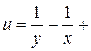
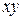 являются решением системы двух уравнений с двумя неизвестными
являются решением системы двух уравнений с двумя неизвестными 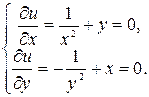
Из первого уравнения системы получаем 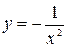 . Подставив это выражение во второе уравнение вместо y, получим равенство
. Подставив это выражение во второе уравнение вместо y, получим равенство 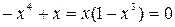 , из которого находим два корня
, из которого находим два корня 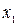 = 0,
= 0, 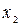 = 1. Первый корень не входит в область определения функции, а по второму корню
= 1. Первый корень не входит в область определения функции, а по второму корню 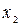 = 1 находим
= 1 находим 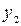 = –1 и стационарную точку
= –1 и стационарную точку 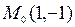 .
.
Достаточный признак экстремума. Пусть точка 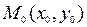 является стационарной точкой функция
является стационарной точкой функция 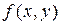 (
(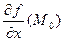 =
= 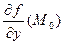 = 0), и функция имеет в этой точке непрерывные частные производные до второго порядка включительно. Обозначим A =
= 0), и функция имеет в этой точке непрерывные частные производные до второго порядка включительно. Обозначим A = 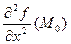 , B =
, B = 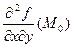 , C =
, C = 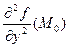 , ∆ = AC ─ B
, ∆ = AC ─ B 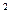 . Тогда: 1) если A > 0 и ∆ > 0, то
. Тогда: 1) если A > 0 и ∆ > 0, то 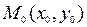 является точкой локального минимума; 2) если A < 0 и ∆ > 0, то
является точкой локального минимума; 2) если A < 0 и ∆ > 0, то 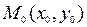 является точкой локального максимума; 3) если ∆ < 0, то
является точкой локального максимума; 3) если ∆ < 0, то 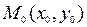 не является точкой локального экстремума; 4) если A = 0 либо ∆ = 0, тогда требуется дополнительное исследование.
не является точкой локального экстремума; 4) если A = 0 либо ∆ = 0, тогда требуется дополнительное исследование.
Пример. Найдём точки локального экстремума функции 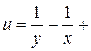 +
+ 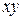 . Ранее была найдена единственная стационарная точка этой функции
. Ранее была найдена единственная стационарная точка этой функции 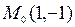 . Вычисляем частные производные второго порядка в стационарной точке. Имеем,
. Вычисляем частные производные второго порядка в стационарной точке. Имеем, 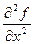 =
= 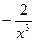 ,
, 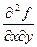 = 1,
= 1, 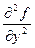 =
= 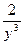 . Следовательно, A = =
. Следовательно, A = = 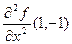 = ─2, B = 1, C =
= ─2, B = 1, C = 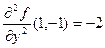 , ∆ = AC – B
, ∆ = AC – B 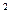 = 4 – 1 = 3 > 0.
= 4 – 1 = 3 > 0.
Таким образом, A = – 2 < 0, ∆ = 3 > > 0 и точка 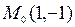 является точкой локального максимума рассматриваемой функции.
является точкой локального максимума рассматриваемой функции.
Пусть поверхность в пространстве задана уравнением 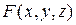 = 0 и точка
= 0 и точка 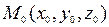 принадлежит этой поверхности, то есть
принадлежит этой поверхности, то есть 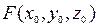 = =0. Тогда уравнение касательной плоскости, проведенной к этой поверхности в точке
= =0. Тогда уравнение касательной плоскости, проведенной к этой поверхности в точке 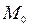 , имеет вид
, имеет вид
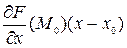 +
+ 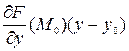 +
+ 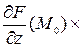
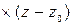 = 0.
= 0.
В частности, когда уравнение поверхности задано уравнением z = = 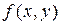 , это уравнение можно переписать в виде
, это уравнение можно переписать в виде 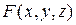 =
= 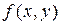 – z = =0. Тогда будет
– z = =0. Тогда будет 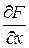 =
= 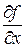 ,
, 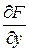 =
= 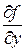 ,
, 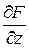 = –1, а уравнение касательной плоскости примет следующий вид
= –1, а уравнение касательной плоскости примет следующий вид
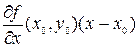 +
+ 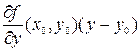 –
– 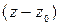 = 0, где
= 0, где 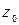 =
= 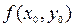 .
.
Составим уравнение касательной плоскости к поверхности, заданной уравнением 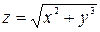 в точке (–1,2). Находим, что
в точке (–1,2). Находим, что 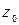 =
= 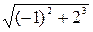 = 3. В нашем случае
= 3. В нашем случае 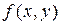 =
= 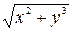 , следовательно,
, следовательно, 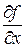 =
= 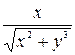 ,
, 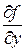 = =
= = 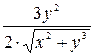 . Таким образом,
. Таким образом, 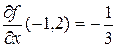 ,
, 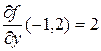 и уравнение искомой касательной плоскости имеет вид
и уравнение искомой касательной плоскости имеет вид 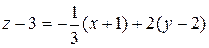 . Умножив последнее равенство на 3, и перенося всё в левую часть, получим окончательно
. Умножив последнее равенство на 3, и перенося всё в левую часть, получим окончательно 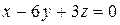 .
.
Задание 6. Определение. Функция 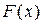 называется первообразной для функции
называется первообразной для функции  на промежутке
на промежутке 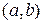 , если для любых
, если для любых 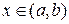 выполняется равенство
выполняется равенство 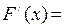
 .
.
Свойства первообразной. 1). Если 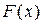 – первообразная для функции
– первообразная для функции  , тогда
, тогда 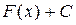 , где
, где 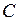 – произвольная постоянная, тоже является первообразной для
– произвольная постоянная, тоже является первообразной для  . 2). Если
. 2). Если 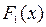 ,
, 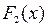 – первообразные для функции
– первообразные для функции  , тогда
, тогда 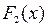 =
= 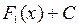 , где
, где 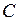 – постоянная, 3). Если
– постоянная, 3). Если 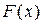 – первообразная для функции
– первообразная для функции  , тогда
, тогда 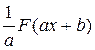 – первообразная для функции
– первообразная для функции 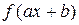 . Например,
. Например, 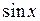 – первообразная для функции
– первообразная для функции 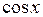 (так как
(так как 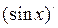 =
= 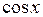 ), следовательно, функция
), следовательно, функция 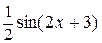 будет первообразной для функции
будет первообразной для функции 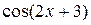 .
.
Неопределённый интеграл. Из свойств первообразной следует, что множество всех первообразных для функции  можно представить в виде
можно представить в виде 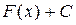 , где
, где 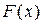 – одна из первообразных, C – произвольная постоянная.
– одна из первообразных, C – произвольная постоянная.
Определение. Неопределённым интегралом от функции  назы-
назы-
вается множество всех первообразных для этой функции; неопределённый
интеграл обозначают 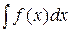 . Следовательно,
. Следовательно, 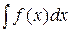 =
= 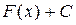 , где
, где
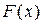 – одна из первообразных. Например,
– одна из первообразных. Например, 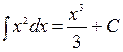 .
.
Свойства неопределённого интеграла. 1). Линейность 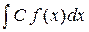 = =
= = 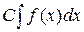 (постоянный множитель можно вынести за знак интеграла);
(постоянный множитель можно вынести за знак интеграла); 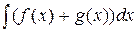 =
= 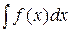 +
+ 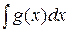 (интеграл от суммы функций равен сумме интегралов). Например,
(интеграл от суммы функций равен сумме интегралов). Например, 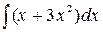 =
= 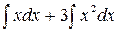 2) =
2) = 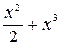 + +C. 2)
+ +C. 2) 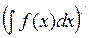 =
=  (производная от неопределённого интеграла равна подинтегральной функции). 3)
(производная от неопределённого интеграла равна подинтегральной функции). 3) 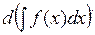 =
= 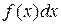 (дифференциал от неопределённого интеграла равен подинтегральному выражению).
(дифференциал от неопределённого интеграла равен подинтегральному выражению).
Таблица неопределённых интегралов
1. 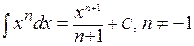 ;
;
2. 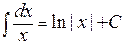 ;
;
3. 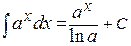 , в частности
, в частности 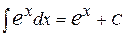 ;
;
4. 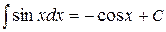 ;
;
5. 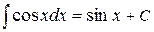 ;
;
6. 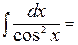
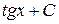 ;
;
7. 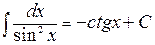 ;
;
8. 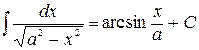 , в частности
, в частности 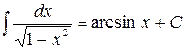 ;
;
9. 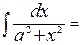
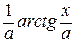
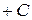 , в частности
, в частности 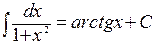 ;
;
10. 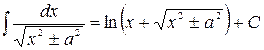 .
.
Докажем равенство 10. По определению первообразной нужно доказать, что производная правой части этого равенства равна подинтегральной функции. Действительно, имеем 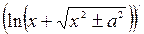 =
= 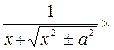
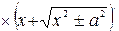 =
= 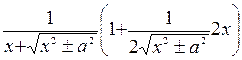 =
= 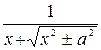
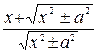 = =
= = 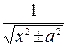 .
.
Пример. Вычислим 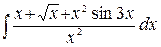 . Поделив числитель подинтегральной дроби на знаменатель, а затем, применив свойство линейности неопределённого интеграла, получаем равенства
. Поделив числитель подинтегральной дроби на знаменатель, а затем, применив свойство линейности неопределённого интеграла, получаем равенства 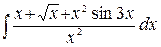 = =
= = 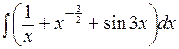 =
= 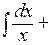
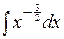 +
+ 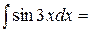
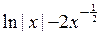 –
– 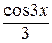
+ 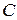 =
= 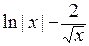 –
– 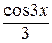 +
+ 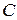 .
.
Формула интегрирования по частям. Если 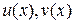 – непрерывно дифференцируемые функции, тогда справедливо равенство
– непрерывно дифференцируемые функции, тогда справедливо равенство
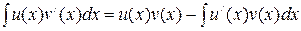 , (11)
, (11)
которое называют формулой интегрирования по частям.
Рассмотрим интегралы, которые вычисляются только с помощью этой формулы.
1. Интегралы вида 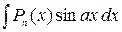 ,
, 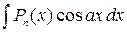 ,
, 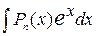 , где
, где 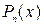 – полином степени
– полином степени 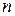 , вычисляются
, вычисляются 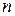 – кратным интегрированием по частям (формула интегрирования по частям применяется столько раз, какова степень полинома). При этом полагают
– кратным интегрированием по частям (формула интегрирования по частям применяется столько раз, какова степень полинома). При этом полагают 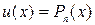 ,
, 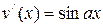 , либо
, либо 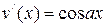 , либо
, либо 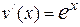 . При каждом интегрировании по частям степень полинома уменьшается на единицу.
. При каждом интегрировании по частям степень полинома уменьшается на единицу.
Пример. Вычислим 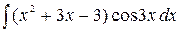 . Воспользовавшись формулой (10), получим
. Воспользовавшись формулой (10), получим 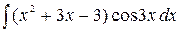 =
= 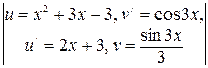 = =
= = 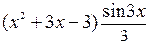 –
– 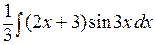 = (применим ещё раз формулу (11)) =
= (применим ещё раз формулу (11)) = 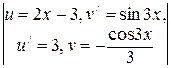 =
= 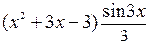 –
– 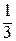
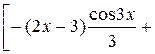
+ 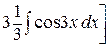 =
= 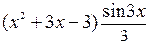 +
+ 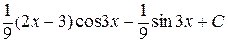 .
.
2. Интегралы вида 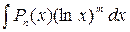 вычисляются
вычисляются 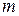 – кратным интегрированием по частям (формула интегрирования по частям применяется столько раз, какова степень логарифма). При этом полагают
– кратным интегрированием по частям (формула интегрирования по частям применяется столько раз, какова степень логарифма). При этом полагают 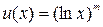 ,
, 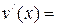
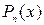 . При каждом интегрировании по частям степень логарифма уменьшается на единицу.
. При каждом интегрировании по частям степень логарифма уменьшается на единицу.
Пример. Вычислим с помощью формулы интегрирования по частям 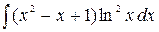 =
= 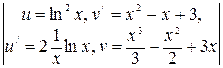 =
= 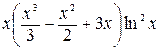 –
–
– 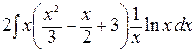 = (применим опять формулу интегрирования по
= (применим опять формулу интегрирования по
частям) = 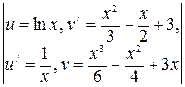 =
= 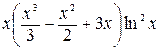 – 2
– 2 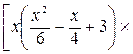
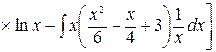 =
= 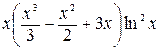 –
– 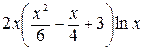 +
+
+ 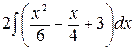 =
= 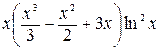 –
– 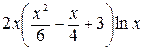 +
+ 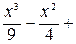 +
+ 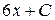 .
.
3. Интегралы, в которых под знаком интеграла находятся обратные тригонометрические функции, тоже вычисляются интегрированием по частям. Это интегралы вида 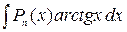 ,
, 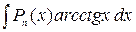 ,
, 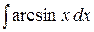 ,
, 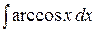 . При вычислении этих интегралов за
. При вычислении этих интегралов за 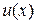 обозначают обратные тригонометрические функции.
обозначают обратные тригонометрические функции.
Пример. Вычислим 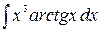 =
= 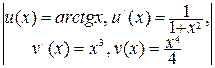 =
= 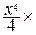
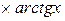 –
– 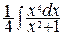 =
= 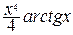 –
– 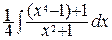 =
= 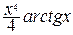 –
– 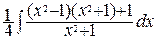 = =
= = 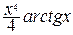 –
– 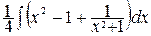 =
= 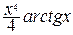 –
– 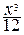 +
+ 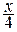 –
– 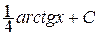 .
.
Замена переменной в неопределённом интеграле. Пусть функция 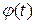 непрерывно дифференцируема, а функция
непрерывно дифференцируема, а функция  непрерывна, тогда справедливо равенство
непрерывна, тогда справедливо равенство 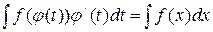 , которое называют формулой замены переменной в неопределённом интеграле.
, которое называют формулой замены переменной в неопределённом интеграле.
Пример. Для вычисления 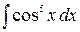 сделаем замену
сделаем замену 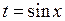 ,
, 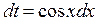 , тогда получим
, тогда получим 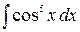 =
= 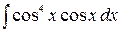 =
= 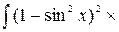
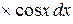 =
= 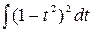 =
= 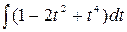 =
= 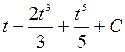 =
= 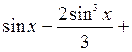
+ 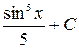 .
.
Пример. Для вычисления 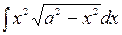 сделаем замену
сделаем замену 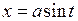 ,
, 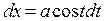 ,
, 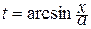 , тогда получим
, тогда получим 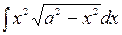 = =
= = 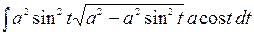 =
= 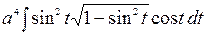 =
= 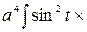
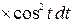 =
= 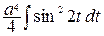 =
= 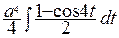 =
= 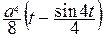 =
= 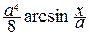 –
– 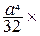
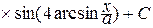 .
.
Задание 7. Пусть функция  определена на промежутке
определена на промежутке 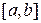 . Точки
. Точки 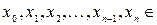
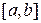 такие, что
такие, что 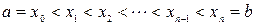 называют разбиением промежутка
называют разбиением промежутка 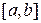 . Число
. Число 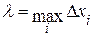 ,
, 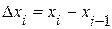 ,
, 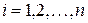 , называют рангом разбиения
, называют рангом разбиения 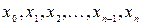 . Выберем произвольным образом
. Выберем произвольным образом 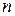 точек
точек 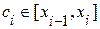 . Сумму
. Сумму 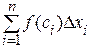 называют интегральной суммой для функции
называют интегральной суммой для функции  на промежутке
на промежутке 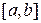 , соответствующей данному разбиению.
, соответствующей данному разбиению.
Определение. Определённым интегралом от функции  по промежутку
по промежутку 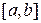 называют предел интегральных сумм, когда ранг разбиения стремится к 0. Определённый интеграл от функции
называют предел интегральных сумм, когда ранг разбиения стремится к 0. Определённый интеграл от функции  по промежутку
по промежутку 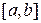 обозначают
обозначают 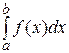 . Следовательно,
. Следовательно, 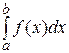 =
= 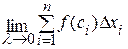 . Если определённый интеграл существует, то говорят, что функция
. Если определённый интеграл существует, то говорят, что функция  интегрируема на промежутке
интегрируема на промежутке 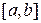 .
.
Дата публикования: 2014-10-20; Прочитано: 741 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
