 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Элементы теории вероятностей
|
|
6.3.1. Функция распределения, условие ее нормировки.
Основой молекулярно-кинетической теории является представление о хаотичном, беспорядочном движении молекул. Вопрос о величине скорости и энергии этого движения был одним из первых, который предстояло решить. Задача была решена Д. Максвеллом в середине прошлого века. Речь шла, естественно, не о скорости и энергии каждой молекулы, но о каких-то средних для системы молекул значениях этих величин. Решить подобную задачу можно, лишь пользуясь основными понятиями теории вероятностей, где рассматриваются законы, характерные для событий, называемых случайными.
Случайное событие может состояться, а может и не состояться, в отличие от закономерного события, которое предопределено законом. Так, скорость тела, движущегося с известным ускорением а,может быть точно рассчитана для любого момента времени по уравнению равноускоренного движения. Скорость же конкретной молекулы непредсказуема, она меняется в зависимости от случайных условий.
Из совокупности случайных величин принято выделять благоприятные события. Например, при стрельбе в мишень результат каждого выстрела можно считать случайным событием. Среди них будет несколько благоприятных, например, попавших в центр мишени. Рассматриваемое понятие субъективно или, скорее, зависит от цели проводимого эксперимента: событие, благоприятное для получения ожидаемого результата в одном опыте, может быть неблагоприятным в другом опыте. Так, рассчитывая эмиссию молекул с поверхности нагретого тела, благоприятным событием мы будем считать встречу молекулы большой скорости. Решая задачу о сжижении газа, мы, наоборот, за благоприятное событие сочтем встречу молекулы, обладающей малой скоростью.
Итак, пусть имеется большое число  однотипных событий (выстрел по мишени, например). Из них
однотипных событий (выстрел по мишени, например). Из них 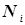 будет благоприятных. Вероятностью благоприятного события назовем отношение
будет благоприятных. Вероятностью благоприятного события назовем отношение
 . .
| (6.22) |
В случае, если Ni = N, то есть все встретившиеся события благоприятны, вероятность wi будет равна единице. Это – максимально возможное значение вероятности. Оно носит название достоверности.
Часто бывает, что значения рассматриваемых случайных величин непрерывны. Например, возраст студентов, находящихся в аудитории, – величина случайная, меняющаяся непрерывно: в аудитории может присутствовать студент в возрасте 18 лет, 6 месяцев и 3 дня; 18 лет, 5 месяцев, 20 дней и т.д. Возраст студентов представит непрерывный ряд значений. В этом случае ставить вопрос о вероятности найти в аудитории студента с возрастом ровно 18 лет не имеет смысла: такого студента, скорей всего, в аудитории не окажется. При постановке вопроса о вероятности нужно указывать не точный возраст, а с каким-либо интервалом: год, месяц, неделя и т.д. Например: 18 лет 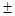 1/2 года; 18 лет
1/2 года; 18 лет 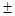 3 месяца.
3 месяца.
В случае непрерывной случайной величины число благоприятных событий нужно заменить интервалом: Ni ® dN. Тогда вероятность встретить значение случайной величины в данном интервале будет частью полной вероятности:
 . .
| (6.23) |
Обозначим случайную величину через x. Тогда интервал  значений случайной величины покажет точность, с которой мы указывали эту случайную величину: х+dx. Точность (то есть ширина интервала), с которой указывается значение случайной величины, выбирается произвольно. Но чем шире интервал (больше dx), тем больше вероятность встретить заданное значение случайной величины. Так, в рассмотренном примере с возрастом студентов, вероятность встретить в аудитории студента, которому 18 лет
значений случайной величины покажет точность, с которой мы указывали эту случайную величину: х+dx. Точность (то есть ширина интервала), с которой указывается значение случайной величины, выбирается произвольно. Но чем шире интервал (больше dx), тем больше вероятность встретить заданное значение случайной величины. Так, в рассмотренном примере с возрастом студентов, вероятность встретить в аудитории студента, которому 18 лет 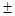 1/2 года больше, чем вероятность встретить студента, которому 18 лет
1/2 года больше, чем вероятность встретить студента, которому 18 лет 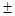 3 дня. Иначе говоря, вероятность dw пропорциональна ширине dx выбранного интервала:
3 дня. Иначе говоря, вероятность dw пропорциональна ширине dx выбранного интервала:
| dw = kdx | (6.24) |

|
В свою очередь, коэффициент k не является постоянной величиной, он зависит от положения интервала dx на оси x (рис. 6.5).
Действительно, несмотря на то, что величина интервалов одинакова, т.е. dx1= dx2= dx3, вероятность встретить студента с возрастом, принадлежащим интервалу dx1, будет существенно отлична от вероятности встретить студента с возрастом в интервале dx2. Уравнение (6.24) следует изменить так, чтобы отметить факт непостоянства коэффициента k, его зависимость от x:
| dw = f(x)dx, | (6.25) |
где f(x) носит название функции распределения.
Равенство (6.25) так же, как и (6.22), служит определением вероятности случайного события. Сравнивая эти два равенства, получим для функции распределения следующее выражение:
f(x) =  . .
| (6.26) |
То есть, функция распределения показывает относительное число благоприятных событий в единичном интервале изменения случайной величины.
Если нужно найти вероятность w для конечного интервала D x = x 2 – x 1 изменения случайной величины, то она выразится интегралом:
w =  . .
| (6.27) |
Отыскивая вероятность по всей области существования случайной величины x, следует брать бесконечные пределы:
w = 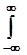 f(x)dx. f(x)dx.
| (6.28) |
В последнем случае вероятность равна достоверности: w = 1, следовательно
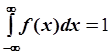 . .
| (6.29) |
Полученное уравнение называют условием нормировки функции распределения. Пределы в (6.29) показывают, что суммирование ведется по всему интервалу возможных значений случайной величины. В зависимости от того, что мы понимаем под x, бесконечность принимает то или иное значение. Так, например, в случае с вычислением среднего возраста студента за  можно принять, скажем, 50 или 60 лет, а за
можно принять, скажем, 50 или 60 лет, а за 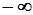 – 5 или 7 лет .
– 5 или 7 лет .
6.3.2. Применение функции распределения.
Функция распределения может быть использована для нахождения средней величины. Рассмотрим пример. Пусть имеется N песчинок. Найдем <x> – средний линейный размер песчинки:
 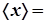 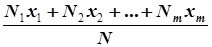 , ,
| (6.30) |
где  – число песчинок размером x 1, N2 – размером x 2 и т.д. Поделив почленно, получим:
– число песчинок размером x 1, N2 – размером x 2 и т.д. Поделив почленно, получим:
 , ,
| (6.31) |
или, заменяя  через dwi, найдем среднее значение:
через dwi, найдем среднее значение:
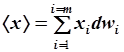 . .
| (6.32) |
Для непрерывной случайной величины dw = f(x)dx и вместо суммирования нужно интегрировать:
 . .
| (6.33) |
Следовательно, для нахождения среднего значения случайной величины нужно знать вид функции распределения f(x), то есть форму ее зависимости от случайной величины x.
Дата публикования: 2014-10-19; Прочитано: 634 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
