Их модули и векторы. Связь с полным ускорением

Помимо полного ускорения, определяемого по (2.6), существуют ещё два ускорения. В этом нетрудно убедиться, заменив вектор скорости 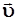произведением:

,

(2.7)

где – единичный вектор, направленный по скорости. Тогда вектор ускорения, как производная от произведения двух функций, предстанет в виде суммы двух векторов:

,

(2.8)

каждый из которых является одной из составляющих вектора ускорения.

Первый из этих векторов назовем тангенциальным ускорением, так как он направлен по касательной к траектории:

.

(2.9)

Очевидно, что тангенциальное ускорение характеризует быстроту изменения модуля скорости (длины вектора 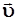). Величина вектора 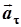, а точнее, его проекция на направление скорости, определяется как производная от модуля скорости по времени:

.

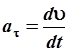(2.10)

Последнее уравнение показывает, что a _t может иметь знак: оно будет отрицательным, если скорость убывает, т.к. в этом случае d u – приращение модуля скорости – отрицательно. Движение с убывающей скоростью называется замедленным. Очевидно, что при замедленном движении вектор тангенциального ускорения направлен противоположно вектору скорости.

Второй вектор в сумме (2.8) называют нормальным ускорением. Этот вектор связан со скоростью изменения направления скорости . Величину и направление вектора нормального ускорения

(2.11)

найдем из следующих соображений.

Прежде всего, из (2.8) следует, что полное ускорение будет равно нормальному в случае равенства нулю тангенциального ускорения. Если к этому добавить определение полного ускорения (2.6), получим:

.

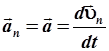(2.12)

Введенный в уравнение индекс n, которого не было ранее, означает, что приращение скорости взято для частного случая, когда тангенциальное ускорение равно нулю, то есть длина вектора скорости не меняется. При этом условии изменится и рис. 2.5, где вектор 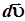направлен под углом к траектории, изменяющимся в зависимости от соотношения длин векторов.

На рис. 2.6а изображены два вектора скорости равной длины. При этом вектор их изменения направлен под углом, близким к прямому. То же самое наблюдается при построении чертежа на рис. 2.6б, где точка движется по окружности радиуса R, не меняя величины своей скорости. Векторы 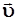изображены в трех точках, а для нахождения приращения вектора скорости начала векторов перенесены в точку A.

Если последовательно изобразить векторы скорости во всех точках окружности, а затем для нахождения векторов их разностей перенести их начала в точку A, получим вторую окружность, составленную векторами .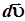

Радиусом окружности будет модуль u вектора скорости. Длина этой новой окружности 2 pu будет суммой модулей отдельных векторов 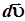за то время, пока точка совершит полный оборот по своему пути 2 p R. Это время будет равно отношению пройденного точкой пути к скорости ее движения:

.

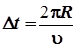(2.13)

Если, следуя (2.12), изменение скорости разделить на то время, за которое оно произошло, получим модуль нормального ускорения:

.

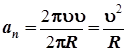(2.14)

Направление же нормального ускорения совпадает с вектором 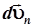, а последний вектор всегда перпендикулярен скорости, так как является элементом окружности, в которой скорость является радиусом (см. рис. 2.6).

Скорость всегда направлена по касательной к траектории, значит нормальное ускорение направлено по радиусу к центру ее кривизны. Поэтому его еще называют центростремительным.

Итак, определив третью кинематическую характеристику движения материальной точки – полное ускорение по (2.6) – мы пришли к выводу, что существуют ещё два вида ускорения – тангенциальное и нормальное, модули которых находятся по (2.10) и (2.14) соответственно. На рис. 2.7 изображены вектора этих ускорений в одной точке криволинейной траектории. Естественно, они перпендикулярны друг другу. Согласно (2.8) их геометрическая сумма должна дать полное ускорение, которое, как и на рис. 2.4, направлено под углом к траектории внутрь ее кривизны:

.

(2.15)

Модуль полного ускорения:

.

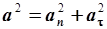(2.16)

Все три ускорения характеризуют неравномерное движение по кривой. При равномерном движении по любой траектории a _t = 0, а при движении по прямой обращается в нуль нормальное ускорение.