Затухающие колебания

В уравнении (4.9) второго закона Ньютона суммой всех сил является возвращающая сила, без которой колебания невозможны. В случае, когда действует сила трения (а она действует практически всегда), следует учесть ещё эту силу. Она, как известно, направлена в сторону, противоположную скорости, и ее величина пропорциональна скорости тела:

,

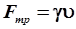(4.17)

где 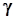– коэффициент сопротивления среды.

С учетом этой силы второй закон Ньютона для тела массой m, колеблющегося вдоль оси ОХ примет вид:

.

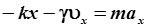(4.18)

Работа сил трения приводит к убыли энергии колеблющегося тела:

.

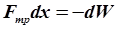(4.19)

Уравнение имеет тот недостаток, что не содержит t, хотя очевидно, что убыль энергии пропорциональна времени. Введём его:

.

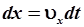(4.20)

Тогда, с учетом (4.17), из выражения (4.19) получим:

.

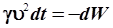(4.21)

Опыт показывает, что затухание – убыль энергии колеблющегося тела – зависит от его массы. Более инертное тело, тело с большей массой труднее останавливается, энергия его убывает медленно. Введя в (4.21) массу, получим:

.

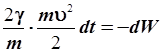(4.22)

Поскольку при колебательном движении полная энергия может быть представлена как две кинетических, то

,

(4.23)

и после интегрирования в пределах от 0 до t и от W_o до W получим:

.

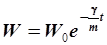(4.24)

Заменив полную энергию по (4.16) через kA²/2,после сокращения и извлечения корня получим выражение для амплитуды затухающих колебаний:

.

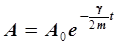(4.25)

Величину 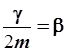называют коэффициентом затухания.

Уравнение (4.25) свидетельствует, что амплитуда колебаний убывает, асимптотически приближаясь к оси времени (рис. 4.5). Отношение двух амплитуд, взятых через период, носит название декремента затухания. Найдем его, записав значения амплитуд:

; .

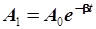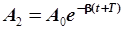(4.26)

В приведенных выше уравнениях индексом ноль помечена амплитуда на момент начала колебаний. Поделив уравнения (4.26) одно на другое, получим:

,

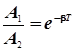(4.27)

и, после логарифмирования:

.

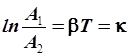(4.28)

В уравнении (4.27) определяется декремент затухания, а в следующем, (4.28) – его логарифм k ("каппа" ). Последний носит название логарифмического декремента. Он связан с периодом через коэффициент затухания и является характеристикой затухающего колебания, оставаясь постоянным в течение всего колебательного процесса.

Подводя итог, заметим, что уравнение затухающих колебаний записывается в привычном для нас виде периодической функции смещения x от времени, но амплитуда колебаний уменьшается с течением времени по полученному выше закону (4.25):