Собственная частота

Основной закон динамики остается таковым и для колебательного движения. Его запись, правда, имеет некоторые особенности: ускорение при колебаниях всегда направлено в сторону положения равновесия. Значит, как этого требует второй закон Ньютона, к положению равновесия, противоположно смещению, будет направлена и сумма всех сил системы. Для начала заменим ускорение в правой части второго закона по (4.6):

.

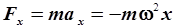(4.7)

Произведение массы колеблющегося тела на квадрат частоты колебаний можно обозначить через k, так как обе величины постоянны:

.

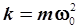(4.8)

Введенный выше коэффициент k носит название коэффициента жёсткости системы. Он определяет частоту колебаний и зависит от конструкции самой колеблющейся системы. Уравнение свидетельствует, что период колебаний для данной системы постоянен, а частота колебаний носит название собственной частоты. Она, как и период, определяется параметрами колеблющейся системы и не зависит от каких либо внешних факторов. Чтобы подчеркнуть этот момент, частоте, входящей в уравнение (4.8), присвоен индекс "0". Ниже будут рассмотрены случаи, вынуждающие систему колебаться с иной частотой. Но, будучи предоставленной самой себе, система всегда колеблется с частотой 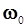, которая не зависит от того, какова амплитуда этих колебаний. Убедитесь в этом сами: колеблющееся тело может иметь как малую, так и большую амплитуду колебаний. При большой амплитуде тело движется с большой скоростью (см. формулу (4.6)). При малой – скорость его невелика, так как за то же время, определяемое периодом, тело проходит меньшее расстояние.

Воспользовавшись понятием коэффициента жёсткости, можно изменить вид уравнения (4.7):

.

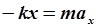(4.9)

Левая часть уравнения имеет размерность силы и по своей зависимости от x похожа на упругую силу. Это, как правило, не одна сила, а сумма всех сил, действующих на колеблющееся тело.. Её часто называют квазиупругой силой, либовозвращающей силой. Выражение (4.9) есть второй закон Ньютона для колебаний. Он даёт возможность вычислить период колебаний любой колеблющейся системы.

Рассмотрим в качестве примера математический маятник (рис. 4.4). Нетрудно показать силы, действующие на него. Их будет две – сила тяжести и сила натяжения нити. Движение колеблющегося тела – переменное, и ускорение направлено к положению равновесия. Значит, туда же будет направлена и сумма этих двух сил. При достаточно длинной нити и малом смещении из положения равновесия отношение катета к гипотенузе будет равно отношению возвращающей силы F к силе тяжести :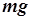

,

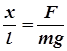(4.10)

или

.

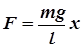(4.11)

Возвращающая сила оказывается пропорциональной смещению x. Используя коэффициент этой пропорциональности в законе Ньютона (4.9), получим:

,

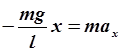(4.12)

или, подставив вместо ускорения его значение:

,

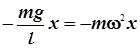(4.13)

получаем: w ² = g / l, что приводит к известной формуле Гюйгенса для периода колебаний математического маятника:

.

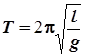(4.14)

В теории колебаний принято считать второй закон Ньютона (4.9) динамическим уравнением свободных гармонических колебаний (дифференциальное уравнение второго порядка), а функцию x (t) (4.2) – его решением. Действительно, подставив смещение x и его вторую производную в (4.9), получим тождество при введённом выражением (4.8) коэффициенте k.