 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Елементів фільтрів
|
|
| n | Фільтр Баттерворта | Фільтр Бесселя | Фільтр Чебишева (0,5 дБ) | Фільтр Чебишева (2 дБ) | |||
| К | 
| К | 
| К | 
| К | |
| 1,586 1,152 2,235 1,068 1,586 2,483 1,038 1,337 1,889 2,610 | 1,274 1,432 1,606 1,607 1,692 1,908 1,781 1,835 1,956 2,192 | 1,268 1,084 1,759 1,040 1,364 2,023 1,024 1,213 1,593 2,184 | 1,231 0,597 1,031 0,396 0,768 1,011 0,297 0,599 0,861 1,006 | 1,842 1,582 2,660 1,537 2,448 2,846 1,522 2,379 2,711 2,913 | 0,907 0,471 0,964 0,316 0,730 0,983 0,238 0,572 0,842 0,990 | 2,114 1,924 2,782 1,891 2,648 2,904 1,879 2.605 2,821 2,946 |
Дещо складніше побудувати фільтр Бесселя і Чебишева. Як і в попередньому випадку з’єднується необхідна кількість секцій 2–х полюсних фільтрів з вказаним для кожної секції коефіцієнтом підсилення (див.
табл. 13.1). В кожній секції попередньо забезпечується рівність  і
і  . Але далі для кожної секції необхідно забезпечити свій добуток RC, який обчислюється за допомогою множників нормування
. Але далі для кожної секції необхідно забезпечити свій добуток RC, який обчислюється за допомогою множників нормування  (див. табл. 13.1) за виразом
(див. табл. 13.1) за виразом  . Для фільтра Чебишева
. Для фільтра Чебишева 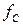 – частота, на якій АЧХ падає нижче діапазону нерівномірності при переході до смуги затримки. У випадку збільшення нерівномірності АЧХ в смузі для фільтрів Чебишева вдається отримати більшу крутість АЧХ в перехідній області.
– частота, на якій АЧХ падає нижче діапазону нерівномірності при переході до смуги затримки. У випадку збільшення нерівномірності АЧХ в смузі для фільтрів Чебишева вдається отримати більшу крутість АЧХ в перехідній області.
Для побудови фільтрів ВЧ використовуються дзеркальні до схеми фільтрів НЧ схеми, тобто схеми де R i C поміняні місцями. При цьому для фільтра Баттерворта значення  і
і  лишаються без змін. Для фільтрів Бесселя і Чебишева значення
лишаються без змін. Для фільтрів Бесселя і Чебишева значення 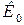 лишаються без змін, а нормуючий множник
лишаються без змін, а нормуючий множник  змінюється на зворотній, тобто
змінюється на зворотній, тобто 
Смуговий фільтр отримується при каскадному з’єднанні фільтрів ВЧ і НЧ з перетинальними смугами пропускання. Смугозатримувальний фільтр можна отримати при паралельному з’єднанні фільтрів НЧ і ВЧ зі смугами, що не перетинаються. Смуга пропускання смугового фільтра визначається як ширина характеристики між точками –3дБ, окрім, рівнохвильових фільтрів, для яких ця ширина визначається точками, де характеристика спадає на величину пульсації у смузі пропускання. Але такі фільтри не можуть застосовуватись у випадках коли необхідні фільтри з високою добротністю. У таких випадках слід застосовувати однокаскадну смугову схему або фільтри, що будуються на основі методу змінного стану. Навіть однокаскадний двополюсний фільтр може мати АЧХ з гострим викидом.
13.7 Фільтри, що будуються на основі методу змінного стану
Ідею синтезу на основі уявлення про змінний стан можна реалізувати на прикладі реалізації ланки другого порядку. Нехай
 (13.7)
(13.7)
або

Переходячи від зображення до оригіналу і враховуючи, що множення на р у часовій області відповідає операції диференціювання, находимо

Звідки

У якості змінних вибираємо 

 i
i  Схеми структурна і електрична, що відповідає останньому рівнянню зображені на
Схеми структурна і електрична, що відповідає останньому рівнянню зображені на
рис. 13.8 (а, б).
У якості основного елемента фільтра вибрані ОП, які за допомогою зовнішніх елементів (R, C) легко перетворюються у інтегратор і суматор.

Рисунок 13.8 – Функціональні схеми ФНЧ – 2–го порядку, який побудований за методом змінного стану: а) спрощена; б) електрична
Зразок смугового фільтра, побудованого на основі методу змінного стану, наведено на рис. 13.9. Цей фільтр набагато складніший у порівнянні з фільтрами на ДНКН, але такі фільтри широко застосовуються завдяки підвищеній стійкості і легкості регулювання.
Не дивлячись на велику кількість елементів, фільтр, що побудований на основі методу змінного стану, є найбільш вдалою схемою для реалізації високодобротних смугових фільтрів. Він відзначається малою поелементною чутливістю, не висуває вимог до смуги пропускання ОП, а також зручний у настроюванні. Наприклад, в схемі, що наведена на рис. 13.9, і використовується у якості смугопроникального. За допомогою двох резисторів  встановлюється центральна частота смуги пропускання
встановлюється центральна частота смуги пропускання  , у той час як резистори
, у той час як резистори  i
i  cпільно визначають добротність Q і коефіцієнт підсилення в смузі пропускання
cпільно визначають добротність Q і коефіцієнт підсилення в смузі пропускання 



 |
Рисунок 13.9 – Функціональна схема фільтру на основі методу змінного стану
Цей фільтр може бути зроблений таким, що перестроюється з фіксованою добротністю, при використанні у якості резистора  двосекційного змінного резистора. З другого боку, змінним можна зробити резистор
двосекційного змінного резистора. З другого боку, змінним можна зробити резистор  , при цьому отримаємо фільтр з фіксованою частотою і змінною добротністю (і на жаль зі змінним коефіцієнтом підсилення).
, при цьому отримаємо фільтр з фіксованою частотою і змінною добротністю (і на жаль зі змінним коефіцієнтом підсилення).
 |
Найбільш близькі до фільтрів на основі методу змінного стану так звані біквадратні фільтри, рис. 13.10.
Рисунок 13.10 – Функціональна схема біквадратного фільтру
Особливістю такого фільтра є можливість регулювання його частоти (за допомогою  ) при зберіганні сталості ширини смуги пропускання. Розрахункові рівняння
) при зберіганні сталості ширини смуги пропускання. Розрахункові рівняння

Сама добротність Q визначається як  і дорівнює
і дорівнює  При зміні значення центральної частоти
При зміні значення центральної частоти  пропорційно змінюється і добротність Q при цьому зберігається незмінною.
пропорційно змінюється і добротність Q при цьому зберігається незмінною.
У випадку проектування біквадратного фільтра необхідно виконати таку послідовність дій:
1. Вибрати ОП з шириною смуги, яка у 10 – 20 разів перевищує добуток 
2. Підібрати заокруглений номінал конденсатора, ближчий до такого значення 
3. Використати перше наведене вище рівняння для розрахунку опору  і відповідно друге для обчислення за заданим значенням ширини смуги
і відповідно друге для обчислення за заданим значенням ширини смуги  номінала опору
номінала опору  .
.
4. Згідно з третім рівнянням отримати значення опору 
Слід відзначити, що кожний з опорів  ,
,  i
i  є навантаженням для ОП, і тому їх номінали не повинні бути менші за 5 кОм.
є навантаженням для ОП, і тому їх номінали не повинні бути менші за 5 кОм.
Припустимо, що необхідно розрахувати смуговий фільтр з параметрами 

 Задамося
Задамося  потім визначимо
потім визначимо  (
( ) і
) і  (
(
 ) і зрештою
) і зрештою  (
( ).
).
Якщо розрахункові значення резисторів виходять дуже великі або малі, то необхідно підібрати інший номінал конденсатора.
Для отримання смугових фільтрів високого порядку необхідно зробити каскадне з’єднання кількох фільтрів низького порядку, комбінуючи їх таким чином, щоб забезпечити характеристику фільтра, що вимагається. У такому випадку, як і раніше, фільтр Баттерворта має «максимально плоску» АЧХ, у той час як фільтр Чебишева задовольняє вимоги крутого зламу АЧХ в перехідній області. Збільшення крутості АЧХ шляхом підключення додаткових секцій призводить, як правило, до погіршення перехідної і фазової характеристик.
13.8 Схемні рішення фільтрів
Подвійний Т–подібний фільтр
Відомі подвійні Т–подібні фільтри, що випускаються у вигляді готових модулів для діапазону частот від 1 Гц до 50 кГц з глибиною послаблення на частоті провалу близько 60 дБ. Такі фільтри використовують пасивний подвійний Т–подібний фільтр, рис. 13.11, який має нескінченне придушення на частоті  . Такий фільтр діє так ефективно тому, що має місце підсумовування двох сигналів, які на частоті зрізу мають різницю фаз 1800. Отримання необхідної характеристики вимагає доброго узгодження елементів. Для отримання глибокого і стабільного провалу АЧХ слід вибирати конденсатори і резистори зі стабільними параметрами і малою температурною залежністю. Збільшення крутості провалу відбуваєть
. Такий фільтр діє так ефективно тому, що має місце підсумовування двох сигналів, які на частоті зрізу мають різницю фаз 1800. Отримання необхідної характеристики вимагає доброго узгодження елементів. Для отримання глибокого і стабільного провалу АЧХ слід вибирати конденсатори і резистори зі стабільними параметрами і малою температурною залежністю. Збільшення крутості провалу відбуваєть
 |
ся при збільшенні підсилення у колі зворотного зв’язку, рис. 13.12.
Рисунок 13.11 – Електрична схема пасивного подвійного Т–подібного фільтру

Рисунок 13.12 – Функціональна схема Т–подібного фільтру зі стежним зв’язком
Фільтри на основі принципу інверсії імпедансу
Схема смугового фільтра, що реалізує принцип інверсії імпедансу наведена на рис. 13.13.
Величина еквівалентної індуктивності визначається за виразом

Резонансна частота фільтра дорівнює
 .
.
 |
Рисунок 13.13 – Схема електрична принципова смугового фільтра, що реалізує принцип інверсії імпедансу
Опір шунтувального резистора  , що визначає еквівалентний резонансний опір контуру, дорівнює
, що визначає еквівалентний резонансний опір контуру, дорівнює

Застосування гіраторів дозволяє значно спростити конструкцію деяких пристроїв, наприклад, еквалайзерів. На низьких частотах такі пристрої вимагають дуже великого значення індуктивності. Так, для частоти  при ємності контуру
при ємності контуру  величина еквівалентної індуктивності дорівнює
величина еквівалентної індуктивності дорівнює  Гіраторна схема малочутлива до відхилення параметрів елементів, що її утворюють.
Гіраторна схема малочутлива до відхилення параметрів елементів, що її утворюють.
Фільтри на основі конденсаторів комутування
Відомий спосіб побудови інтеграторів, які складають основу біквадратних фільтрів і фільтрів на основі методу змінного стану. Основна його ідея полягає у використанні аналогових МДН–ключів, що синхронізуються зовнішнім сигналом прямокутної форми і високої частоти, як правило, у 100 разів вищої, ніж у аналогових сигналів, що обробляються. На рис.13.14 (а, б) наведено схеми інтеграторів на конденсаторах комутування.
При увімкненні ключа S1 має місце заряд конденсатора С1 до напруги  , тобто він зберігає заряд
, тобто він зберігає заряд  у другій половині робочого циклу конденсатор С1 розряджається через віртуальну землю, передаючи свій заряд конденсатору С2. Сама напруга на конденсаторі С2 змінюється, відповідно, на величину
у другій половині робочого циклу конденсатор С1 розряджається через віртуальну землю, передаючи свій заряд конденсатору С2. Сама напруга на конденсаторі С2 змінюється, відповідно, на величину  Слід відзначити, що вихідна напруга змінюється протягом кожного циклу ВЧ прямокутного коливання пропорційно напрузі
Слід відзначити, що вихідна напруга змінюється протягом кожного циклу ВЧ прямокутного коливання пропорційно напрузі  (зміна якого за один період керуючого коливання передбачається дуже незначною), тобто ця схема є інтегратором напруги вхідного сигналу
(зміна якого за один період керуючого коливання передбачається дуже незначною), тобто ця схема є інтегратором напруги вхідного сигналу
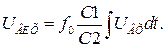

Рисунок 13.14 – Функціональні схеми інтеграторів на конденсаторах комутування:
а – на перемикних конденсаторах; б – звичайний інтегратор
Застосування конденсаторів комутування, замість звичайних інтеграторів дає такі переваги. Перше, такий фільтр дозволяє застосовувати більш дешеві конденсатори, оскільки коефіцієнт передачі такого інтегратора залежить тільки від співвідношення конденсаторів С1 і С2, а не від їх значень, у той час як отримання резисторів і конденсаторів з точним значенням і високою стабільністю є досить складним. Друге полягає у можливості перестроювання частоти фільтра зміною частоти керуючого коливання, оскільки характеристична частота біквадратного фільтра, чи йому подібного, залежить тільки від коефіцієнта передачі інтегратора.
Мають такі фільтри і деякі недоліки. Перше, це наскрізне проходження сигналу тактової (керуючої) частоти, але звичайно це не має значення, оскільки цей сигнал значно віддалений від смуги, яку займає сигнал, що обробляється. Друга проблема, якщо у вхідному сигналі присутні спектральні компоненти, що знаходяться поблизу тактової частоти, то вони будуть накладатися на смугу пропускання. Для усунення цього явища у вхідному сигналі не повинно бути означених складових. Це може бути забезпечено застосуванням звичайного RC–фільтра. І третє – це зниження динамічного діапазону сигналу за рахунок зростання рівня шуму.
Фазові коректори (ланки)
Фазові ланки – це пристрої, де на заданій частоті фаза вихідного сигналу отримує зсув відносно вхідного на визначене значення, при цьому модуль коефіцієнта передачі не змінюється у всьому робочому діапазоні частот.
Як показано вище, коефіцієнт передачі фазової ланки першого порядку має вигляд

де 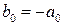 ,
, 
Модуль коефіцієнта передачі

Фаза вихідного сигналу

де 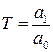 – стала часу фазозадавального кола.
– стала часу фазозадавального кола.
З різних варіантів фазових ланок першого порядку слід відзначити схеми фазовипереджувальних і фазозапізнювальних ланок, рис. 13.15 (а,б).

Рисунок 10.15 – Фазові ланки
Рисунок 13.15 – Функціональні схеми фазових коректорів (ланок) першого порядку:
а – фазовипереджувальна ланка; б – фазозапізнювальна ланка
Фазовий зсув в цих ланках визначається виразом

Знак перед виразом визначає фазовипереджувальну чи фазозапізнювальну ланки.
Запитання та завдання для самоконтролю
1. На який параметр АЧХ впливає порядок активного фільтра?
2. Які шляхи наближення АЧХ активного фільтра до ідеальної?
3. Які властивості має активний фільтр Баттерворта (Чебишева, Бесселя)?
4. Наведіть рівняння коефіцієнту передачі а) ФВЧ, б) ФНЧ, в) смугопроникального фільтра, в) смугозатримувального фільтра та г) фазового коректора. Поясніть вплив його коефіцієнтів.
5. Зобразіть графіки нормованих АЧХ фільтрів а) Беттверворта, б) Бесселя та в) Чебишева різних порядків. Поясніть по цим графікам вплив величини порядку фільтра на його вибірні властивості.
6. Які основні схемотехнічні засоби реалізації активних фільтрів?
7. Cпроектуйте ФНЧ (ФВЧ) Чебишева п’ятого порядку з нерівномірністю АЧХ в смузі пропускання 1 дБ і частотою зрізу 100 Гц. Ємності конденсаторів не повинні перевищувати 0,1 мкФ.
8. Розрахувати параметри схеми активного ФНЧ другого порядку на основі ОП, якщо частота зрізу  , а коефіцієнт передачі фільтра К = 2,75.
, а коефіцієнт передачі фільтра К = 2,75.
9. Розрахувати параметри схеми активного ФВЧ другого порядку на основі ОП, якщо частота зрізу  , а коефіцієнт передачі фільтра К = 1,65.
, а коефіцієнт передачі фільтра К = 1,65.
10. Що таке фазові коректори?
11. Поясніть методику проектування фільтрів на основі методу змінного стану. Що таке біквадратні фільтри?
12. Які підходи до проектування фільтрів на основі конденсаторів комутування?
Література [27-35]
Дата публикования: 2014-11-18; Прочитано: 1716 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
