 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Розрахунок каскадів на ОП
|
|
Нехай необхідно побудувати підсилювач на основі неінвертувального включення ОП, з вхідним опором 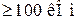 ,
, 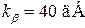 , смуга частот
, смуга частот 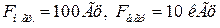 . Коефіцієнти частотних спотворень на цих частотах не повинні перевищувати 3 дБ. Операційний підсилювач має внутрішню корекцію, його параметри:
. Коефіцієнти частотних спотворень на цих частотах не повинні перевищувати 3 дБ. Операційний підсилювач має внутрішню корекцію, його параметри: 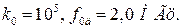 Живлення однополярне.
Живлення однополярне.
Спочатку обираємо схему (рис. 12.22).
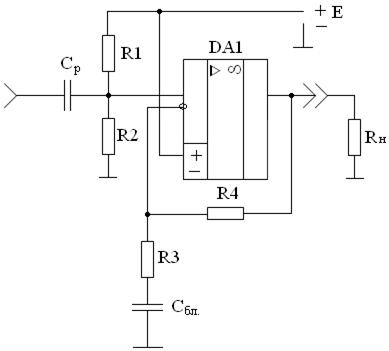
Рисунок 12.22 – Принципова схема неінвертуючого підсилювача
Для забезпечення 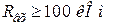 обираємо
обираємо 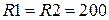 кОм.
кОм.
В такому випадку
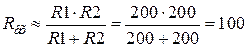 кОм.
кОм.
Для забезпечення 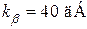 (100раз) з умови
(100раз) з умови
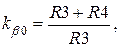
обираємо 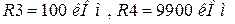 .
.
Визначаємо 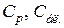
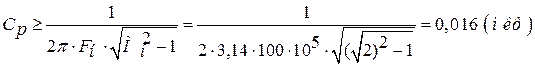 .
.
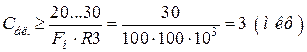 .
.
Перевіримо виконання коефіцієнта частотних спотворень 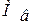 для частоти
для частоти 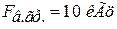
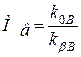 ,
,
де 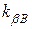 - фактичний коефіцієнт підсилення підсилювача на частоті
- фактичний коефіцієнт підсилення підсилювача на частоті 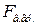
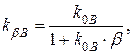
де 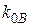 - коефіцієнт підсилення ОП з розімкненим колом ВЗЗ на частоті
- коефіцієнт підсилення ОП з розімкненим колом ВЗЗ на частоті 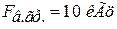 ;
; 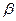 - коефіцієнт передачі кола ВЗЗ.
- коефіцієнт передачі кола ВЗЗ.
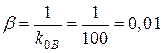 .
.
Оскільки ОП має внутрішню корекцію, його АЧХ з розімкненим колом ВЗЗ має вигляд (рис. 12.23):
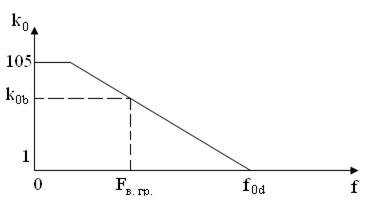
Рисунок 12.23 – АЧХ обраного ОП
З рисунка 12.23, можна визначити 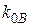 для части
для части 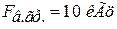 . Для нахилу АЧХ -20дб/дек,
. Для нахилу АЧХ -20дб/дек,
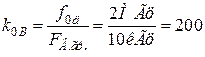 .
.
Визначимо 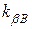
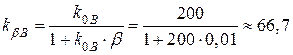 .
.
Коефіцієнт частотних спотворень дорівнює
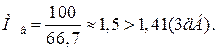
У такий спосіб задача не розв’язана.
Проектований підсилювач треба будувати, як послідовне з’єдння двох каскадів, з 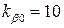 тобто
тобто
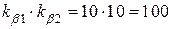 .
.
В цьому випадку номінали елементів будуть дорівнювати 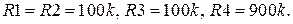
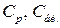 без змін.
без змін.
Коефіцієнт передачі кола ЗЗ складає
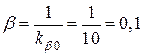 ,
,
тоді
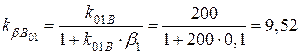 .
.
Результуючий коефіцієнт підсилення двох каскадів складає
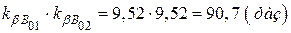 .
.
Коефіцієнт частотних спотворень відповідно
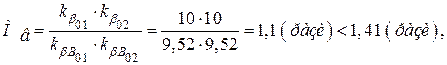
тобто рівень частоти спотворень задовольняє вимогам.
Остаточна принципова схема підсилювача подана нижче
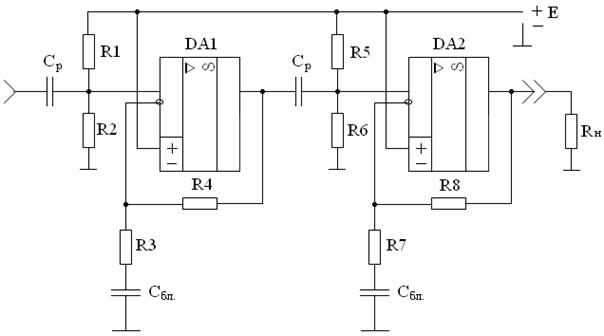
Рисунок 12.24 – Принципова схема розрахованого підсилювача
12.9 Запитання та завдання для самоконтролю
1. Побудувати схему двокаскадного диференціального підсилювача на основі ОП. Забезпечити загальний коефіцієнт підсилення 100. Передбачити можливість балансування нуля схеми.
2. Спроектуйте інвертувальний підсилювач на ОП з коефіцієнтом підсилення 50, забезпечте його смугу пропускання 100 Гц – 50 кГц, вхідний опір не менше 100 кОм. Живлення однополярне. Тип ОП – К140УД12.
3. Визначить смугу пропускання неінвертувального підсилювача, якщо він виконаний на ОП К140УД7 і забезпечує коефіцієнт підсилення 20, значення розділового конденсатора 1,0 мкФ, вхідний опір 100 кОм.
4. Яким вимогам повинен відповідати ОП інвертора імпедансу?
5. Які коефіцієнти підсилення каскадів К1 та К2 помножувача ємності?
6. Які опори (вхідний, вихідний) повинні бути забезпечені в помножувачі ємності?
7. Визначити 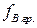 (Мн = Мв = 3 дБ) повторювача напруги на ОП, якщо операційний підсилювач має внутрішню корекцію, а його параметри:
(Мн = Мв = 3 дБ) повторювача напруги на ОП, якщо операційний підсилювач має внутрішню корекцію, а його параметри: 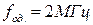 ;
; 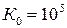 . Інші параметри ОП відповідають ідеальному ОП.
. Інші параметри ОП відповідають ідеальному ОП.
8. Побудувати підсилювач на основі неінвертувального включення ОП (живлення двополярне) з вхідним опором 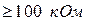 ,
, 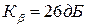 для смуги частот
для смуги частот 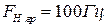 ,
, 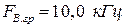 за умови Мн = Мв = 3 дБ. Операційний підсилювач має внутрішню корекцію, його параметри
за умови Мн = Мв = 3 дБ. Операційний підсилювач має внутрішню корекцію, його параметри 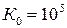 ,
, 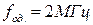 .
.
Література [27-35]
13 Активні фільтри
13.1 Загальні відомості про фільтри
При використанні ОП як одного з елементів пристрою з’являється можливість синтезувати характеристику будь–якого LC фільтра без використання котушок індуктивності. Такі фільтри відомі під назвою «активних фільтрів», у зв’язку з наявністю в схемі активного елемента (ОП).
Активні фільтри можна використовувати для реалізації фільтрів НЧ,ВЧ, смугопроникальних і смугозатримувальних, вибираючи тип фільтра у залежності від його властивостей; рівномірності підсилення в смузі пропускання, крутості перехідної ділянки АЧХ або незалежності часу затримки від частоти. Окрім цього можна також побудувати «усепроникаючі фільтри» з плоскою АЧХ, але нестандартною ФЧХ (такі фільтри називають «фазові коректори»), або навпаки фільтри з постійним фазовим зсувом, але довільною АЧХ.
Коефіцієнт передачі фільтра у загальному випадку можна записати у вигляді
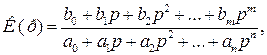 (13.1)
(13.1)
де 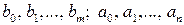 – дійсні числа; р – оператор Лапласа, для синусоїдального сигналу
– дійсні числа; р – оператор Лапласа, для синусоїдального сигналу 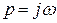 .
.
Порядок фільтра визначається найбільшим степенем оператора р у знаменнику. Якщо відомі корені 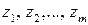 чисельника і корені
чисельника і корені 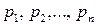 знаменника, то коефіцієнт передачі можна записати у вигляді
знаменника, то коефіцієнт передачі можна записати у вигляді
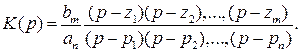 (13.2)
(13.2)
При 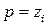 коефіцієнт передачі дорівнює нулю, тому корені
коефіцієнт передачі дорівнює нулю, тому корені 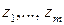 називають нулями. При
називають нулями. При 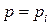 коефіцієнт передачі дорівнює нескінченності, тому корені
коефіцієнт передачі дорівнює нескінченності, тому корені 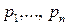 називають полюсами.
називають полюсами.
Коефіцієнт передачі фільтра повністю визначається значеннями нулів і полюсів, а також сталим множником 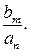
Коефіцієнт передачі фільтра першого порядку
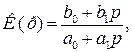 (13.3)
(13.3)
де 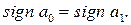
У відповідності з виразом (13.3) коефіцієнт передачі фільтра НЧ може бути записаний при 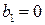
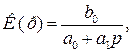
- для ФВЧ, при 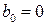
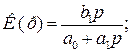
- для фазового коректора, при 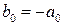 ,
, 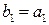
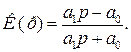
Коефіцієнт передачі фільтра другого порядку
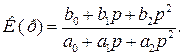 (13.4)
(13.4)
Виходячи з виразу (13.4), коефіцієнт передачі відповідних фільтрів можна подати у вигляді:
- для ФНЧ, при 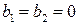
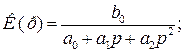
- для ФВЧ, при 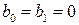
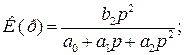
- для смугопроникального фільтра, при 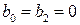
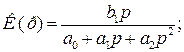
- для смугозатримувальних фільтрів, при 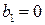
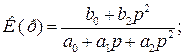
- для фазового коректора, при 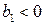
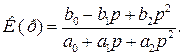
Фільтри другого порядку можна реалізувати, з’єднуючи відповідним чином ланки першого і нульового порядку. Спосіб такої реалізації витікає з можливої форми подання коефіцієнта передачі у вигляді елементарних функцій інтегрування, диференціювання, підсумовування. Оскільки способів подання виразу (13.4) через елементарні функції може бути досить багато, то і число можливих схемних рішень фільтрів другого порядку може бути значним.
На практиці фільтр характеризується трьома основними параметрами: 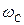 – характеристична частота (зрізу), що характеризує рівень послаблення АЧХ –3 дБ;
– характеристична частота (зрізу), що характеризує рівень послаблення АЧХ –3 дБ; 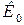 модуль коефіцієнта передачі у смузі пропускання;
модуль коефіцієнта передачі у смузі пропускання; 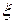 – коефіцієнт згасання коливань.
– коефіцієнт згасання коливань.
Смуга пропускання і добротність Q пов’язані з коефіцієнтом згасання співвідношенням
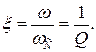
Відомі три найбільш популярні типи активних фільтрів: Баттерворта, (максимально плоска характеристика в смузі пропускання), фільтр Чебишева (найбільш крутий перехід від смуги пропускання до смуги придушення) та фільтр Бесселя (максимально плоска характеристика часу затримки). Будь–який з цих фільтрів можна реалізувати за допомогою різних схем. Всі вони придатні для побудови фільтрів верхніх, нижніх частот і смугових фільтрів.
13.2 Фільтри Баттерворта і Чебишева
Фільтр Баттерворта, як відзначено вище, забезпечує найбільш плоску характеристику в смузі пропускання, що однак досягається за рахунок повільної зміни характеристики у перехідній області, тобто між смугами пропускання і затримки. Він також має погану фазочастотну характеристику, тобто таку, що викликає значні фазові спотворення. Його амплітудно–частотна характеристика задається таким виразом
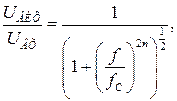 (13.5)
(13.5)
де n – визначає порядок фільтра (число полюсів); 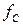 – частота зрізу.
– частота зрізу.
Збільшення числа полюсів дає можливість зробити більш плоскою ділянку АЧХ в смузі пропускання і збільшити крутість спаду від смуги пропускання до смуги затримки, рис. 13.1.
Тобто слід розуміти, що вибираючи фільтр Баттерворта, для досягнення максимально плоскої АЧХ слід поступитися всіма іншими вимогами.
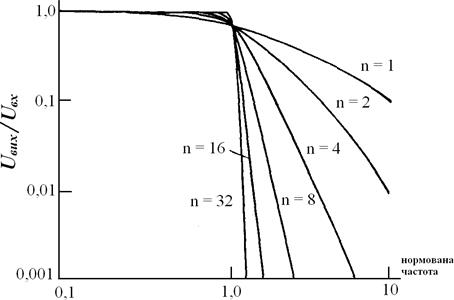
Рисунок 13.1 – Нормовані характеристики фільтра нижніх частот Баттерворта
У більшості випадків найбільш важливим є забезпечення вимоги необхідної нерівномірності в смузі пропускання, яка не повинна перевищувати встановленого значення, наприклад 1 дБ. Фільтр Чебишева відповідає цій вимозі, при цьому допускається деяка нерівномірність по всій смузі, але при цьому значно збільшується крутість зламу АЧХ. Для фільтра Чебишева задаються числом полюсів і нерівномірністю в смузі пропускання. Припускаючи збільшення нерівномірності в смузі, отримають більш крутий злам АЧХ. АЧХ фільтра Чебишева задається таким виразом
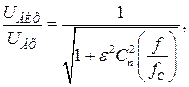 (13.6)
(13.6)
де 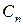 – поліном Чебишева степеня n;
– поліном Чебишева степеня n; 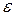 – константа, що визначає нерівномірність АЧХ в смузі пропускання.
– константа, що визначає нерівномірність АЧХ в смузі пропускання.
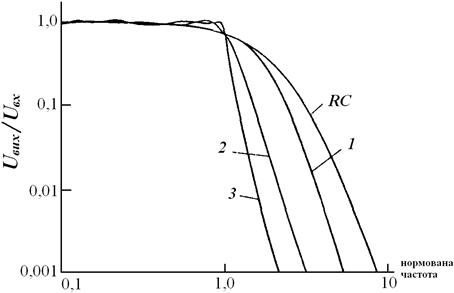
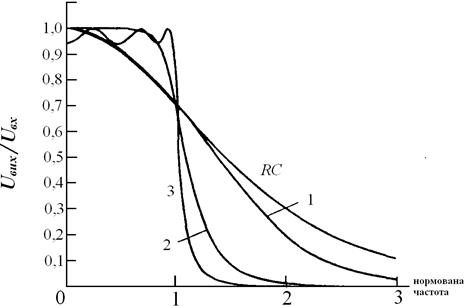
Фільтр Чебишева як і фільтр Баттерворта має ФЧХ, що викликає значні фазові спотворення сигналів. На рис. 13.2(а,б) подані для порівняння характеристики АЧХ 6–полюсних фільтрів нижніх частот, 1 – фільтр Бесселя, 2 – фільтр Баттерворта, 3 – фільтр Чебишева, RC – фільтр. Як можна бачити з рис. 13.2 всі вказані типи фільтрів набагато кращі за RC фільтр.
а)
б)
Рисунок 13.2 – Порівняння характеристики 6–полюсних фільтрів нижніх частот
Але слід відзначити, що і ці типи фільтрів не вільні від недоліків, для фільтра Баттерворта це поступове зниження характеристики при наближенні до частоти 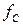 , а для фільтра Чебишева – пульсації, що розподілені по всій смузі, кількість яких зростає разом з порядком фільтра. Окрім цього, активні фільтри, що побудовані з елементів, номінали яких мають деякий допуск, будуть мати характеристики, що відрізняються від розрахункових. На рис. 13.3 проілюстровано цей вплив.
, а для фільтра Чебишева – пульсації, що розподілені по всій смузі, кількість яких зростає разом з порядком фільтра. Окрім цього, активні фільтри, що побудовані з елементів, номінали яких мають деякий допуск, будуть мати характеристики, що відрізняються від розрахункових. На рис. 13.3 проілюстровано цей вплив.
Але разом з вказаними недоліками, фільтр Чебишева є досить раціональною структурою, інколи його називають рівнохвилевим фільтром, оскільки його АЧХ в перехідній області має велику крутість за рахунок того, що в смузі пропускання розподілено декілька рівновеликих пульсацій. Навіть при відносно малих пульсаціях (приблизно 0,1 дБ) фільтр Чебишева забезпечує набагато більшу крутість АЧХ в перехідній області, ніж фільтр Баттерворта. Розрахунок показує, що для забезпечення нерівномірності АЧХ в смузі пропускання не більше 0,1 дБ і згасання 20 дБ на частоті, що відрізняється на 25% від граничної частоти смуги, необхідним є 19–полюсний фільтр Баттерворта і тільки 8–полюсний фільтр Чебишева. Ще кращі показники можуть бути досягнуті у так званих еліптичних фільтрах (або фільтрах Кауера). В таких фільтрах допускаються пульсації АЧХ як в смузі пропускання, так і в смузі затримки для досягнення великої крутості перехідної ділянки АЧХ навіть більшої, ніж у фільтрів Чебишева.
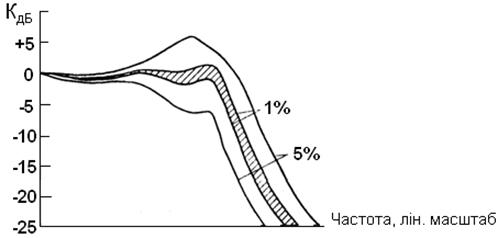
Рисунок 13.3 – Вплив зміни параметрів елементів на характеристику активного фільтра
13.3 Фільтри Бесселя
Як було встановлено раніше, АЧХ фільтра не дає про нього повної інформації. Фільтр навіть з плоскою АЧХ може давати великі фазові спотворення. У тих випадках, коли необхідно зберегти форму сигналу, бажано мати фільтр з лінійною ФЧХ. Вимоги забезпечення лінійної ФЧХ еквівалентні вимогам забезпечення постійного часу затримки. Фільтр Бесселя (друга назва фільтр Томсона) має плоску ділянку частотної характеристики групового часу затримки в смузі пропускання, подібно до того як фільтр Баттерворта має найбільш плоску АЧХ. На рис. 13.4 зображені нормовані за частотою графіки ГЧЗ для 6–полюсних фільтрів нижніх частот Бесселя і Баттерворта.
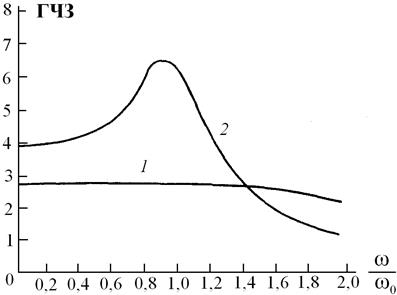
Рисунок 13.4 – Порівняння ГЧЗ для 6–полюсних ФНЧ Бесселя (1) і Баттерворта (2)
Вказана форма характеристики ГЧЗ фільтра Баттерворта викликає появу ефектів викидів при проходженні через фільтр імпульсних сигналів. З другого боку, сталість характеристики ГЧЗ у фільтра Бесселя призводить до ще більш пологої перехідної ділянки, навіть ніж у характеристики фільтра Баттерворта.
Існують способи проектування фільтрів, в яких робиться спроба покращити робочі параметри фільтра Бесселя у частотній області, навіть нехтуючи сталістю ГЧЗ заради зменшення часу зростання і покращення АЧХ. Фільтр Гауса має практично аналогічну до фільтра Бесселя ФЧХ, але кращу перехідну характеристику.
Другий цікавий клас – це фільтри, що дозволяють отримати однакові пульсації кривої часу запізнення у смузі пропускання (аналогічно пульсаціям АЧХ фільтра Чебишева) і забезпечити приблизно однакове запізнення для сигналів зі спектром до смуги затримки. Ще один підхід до створення фільтрів з постійним часом запізнення – це застосування усепроникальних фільтрів, так званих коректорів у часовій області. Такі фільтри мають постійну АЧХ, а зсув фаз може змінюватися відповідно до конкретних вимог. Таким чином, їх можна застосовувати для вирівнювання часу запізнення будь–яких інших фільтрів (Баттерворта або Чебишева).
13.4 Порівняння фільтрів різних типів
Не звертаючи увагу на раніше зроблені зауваження про перехідну характеристику фільтрів Бесселя, слід все ж відзначити, що він має дуже добрі властивості у часовій області у порівнянні з фільтрами Баттерворта і Чебишева. Фільтр Чебишева при його дуже добрій АЧХ має найгірші параметри у часовій області. Фільтр Баттерворта дає компроміс між частотними і часовими характеристиками. На рис. 13.5 подана інформація про робочі характеристики усіх трьох типів фільтрів у часовій області, що доповнює наведені раніше графіки АЧХ. Їх аналіз показує, що у тих випадках, коли важливими є параметри фільтра у часовій області, бажаним є застосування фільтра Бесселя.
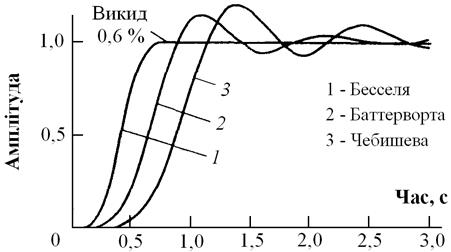
Рисунок 13.5 – Порівняння перехідних процесів для 6–полюсних фільтрів НЧ
13.5 Схеми активних фільтрів на ОП
Відомо багато схем активних фільтрів, які використовуються для отримання необхідної характеристики фільтра, але всі вони повинні відповідати таким вимогам:
– мати малу кількість елементів, як активних, так і пасивних;
– забезпечувати легкість регулювання;
– забезпечувати малий вплив розкиду параметрів елементів, особливо конденсаторів;
– забезпечувати відсутність жорстких вимог до операційного підсилювача, особливо по вимогах швидкості зростання, ширини смуги і вихідному опору;
– забезпечувати можливість створення високодобротних фільтрів;
– забезпечувати нечутливість характеристик фільтрів до коефіцієнта підсилення ОП.
Фільтр, який вимагає використання високоточних елементів, важко наладнати, і по мірі старіння елементів настроювання губиться. Так звана схема фільтра на основі джерела напруги, що керується напругою ДНКН дуже поширена, в основному завдяки своїй простоті і малій кількості елементів, але ця схема є дуже чутливою до зміни параметрів елементів. Для порівняння, зацікавленість, що виникла до складних гіраторних схем, зумовлена їх нечутливістю до малих змін параметрів елементів.
Дата публикования: 2014-11-18; Прочитано: 1628 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
