Каскади з індуктивною ВЧ корекцією

Каскад з індуктивною корекцією показано на рис. 8.6, а.

Корекція здійснюється за допомогою L, що включається послідовно з навантаженням. Така корекція зветься двополюсною або паралельною ВЧ корекцією. Розширення смуги частот у цьому випадку пояснюється тим, що коригуюча індуктивність L, навантаження 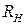та повна ємність каскаду 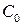утворюють резонансний контур. На низьких та середніх частотах навантаження транзистора практично дорівнює 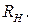На ВЧ при відповідному виборі резонансної частоти 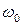та резонансного опору 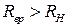можна дістати підсилення тоді як у звичайних каскадах на цих частотах воно вже суттєво менше за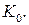

Рисунок 8.6 – Паралельно-індуктивна корекція

Індуктивність L впливає на властивості каскаду тільки в області верхніх частот, тому розрахункові формули для області НЧ та СЧ лишаються без змін. Еквівалентна схема каскаду для верхніх частот показана на
рис. 8.6, б. Щоб здобути широку смугу, опір навантаження транзистора вибирається невеликим. Це дозволяє не враховувати в еквівалентній схемі великі опори 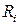та 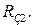При цьому підсилення каскаду на середніх частотах

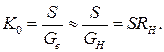
На ВЧ навантаження каскаду являє собою резонансний контур, що має провідність

Підсилення на ВЧ відповідно становить

Для спрощення запису позначимо: 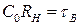– стала часу некоректованого каскаду; 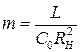– коефіцієнт корекції, що дорівнює квадрату добротності резонансного контуру.

Тоді

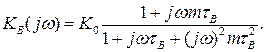
Комплексна частотна характеристика каскаду

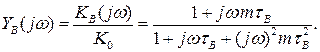
Модуль її дає АЧХ каскаду

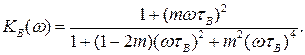(8.8)

Аргумент визначає ФЧХ

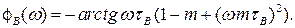(8.9)

У випадку, коли 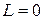та 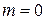вирази (8.8) та (8.9) визначають АЧХ та ФЧХ звичайного резисторного каскаду.

Знайдемо коефіцієнт корекції, що забезпечить найбільше розширення смуги без підйому частотної характеристики (оптимальна частотна характеристика).

Згідно з Брауде запишемо 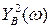у вигляді відношення двох поліномів зі зростаючими ступенями частоти

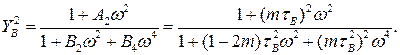
Для корекції необхідно забезпечити 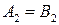або 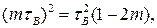звідки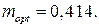

У випадку, коли 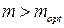на АЧХ виникає підйом, що зростає зі зростанням m. Одночасно з цим має місце незначне зростання смуги частот. На рис. 8.7 побудовані АЧХ каскаду для деяких значень m.

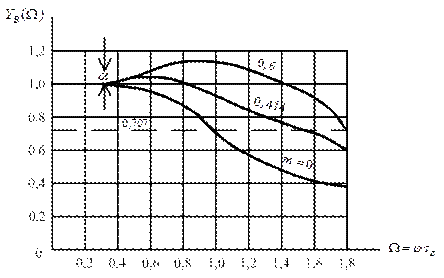
Рисунок 8.7 – АЧХ каскаду для значень m

Користуючись ними неважко побачити на скільки розширює смугу резисторного каскаду введення корекції, чому дорівнює підйом і т.і. Звичайно, смуга оцінюється на рівні 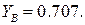Тоді для 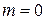маєм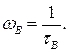о Якщо 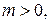гранична частота збільшується до значення Відношення показує у скільки разів розширюється смуга каскаду з корекцією. Залежність 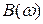подана на рис. 8.8.

Ці графіки побудовані при використанні (8.8) і дозволяють знайти величину підйому частотної характеристики 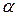та безрозмірну частоту 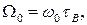на якій спостерігається цей підйом. Як можна бачити з графіків, розширення смуги при 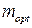складає 1,73. Подальший зріст m збільшує смугу незначно, максимальне розширення складає приблизно 1.82. Підйом частотної характеристики можна використати для компенсації спадання АЧХ попереднього або наступного каскаду.

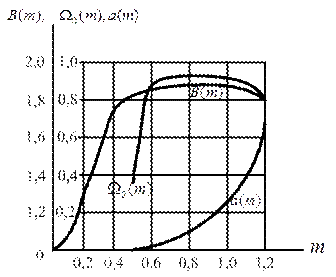
Рисунок 8.8 – Графіки розширення смуги каскаду з корекцією

Площа підсилення каскаду з корекцією

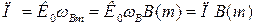
збільшується у 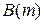разів.

Це збільшення площі можна використати або для розширення смуги частот, або для підвищення підсилення. У першому випадку за вибраним значенням 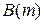на рис. 8.8 знаходять m і зберігають без зміни навантаження 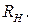Тоді смуга каскаду розширюється у 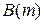разів, а потрібна для корекції індуктивність дорівнює 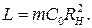У другому випадку за вибраним значенням 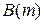знаходять m і, збільшивши навантаження до 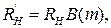одержують підсилення 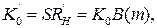тобто у 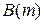разів більше. При цьому смуга частот зберігається без змін, тому що

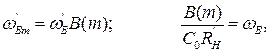
а необхідна індуктивність коректування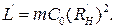

Аналіз показує, що при збереженні повної ємності каскаду 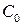(для польового транзистора) без змін, ніякими ускладненнями навантаження неможливо розширити смугу частот більше, ніж у 2 рази. Для каскадів на біполярних транзисторах цього о6меження немає, бо для них крутість та ємність, що шунтує навантаження, не лишаються постійними, а зменшуються з частотою. Отже, навіть така проста двополюсна корекція за допомогою тільки індуктивності дає результат, що мало відрізняється від граничного. Це свідчить про високу ефективність схеми і зумовлює її широке застосування.

Поряд з паралельною індуктивною ВЧ корекцією знаходить своє застосування і послідовна індуктивна ВЧ корекція, рис. 8.7.

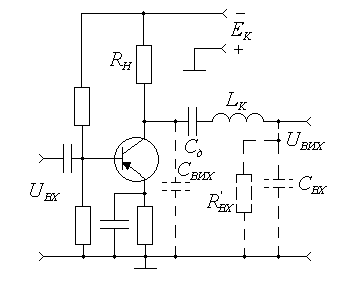
Рисунок 8.9 – Послідовна індуктивна ВЧ корекція

В цьому випадку індуктивність коректування включається послідовно з розділовою ємністю. Еквівалентна схема каскаду з такою корекцією наведена на рис. 8.10.

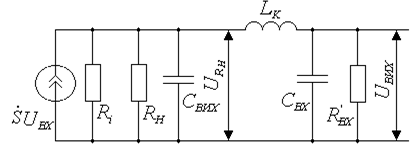
Рисунок 8.10 – Еквівалентна схема каскаду з послідовною індуктивною ВЧ корекцією

Повна паразитна ємність 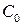при такому включенні індуктивності коректування поділяється на дві частини 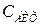і 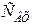, у результаті чого загальна паразитна ємність дорівнює

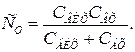
Паралельний резонансний контур, що утворюється 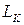і 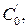має резонансну частоту

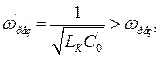
тобто ця частота вище, ніж в схемі з паралельною ВЧ корекцією (якщо значення 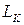однакові).

На частоті 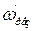опір навантаження каскаду є опором паралельного контуру ІІІ виду, який частково шунтується опорами 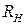і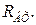

Визначимо опір навантаження каскаду на резонансній частоті 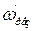. Враховуючи, що 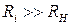і 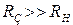(для ПТ), то шунтувальною дією 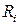i 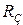на еквівалентний резонансний опір контуру можна знехтувати. В цьому випадку

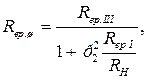
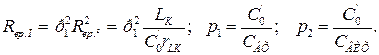
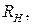Оскільки паралельно частині контуру підключено опір то величина і викиду АЧХ на частоті паралельного резонансу 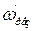не спостерігається, але викид АЧХ може спостерігатися на частоті послідовного резонансу 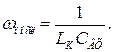Оскільки контур ІІІ виду має три реактивності і напруга виходу знімається з реактивного елемента 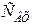(напруга збудження цього контуру 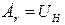) послідовного контуру 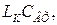то вихідна напруга 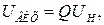і відповідно коефіцієнт підсилення на частоті 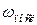може бути більшим за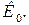

Для більш ефективного згладжування АЧХ часто застосовують опір шунтування 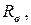що підключається паралельно до індуктивності коректування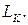

Застосовуючи сполучення схем паралельної і послідовної ВЧ корекціі (складна корекція), можна досягнути більш широкої смуги пропускання і рівномірності коефіцієнта підсилення у досить широкій смузі.