Методи визначення параметрів, що забезпечують рівномірність АЧХ та лінійність ФЧХ у найбільшій області частот

Метод визначення параметрів схеми корекції, що забезпечує рівномірність АЧХ у найбільшій області частот, запропонований Г.В. Брауде. Згідно з цим методом, частотна характеристика може бути подана у вигляді ряду Маклорена

Перший член ряду характеризує ідеальну АЧХ, а решта – відхилення реальної характеристики від ідеальної. Якщо підібрати параметри кола таким чином, щоб

тоді реальна характеристика буде тим ближче до ідеальної, чим більше число похідних буде перетворюватися у нуль. Кількість обернутих у нуль членів ряду визначається кількістю незалежних параметрів кола, що підлягає регулюванню.

Звичайно, на практиці простіше оперувати не , а з виразом для виконуючи розвинення по та подаючи частотну характеристику коефіцієнта передачі чотириполюсника відношенням двох поліномів

(8.1)

Якщo зрівняти члени однакових степенів з лівого та правого боків виразу (8.1), то враховуючи, що дістанемо

За умов корекції необхідно мати Для цього необхідно, щоб Для того, щоб похідні вищих степенів дорівнювали нулю, необхідне виконання умови

(8.2)

Умови фазової корекції знаходяться аналогічно, якщо розглядати час запізнювання (ГЧЗ) та забезпечити його найменшу залежність від частоти. Лінійній ділянці фазової характеристики відповідає незалежне від частоти запізнювання. Чим ширша область частот, у який тим у більш широкій області частот забезпечується лінійна фазова характеристика.

Якщо

Тоді умова фазової корекції має вигляд

(8.3)

Співвідношення (8.2) та (8.3) дозволяють обрати параметри елементів, що забезпечать корекцію АЧХ та ФЧХ. Чим більше похідних можна обернути у нуль, при відповідному виборі параметрів, тим у більшому діапазоні частот АЧХ та ФЧХ буде менше відрізнятися від ідеальної.

Коефіцієнти 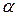та 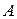по–різному залежать від елементів L, C, R коректованого каскаду, тому умови корекції частотної та фазової характеристик не збігаються.

Досить часто

чисельник функції є виродженим поліномом у якого всі Тоді умова частотної корекції приймає вигляд

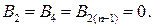(8.4)

Окремий випадок корекції за (8.4), коли всі коефіцієнти полінома 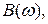крім останнього вдається перетворити у нуль, зветься корекцією за Баттервортом. Йому відповідає характеристика

(8.5)

Частотні характеристики для різних n, що побудовані на підставі (8.5), зображені на рис. 8.1.

Чим вище степінь n поліному, що відображує частотну характеристику, тим ефективніше результат корекції за Баттервортом. 3і зростанням n у межах смуги пропускання підсилення все менше змінюється з частотою, а за її межами різче спадає до нуля.

Вираз (8.5) використовується для математичного опису реальних частотних характеристик. Таку операцію називають апроксимацією характеристик за Баттервортом. Квадрат модуля комплексної функції можна подати у вигляді

Рисунок 8.1 – Частотні характеристики для різних n

Тоді переходячи від до комплексної змінної р, отримаємо для (8.5)