Изображение плоскости

Плоскость в проекциях с числовыми отметками изображается и задается теми же определителями, что и в ортогональных проекциях, а именно:

· тремя точками, не лежащими на одной прямой (рис. 117);

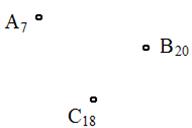Рис. 117

· прямой и точкой, не лежащей на этой прямой (рис. 118);

Рис. 118

· двумя параллельными или пересекающимися прямыми (чертежи см. выше);

· проекциями плоской фигуры (рис. 119).

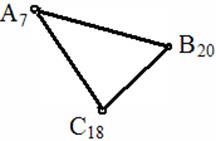Рис. 119

Но обычно в проекциях с числовыми отметками плоскость задается м асштабом уклона ∑ i – это проградуированная проекция линии наибольшего ската плоскости. Его выделяют 2-мя параллельными прямыми (тонкой и толстой) и обозначают буквой с индексом ∑i.

Итак, на рис. 120 изображена плоскость ∑, пересекающая плоскость уровня П0 по линии ∑0. В плоскости ∑ проведена линия ската MN и построена ее проекция mn на плоскость П0. Угол φ между прямой MN и ее проекцией mn определяет угол наклона плоскости ∑ к плоскости уровня П0.

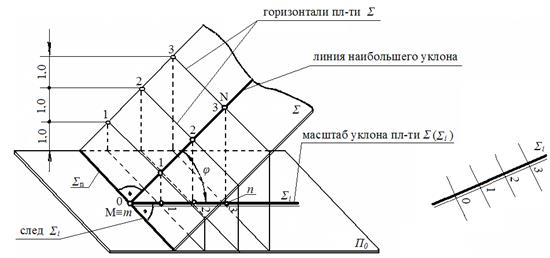
Рис. 120

Проградуируем линию ската по высоте, для этого проведем горизонтальные линии, которые должны быть перпендикулярны к линии ската M N.

Спроецируем горизонтали на проекцию mn, они должны быть параллельны следу ∑0.

Итак, плоскость ∑ задана на чертеже масштабом уклонов ∑i, которая, как говорилось выше, изображается в виде 2-х параллельных прямых, одна из которых в 2-3 раза толще другой, и горизонталей, перпендикулярных к масштабу уклонов.

Проекция mn линии ската MN с нанесенными на ней

интервалами является масштабом уклона плоскости ∑ и обозначается, в данном случае, ∑i.

Углом падения плоскости ∑ называют угол j, образованный данной плоскостью ∑ и плоскостью П0.

Иногда, особенно при решении инженерных задач на местности,

требуется определить положение плоскости по отношению к сторонам света. В таком случае вводится понятие угла простирания плоскости.

Под направлением простирания принимают правое направление горизонталей, если смотреть на плоскость в сторону возрастания числовых отметок.

Угол, составленный земным меридианом и направлением простирания называется углом простирания (ψ) и является азимутом этих линий. Этот угол отсчитывается от северного конца меридиана против часовой стрелки до направления простирания.

Углы падения и простирания находят широкое применение в геологии как элементы, характеризующие залегание пласта горной

породы в толще земной коры.

Задача1. Через точку А7 провести плоскость ∑ с углом падения

j = 350 и углом простирания ψ = 1350(рис. 121).

Решение:

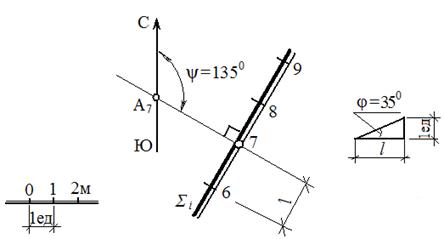
Рис. 121

Вершиной угла простирания может быть любая точка чертежа, в том числе и точка А. Через проекцию А7 данной точки проведем земной меридиан «север – юг» и под углом ψ = 1350– прямую линию (направление простирания), которая будет являться горизонталью искомой плоскости, имеющей отметку 7. В произвольном месте под прямым углом к этой горизонтали проведем линию масштаба уклонов

искомой плоскости ∑i. Для градуирования масштаба уклонов, т. е. для определения интервала ℓ плоскости, построим прямоугольный треугольник с одним катетом, равным единице длины (заданного масштаба) и противолежащим углом j = 350. Второй катет этого треугольника и будет являться интервалом ℓ.

Или рассчитать по формуле: LР= 1 / tg j.

При градуировании масштаба уклонов принято, что возрастание

отметок идет от наблюдателя вперед вытянутой в сторону правой руки, совпадающей с направлением простирания.