Маршрутная перестановка

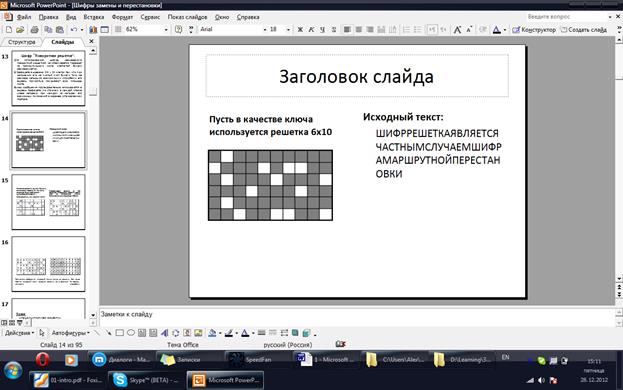
Преобразования из этого шифра состоят в том, что в фигуру исходный текст вписывается по ходу одного ``маршрута'', а затем по ходу другого выписывается с нее. Такой шифр называют маршрутной перестановкой.

Например, можно вписывать исходное сообщение в прямоугольную таблицу, выбрав такой маршрут: по горизонтали, начиная с левого верхнего угла поочередно слева направо и справа налево.

Выписывать сообщение будем по другому маршруту: по вертикали, начиная с верхнего правого угла и двигаясь поочередно сверху вниз и снизу вверх.

При расшифровании надо определить число длинных столбцов, т.е. число букв в последней строке прямоугольника. Для этого нужно разделить число буев в сообщении на длину числового ключа. Остаток от деления и будет искомым числом.

Шифр ``Сцитала''.

Одним из самых первых шифровальных приспособлений был жезл (``Сцитала''), применявшийся еще во времена войны Спарты против Афин в V веке до н. э.

Это был цилиндр, на который виток к витку наматывалась узкая папирусная лента (без просветов и нахлестов), а затем на этой ленте вдоль его оси записывался необходимый для передачи текст. Лента сматывалась с цилиндра и отправлялась адресату, который, имея цилиндр точно такого же диаметра, наматывал ленту на него и прочитывал сообщение. Ясно, что такой способ шифрования осуществляет перестановку местами букв сообщения.

Шифр ``Сцитала'‘ реализует не более n перестановок (n - длина сообщения).

Действительно, этот шифр, как нетрудно видеть, эквивалентен следующему шифру маршрутной перестановки: в таблицу, состоящую из столбцов, построчно записывают сообщение, после чего выписывают буквы по столбцам. Число задействованных столбцов таблицы не может превосходить длины сообщения.

Имеются еще и чисто физические ограничения, накладываемые реализацией шифра ``Сцитала''. Естественно предположить, что диаметр жезла не должен превосходить 10 сантиметров. При высоте строки в 1 сантиметр на одном витке такого жезла уместится не более 32 букв (10p < 32). Таким образом, число перестановок, реализуемых ``Сциталой'', вряд ли превосходит 32.

Шифр ``Поворотная решетка''.

Для использования шифра, называемого поворотной решеткой, изготавливается трафарет из прямоугольного листа клетчатой бумаги размера клеток.

В трафарете вырезано 2 m x 2 k клеток так, что при наложении его на чистый лист бумаги того же размера четырьмя возможными способами его вырезы полностью покрывают всю площадь листа.

Буквы сообщения последовательно вписываются в вырезы трафарета (по строкам, в каждой строке слева направо) при каждом из четырех его возможных положений в заранее установленном порядке.

1. Шифры замены. Математическая модель. Примеры.

• Поточные шифры (Цезаря)

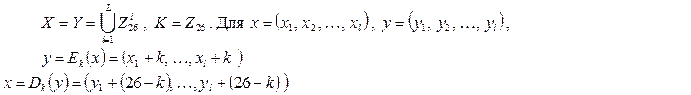
• Блочные шифры (Порта и Пфейфера)

Основа – прямоугольная таблица, в которую записан систематически перемешанный алфавит.

Правило зашифрования:

Буквы биграммы (i, j), i ¹ j, находятся в данной таблицк. При зашифровании биграмма (i, j) заменяется биграммой (k, l), где определяются с правилами:

1. Если i и j не лежат в одной строке или одном столбце, то их позиции образуют противоположные вершины прямоугольника. Тогда k и l – другая пара вершин, причем k –вершина, лежащая в той же строке, что и i.
2. Если i и j лежат в одной строке, то k и l – буквы той же строки, расположенные непосредственно справа от i и j соответственно. При этом если одна из букв – последняя в строке, то считается, что ее «правым соседом» является первая буква той же строки.
3. Аналогично если i и j лежат в одном столбце, то они заменяются «соседями снизу.»

Пример шифра Плейфера.

Пусть шифр использует прямоугольник 5х6, в который записан систематически перемешанный русский 30-буквенный алфавит на основе ключевого слова «командир».

к	о	м	а	н	д
и	р	б	в	г	е
ж	з	л	п	с	т
у	ф	х	ц	ч	ш
щ	ь	ы	э	ю	я

Зашифруем фразу

«автором метода является Уитстон».

В качестве «пустышки» будем использовать редкую букву ф.

Представим фразу в виде последовательности биграмм:

АВ ТО РО МФ МЕ ТО ДА ЯВ ЛЯ ЕТ СЯ УИ ТС ТО НФ

Шифртекст:

ВП ЗД ЗР ОХ ДБ ЗД КН ЭЕ ТЫ ТШ ШД ЩЖ ЖТ ЗД ОЧ

Криптоанализ шифра Плейфера опирается на частотный анализ биграмм, триграмм и четырехграмм шифртекста и особенности замены шифрвеличин на шифрообозначения, связанные с расположением алфавита в прямоугольнике.

Существенную информацию о заменах дает знание того, что используется систематически перемешанный алфавит.

1. Шифры перестановки. Математическая модель. Примеры.

Шифр, преобразования из которого изменяют только порядок следования символов исходного текста, но не изменяют их самих, называется шифром перестановки.

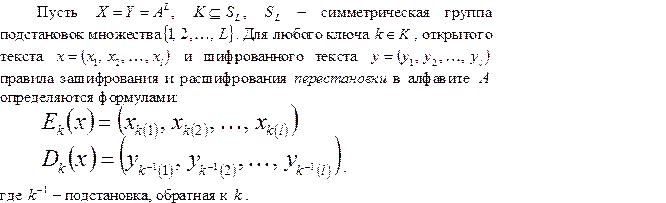
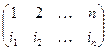Пример
Рассмотрим, предназначенное для зашифрования сообщения длиной n символов. Его можно представить с помощью таблицы

где i1 - номер места шифртекста, на которое попадает первая буква исходного сообщения при выбранном преобразовании, i2 - номер места для второй буквы и т.д.

В верхней строке таблицы выписаны по порядку числа от 1 до, а в нижней - те же числа, но в произвольном порядке. Такая таблица называется подстановкой степени n. Зная подстановку, задающую преобразование, можно осуществить как зашифрование, так и расшифрование текста.

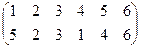Зная подстановку, задающую преобразование, можно осуществить как зашифрование, так и расшифрование текста. Например, если для преобразования используется подстановка

и в соответствии с ней зашифровывается слово МОСКВА,

то получится КОСВМА.

Число различных преобразований шифра перестановки, предназначенного для зашифрования сообщений длины n, меньше либо равно n! (в это число входит и вариант преобразования, оставляющий все символы на своих местах!).

1. Шифры гаммирования. Математическая модель. Примеры.

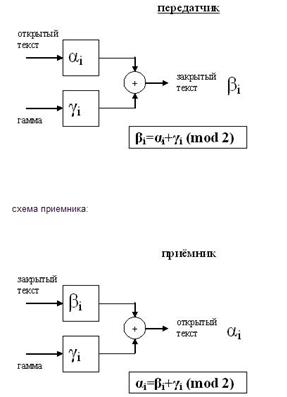
Гамми́рование — симметричный метод шифрования, основанный на «наложении» гамма-последовательности на открытый текст. Обычно это суммирование в каком-либо конечном поле

Принцип шифрования заключается в формировании генератором псевдослучайных чисел (ГПСЧ) гаммы шифра и наложении этой гаммы на открытые данные обратимым образом, например путем сложения по модулю два. Процесс дешифрования данных сводится к повторной генерации гаммы шифра и наложении гаммы на зашифрованные данные. Ключом шифрования в данном случае является начальное состояние генератора псевдослучайных чисел. При одном и том же начальном состоянии ГПСЧ будет формировать одни и те же псевдослучайные последовательности.

1. Принципы построения блочных шифров. Схема Фейстеля.

Сеть Фейстеля:

Сеть Фейстеля — это общий метод преобразования произвольной функции F в перестановку на множестве блоков. ^[15] Она состоит из циклически повторяющихся ячеек — раундов. Внутри каждого раунда блок открытого текста разделяется на две равные части. Раундовая функция

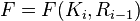
берет одну половину (на рис. правую), преобразует её с использованием ключа K_i и объединяет результат с второй половиной посредством операции исключающее ИЛИ (XOR). Этот ключ задаётся первоначальным ключом K и различен для каждого раунда. Далее половинки меняются местами (иначе будет преобразовываться только одна половина блока) и подаются на следующий раунд. Преобразование сети Фейстеля является обратимой операцией.

Для функции F существуют определенные требования:

· её работа должна приводить к лавинному эффекту

· должна быть нелинейна по отношению к операции XOR

В случае невыполнения первого требования, сеть будет подвержена дифференциальным атакам (похожие сообщения будут иметь похожие шифры). Во втором случае действия шифра линейны и для взлома достаточно решения системы линейных уравнений. ^[3]